2020-03-28

개념 정리

LU Decomposition

LU Decomposition

지금까지 선형방정식을 풀었던 방식은

 

1. 가우스-조르단 소거법을 이용

     : 첨가행렬을 기약행사다리꼴까지 변형시킨 후 선행변수를

       자유변수로 표현

 

2. 가우스 소거법 + 역대입법을 이용

     : 첨가행렬을 행사다리꼴까지 변형시킨 후 선행변수를

       자유변수로 표현

LU Decomposition

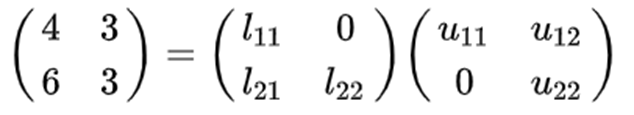
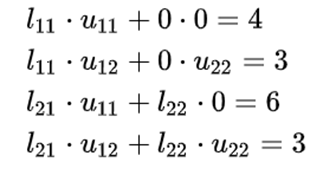
LU 분해(LU decomposition)는 수치 해석 분야에서 하삼각행렬과 상삼각행렬의 곱으로 표현하는 것이다. L과 U는 각각 Lower와 Upper를 의미한다 - 위키백과

LU Decomposition

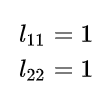
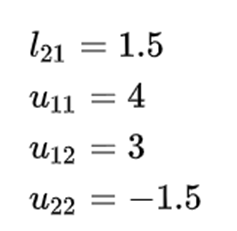
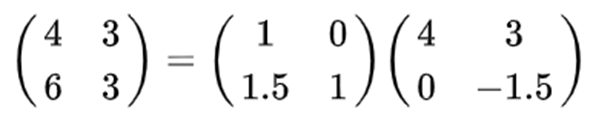
하삼각행렬 L의 대각성분을 1로 두자.

참고로, 하삼각행렬과 상삼각행렬의 행렬식은 대각성분의 곱이다.

LU Decomposition

LU 분해의 목적은?

Decomposition(분해)는 어떤 시스템 혹은 데이터를 표현한 행렬 A를 '인수 분해' 한다는 뜻이다.

 

선형대수에서 행렬 분해는 어떤 행렬을 여러 행렬들의 곱으로 표현하는 것을 의미한다. 중학교때 배웠던 인수 분해를 하는 이유와 같은 맥락으로 방정식의 해를 구하기 위해서이다.

 

즉, 계산의 편리함과 분석적 용이성을 위함이다.

 

행렬 분해는 SVD, QR 분해 등이 있고, 기본적인 형태가 LU 분해다.

LU Decomposition

LU 분해를 어떻게 하는 지 알기 전에!

 

어떻게 활용하는지 알아봅시다!

LU Decomposition

LU 분해로 행렬식 구하기

정방행렬 A=LU로 분해되어 있으면,

 

행렬식의 성질에 따라, '곱의 행렬식은 행렬식의 곱' 이므로

 

det A = det (LU) = (det L)(det U) 가 된다.

 

하삼각행렬이나 상삼각행렬의 행렬식은 대각성분의 곱이므로

 

det L = 1이고,

det A = 1 x (U의 대각성분의 곱) 이 된다.

LU Decomposition

LU 분해로 일차방정식 구하기

Ax = y가 되는 x를 구해봅시다.

 

우선, A를 LU 분해를 한다.                                             [1]

그러면, Ax = (LU)x가 되고, x에 U를 곱하고 거기에 L을 곱한다.

 

즉, (LU)x = L(Ux) = Lz = y 가 된다(Ux는 z로 치환).

 

                                            [3]

 

                      [2]

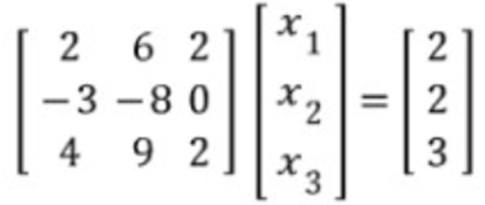
LU Decomposition

LU 분해로 일차방정식 구하기

[1] 

 

 

 

[2]   

 

 

 

[3] 

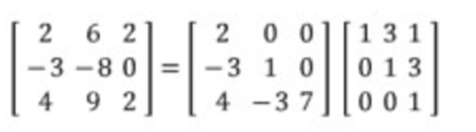
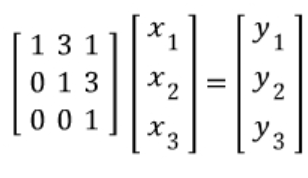
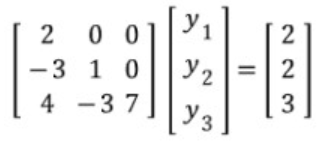
Z

LU Decomposition

LU 분해로 역행렬 구하기

역행렬은 AB = I의 과계식을 가진다.

A의 역행렬을 LU 분해로 구하기 위해서, A를 LU 분해한다.

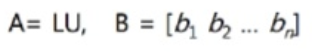
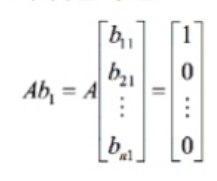
B의 첫 번째 행 계산

B의 두 번째 행 계산

B의 마지막 행 계산

...

LU Decomposition

LU 분해로 역행렬 구하기

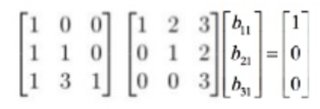
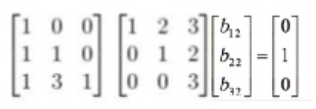
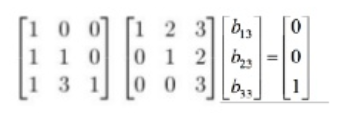
A

B = I

3개의 변수,

3개의 연립방정식

LU Decomposition

이제 LU 분해를 어떻게 하는 지 알아보자.

LU Decomposition

A = \begin{bmatrix} 2 & 1 \\ 8 & 7 \end{bmatrix}

에서 상삼각행렬 U를 구해보자.

상삼각행렬을 만들기 위해선

\begin{bmatrix} x & y \\ 0 & z \end{bmatrix}

과 같은 꼴로

만들어주어야 하기 때문에 가우스 소거법을 이용한다.

U = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}

가우스 소거법으로

이 되고,

E_{21} \times A = U
E_{21} = \begin{bmatrix} 1 & 0 \\ -4 & 1 \end{bmatrix}
L = \begin{bmatrix} 1 & 0 \\ 4 & 1 \end{bmatrix}

이므로,

이 된다.

여기서                      가 되므로,       의 역행렬이 곧 L이 된다.

A = E_{21}^{-1} \times U
E_{21}

즉,                     이 된다.

잘 생각해보면, 가우스 소거법을

이용해 L과 U를 한 번에 구할 수 있다.

다음 시간에

파이썬으로 행렬식, 일차방정식, 역행렬을 각각 가우스-조르단과

LU 분해로 구해서 시간복잡도를 비교해보자.