07/05
지 명 화
분산분석
이상철 교수님의 빅데이터 통계학
분산분석(analysis of variance, ANOVA)
- 영국의 통계학자인 피셔에 의해 개발
- 세 그룹 이상의 분산을 검정하여, 각 집단의 모평균 차이를 비교 검정
- 기존에 알려진 T-test(T-분포)와는 다른 분포(F-분포)를 사용해서 집단을 비교
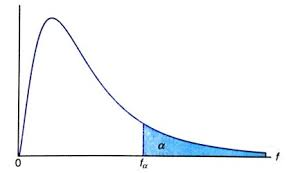
- 분산에 영향을 주는 변수를 몇 개의 수준(level)으로 나누어서 대상에게 실험한다.
- 종류: 일원분산분석(one-way ANOVA), 이원분산분석(two-way ANOVA), 다원변량분산분석(MANOVA), 공분산분석(ANCOVA)
요인과 수준(level)
예시) 치킨의 맛을 결정하는 온도는?
- 반응값(특성치): 치킨 맛
- 요인: 튀기는 온도
- 수준 수: 4(200도, 250도, 300도, 350도)
- 고정효과모형(fixed effect model): 요인을 실험자가 선택
- 변량효과모형(random effect model): 요인을 무작위로 선택
- 혼합모형(mixed effect model): 두 개의 요인 중 하나는 실험자가 하나는 무작위로 선택
요인 수준 선택에 따른 ANOVA 종류
예시) K 레스토랑은 서울에 10개의 매장을 가지고 있다.
- 강남, 강서, 강동, 강북 지역의 4개의 매장에 대한 만족도 차이를 보고 싶다. -> 고정효과모형
- 10개의 매장 중 4개의 매장을 임의로 선택해서 K 레스토랑의 전체 만족도의 차이를 보고 싶다. -> 변량효과모형
- 매장 간에는 메뉴가 서로 다양하다. 강남, 강서, 강동, 강북 4개의 매장을 설정하고, 메뉴는 임의로 3개씩 선택한다. -> 혼합모형
- t-test로 여러 번 중복해서 비교할 수록 신뢰도가 하락한다.
- 예를 들어, t-test 알파 0.05로 비교실험을 했을 때, 신뢰도는 (1-a)이다. 이러한 실험을 두 번 반복하는 경우, 동시에 일어나는 사건이므로 곱셈으로 처리해서 신뢰도가 제곱이 된다. 즉, 한 번 비교했을 때보다 신뢰도가 감소한다. 따라서 n번 반복할 수록 신뢰도가 감소하고, n이 무한대로 갈수록 신뢰도가 0이 된다.
- 반면에, f-test 알파 0.05의 경우 집단간의 비교 검정이 한 번만 일어나서 신뢰도는 (1-a)가 된다.
왜 T-test를 여러 번 사용해서 비교분석하지 않고, ANOVA 테스트를 하는걸까?
일원분산분석(one-way ANOVA)
- 언제 사용하는가? [예시 1] 체중 감소에 차(tea)의 종류가 미치는 영향을 연구할 때 차를 녹차, 홍차, 물로 나누는 경우 [예시 2] 체중에 따른 다리 근력을 연구할 때, 참가자를 체중에 따라 비만, 과체중, 정상으로 나누는 경우
- 일원분산분석은 두 독립적인 집단의 평균을 F-분포를 이용해서 비교하는 데 쓴다.
- 가설검정의 귀무가설은 두 평균이 같다.
- 한계점은? 일원분산분석은 최소한 두 가지 집단에 대해서 이들이 서로 다른지를 알려준다. 하지만 어떤 그룹이 다른지를 알려주지 않는다. 만약 F-통계량이 유의미한 값을 반환한다면, 어떤 그룹이 다른 평균값을 가지는지 최소 유의적 차이 검정(LSD) 등과 같은 추가적인 검정을 시행해야 한다.
이원분산분석(two-way ANOVA)
- [예시] 월급과 성별이 이직할 때의 면접에서 긴장(nervous) 정도에 영향을 끼치는 지 알고 싶을 때. 긴장 정도가 결과값(측정변수), 성별과 월급이 두 가지 범주형 변수이다. 이 범주형 변수들은 이원분산분석에서 요인이라고 부르는 독립변수이다. 또한, 이 요인은 수준(level)로 나눌 수 있다. 월급 수준은 낮음/보통/높음으로, 성별은 남성/여성/젠더로 나눌 수 있어서 총 9개의 대상 집단이 있다.
- 이원분산분석은 일원분산분석을 확장한 것으로, 두 개의 범주형 설명변수가 있고, 그 결과값이 측정가능한 변수를 가질 때 사용한다.
- 주효과(Main Effect): 각 요인의 효과는 개별적으로 고려된다.
- 교호작용효과(Interaction Effect): 모든 요인들이 동시에 고려된다.