06/20

지 명 화

표집분포와 통계적 추론

이상철 교수님의 빅데이터  통계학

통계적 추론의 흐름

  • 표본조사를 하는 이유는?  모집단의 값을 추론하기 위한 것이 통계적 추론, 하지만 전수조사를 할 수 없기 때문에 표본조사를 함.
  • 표본을 추출하기 위해서 범주형 데이터와 수치형 데이터를 가져옴.
  • 가져온 데이터를 정리하는 기술통계학
  • 오차범위를 추정하기 위해 필요한 확률

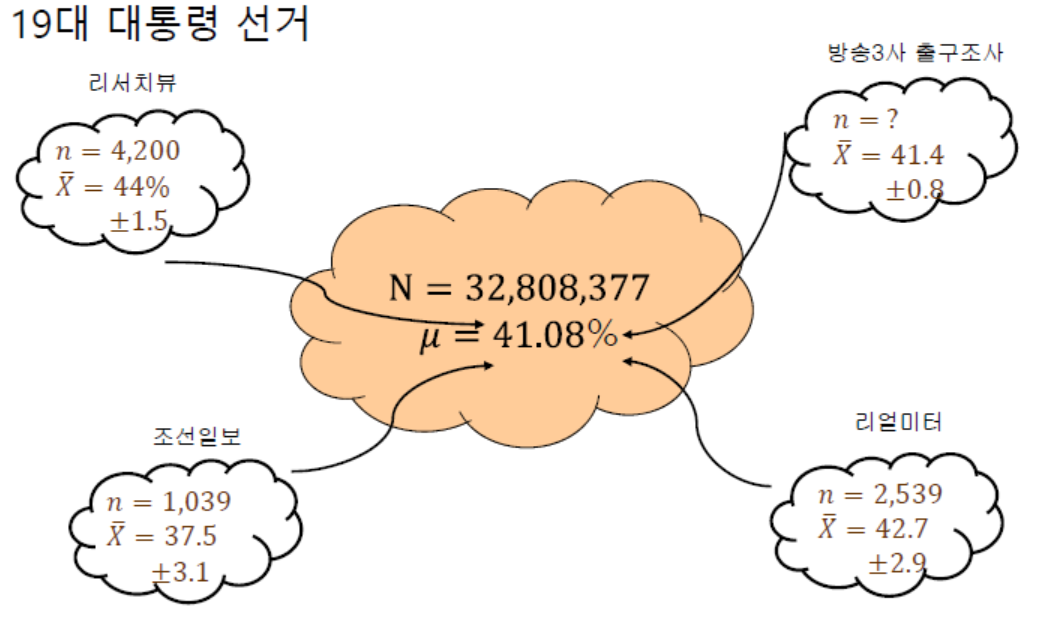
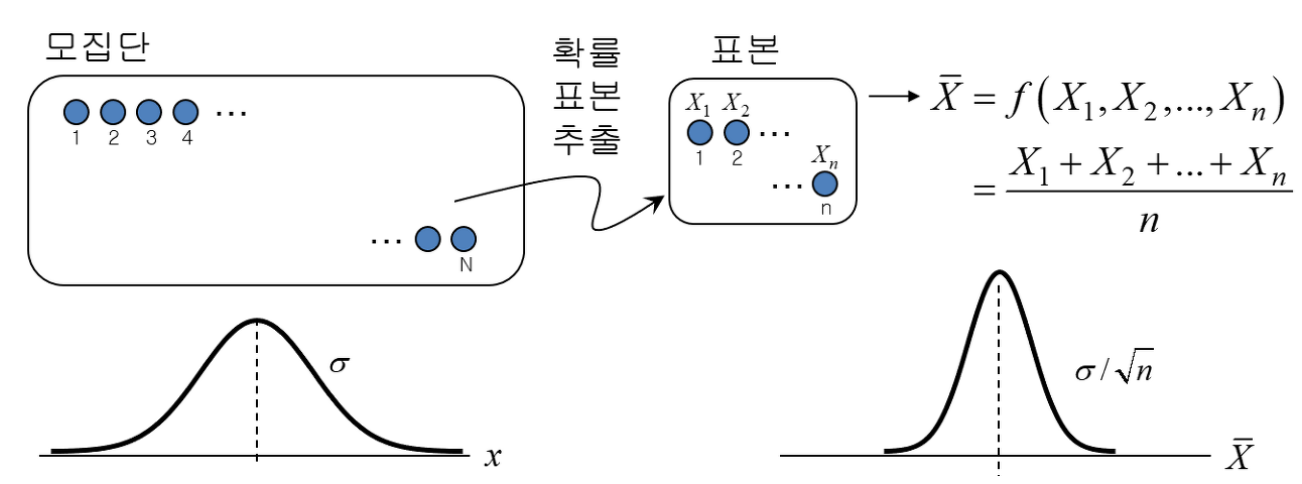
표집분포(Sampling Distribution)

  • 예전에는 표본분포라고 불렸음
  • 모집단에서 추출한 표본크기 n개의 추정치의 확률분포
  • 모집단에서 일정한 크기(n)로 표본을 모두(k개)로 뽑아서 각 표본의 평균을 계산하였을 때, 그 표본의 평균의 확률분포
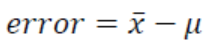
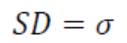
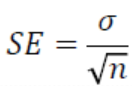
  • 표본오차(samplling error): 모집단의 값과 표본의 값에서 발생하는 차이
  • 표준편차(standard deviation): 자료의 산포도를 나타내는 수치로, 모집단에 속한 다른 숫자들이 모평균과 차이나는 평균적인 정도. 즉, 한 집단의 숫자들이 평균을 중심으로 퍼진 정도
  • 표준오차(standard error): 통계의 표본평균의 표준편차로 각 표본들의 평균이 전체 평균과 얼마나 떨어져 있는지를 보여줌. 평균의 정확도(추정값인 표본평균들과 참값인 모평균과의 표준적인 차이)

주요 용어

표준오차

  • 표본을 뽑을 때마다 모집단과 차이가 발생
  • 한 번 뽑을 때보다 여러 번 뽑을 때의 오차 범위가 작아짐

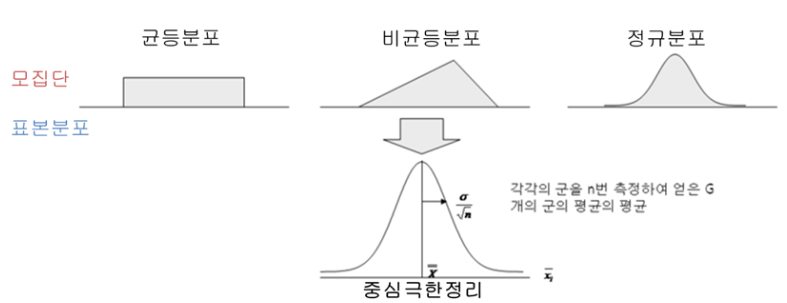
중심극한 정리(Central limit theorem)

  • 평균이 𝛍이고 표준편차가 𝝈인 모집단으로부터 추출된 표본의 개수가 n개라면, 표본의 표집분포는 평균이 𝛍이고 분산이 𝝈𝟐/𝒏인 정규분포에 근사한다.
  • n이 커질수록(보통 30 이상) 모집단의 형태와 상관없이 표집분포는 정규분포에 근사

https://drhongdatanote.tistory.com/57

  • 중심극한의 정리가 중요한 이유는 표본 수집을 기반으로 한 추리통계에서 중요한 이론적 근거를 제시하고 있기 때문
  • 모집단이 어떤 분포를 가지고 있던지 간에 일단 표본의 크기가 충분히 크다면, 표본 평균들의 분포가 모집단의 모수를 기반으로 한 정규분포를 이룬다는 점에서, 특정 사건(수집한 표본의 평균)이 일어날 확률값을 계산할 수 있다는 것
  • 중심극한정리는 표본 평균들이 이루는 표본 분포의 모집단간의 관계를 증명함으로써, 수집한 표본의 통계량을 이용해 모집단의 모수를 추정할 수 있는 수학적(확률적) 근거를 마련해줌.

통계적 추론

  • 통계적 추론이란
  • 관심대상인 모집단의 특성을 파악하기 위해 모집단으로부터 관련된 일부 자료(표본)을 수집하고
  • 수집된 표본의 자료를 요약하여 표본의 특성을 파악하고
  • 표본의 자료를 이용하여 모집단의 특성에 대해 확률을 이용해 추론
  1. 추정(모집단이 얼마인지 예측하는 것)
  2. 가설검정(모집단이 이것이다 아니다라고 결정하는 것)

통계적 추론의 종류

추정

  • 표본의 평균과 표준오차(SE)를 구해서 모수의 범위를 구하는 것
  • 신뢰구간의 일정한 확률범위 내에서 모수의 값이 포함될 가능성이 있는 범위
  • 신뢰구간은 90%, 95%, 99%의 확률 값
  • 종류: 점추정, 구간추정

점추정(Point estimation)

  • 모수에 가장 가까우리라고 생각되는 하나의 값으로 모수를 추정
  • 모집단으로부터 표본을 추출하고, 추출된 표본의 통계량{표본평균, 표본표준편차}을 통해 모수{모평균, 모표준편차}를 추정할 때 사용

점추정 방법

  1. 적률법(method of moments): 기대값 이용
  2. 최대가능도(우도)추정법(maximum likelihood estimation): 조건부 확률
  3. 최소제곱법(least squares estimation): 회귀분석에서 사용

구간추정(Interval estimation)

  • 점추정만으로는 모수가 얼마나 정확하게 추정되었는지 알 수 없으므로, 모평균이 존재할 구간을 확률적으로 추정하는 방법
  • 신뢰구간(confidence interval, CI)을 이용

신뢰구간

  • 연속형 자료의 경우 표본의 크기가 충분히 크다면, 중심극한정리에 의해 표본 평균이 정규분포를 따른다고 가정할 수 있다.
  • 정규분포라는 가정 하에 표본 평균과 표본 표준편차로부터 모평균의 신뢰구간을 구할 수 있다.

https://dermabae.tistory.com/184

  • 표본의 수(n)가 클수록 모평균은 정밀하게 추정될 수 있지만, 표본의 수(n)가 작다면 신뢰구간이 너무 넓어 모평균이 실제로 어디쯤에 위치할지 예측하기 어렵다.
  • 신뢰구간의 95%라는 것은 100개의 표본 중, 95개는 모수의 평균값이 들어가있다는 것을 말함.

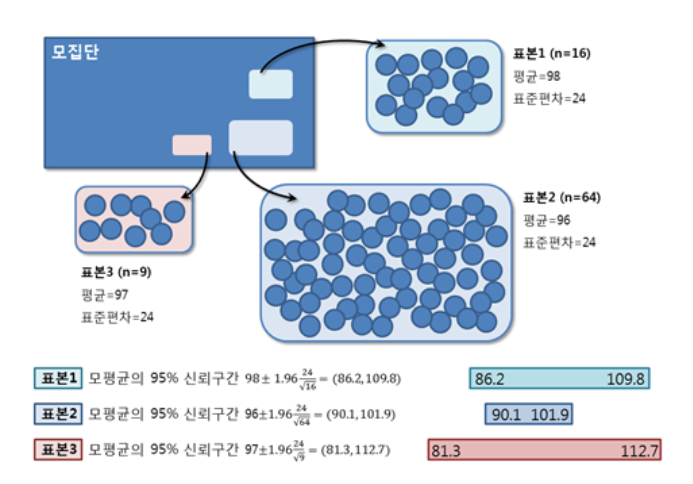
그렇다면 신뢰구간이 99%가 가장 좋은 것은 아닌가??

  • 99%의 신뢰구간은 신뢰도가 굉장히 높은 구간이기에, 신뢰도를 높이기 위해서는 구간의 길이가 길어진다(구간의 길이가 길수록, 모수가 구간 안에 포함될 확률은 높아지므로).
  • 반대로 10%의 신뢰구간은 신뢰도가 굉장히 낮은 구간인데, 구간의 길이가 짧을수록 신뢰도는 낮아진다(구간의 길이가 짧을수록, 모수가 구간 안에 포함될 확률은 낮아지므로).
  • 하지만, 꼭 구간의 길이기 길어서 신뢰도가 높은 것이 무조건 좋다고 할 수는 없다. 왜냐하면 구간의 길이가 길어질수록 최종적으로 모수를 추리하기가 애매해진다. 예를 들어, 구간의 길이가 1<= x <= 3이라고 하면, 모수는 1, 2, 3 중 하나로 추리할 수 있지만, 구간의 길이가 1 <= x <= 12라 하면, 모수는 1~12 중 하나가 되기에 모수를 추리하기가 애매해진다.
  • 따라서 각각의 신뢰구간은 장단점이 있다.
    • 90%: 틀릴확률은 높지만, 모수를 추리하기 편하다.
    • 95%: 일반적
    • 99%: 틀릴확률은 낮지만, 모수를 추리하기 애매하다.