확률 개념과 원리

05/30

지 명 화

  • 통계학에서 연구를 위해 조사가 필요한 경우가 생김
  • 전수조사를 할 수 없다.
  • 표본 조사를 한다.
  • 표본 오차(모집단의 모수를 직접 구할 수 없기 때문에)가 발생한다.
  • 모집단의 모수를 추측할 수 밖에 없다.
  • 오차의 범위를 확률을 통해 구한다.

확률을 배우는 이유는?

개념

  • 전체 중에 이 사건이 가질 수 있는 경우(경우의 수가 필요함)
  • 비슷한 현상이 반복해서 일어날 경우에 어떤 사건이 발생할 가능성을 0과 1사이의 숫자로 표현한 것
  • ex) 로또에 당첨될 확률은?

활용

  • 표본의 자료를 통해서 구한 통계량을 가지고 모집단의 모수를 추정
  • ex) 추정: 신뢰수준(95%)                                    가설검정: 유의수준(5%)

종류

  • 경험적(Empirical)

         - 실험을 통한 확률

         - ex) 흡연자 중 폐암에 걸릴 확률

  • 고전적(Classical)

         - 이론적 확률

         - ex) 주사위에서 1이 나올 확률

  • 주관적(Subjective)

         - 주로 전문가의 의견

         - ex) 새로운 상품이 시장에서 성공할 확률

  • 실험                                                                                                 

      사전에 알려지지 않은 결과를 관찰하는 과정

 

  • 표본공간                                                                                         

      통계적 실험이나 조사에서 일어날 수 있는 모든 가능한 결과의 모임, 주로 S를 사용                     ex)  {구매, 비구매}

 

  • 사건 또는 사상                                                                                

      표본공간에서 결과의 부분 집합

         (이산형) S = { 구매 }

         (연속형) S = {m: m > 0}

확률 용어

1. 계산의 기본 규칙(곱셈의 법칙)

   - 각 실험의 집합: T1, T2, T3, .., Tk

   - 가능한 실험의 결과(수) : n1, n2, n3, ..., nk

   - k번 실험한 결과의 집합 : n1 x n2 x n3 x ... x nk

 

ex) 부사장 3명, 이사 4명, 부장 5명이 있는 회사에서,

      대표 1명씩 총 3명의 위원회가 열릴 경우의 수는?  3 x 4 x 5 = 60

카운팅(경우의 수)의 기본 규칙

2. 부분합의 계산

   - 각 실험의 집합: T1, T2, T3, .., Tk

   - 가능한 실험의 결과(수) : n1, n2, n3, ..., nk

   - k번 실험한 결과의 집합 : n1 x n2 x n3 x ... x nk

 

ex) 부사장 3명, 이사 4명, 부장 5명이 있는 회사에서,

       2명으로 위원회를 구성할 수 있는 경우는?  (3x4) + (3x5) + (4x5) = 12 + 15 + 20 = 47

순열(Permutation)

서로 다른 n개 중 r개를 선택해 순서를 고려해 나열하는 방법의 수

 

ex) 야구경기에는 총 9명의 플레이어가 있으며, 9개의 타순이 있다.

      K 야구 구단 이감독은 9개의 타순을 짜려고 한다. 모든 경우의 수는?

      n! = 9! = 9 x 8 x ... x 1 = 362800

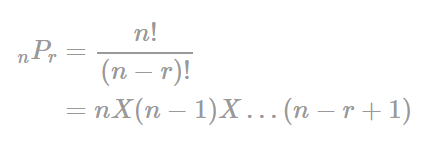
조합(Permutation)

n개 중 r개를 선택해 순서를 고려하지 않고 뽑는 방법의 수

 

ex1) 45개의 번호를 가진 로또에서 6개의 숫자를 고를 경우의 수는?

      45C6 = 45P6 / 6! = 8,145,060

 

ex2) 이 중 6개 중에서 3개의 숫자가 동일할 경우 5등이다. 경우의 수와 확률은?

      6C3 x 39C3 = 20 x 9,139 = 182,780

      182,780 / 8,145,060 = 0.022(2.2%)

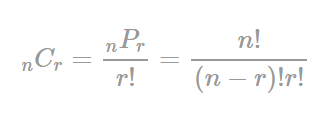
확률과 승산비

승산비: 사건이 발생할 확률과 발생하지 않을 확률간의 비율

 

P(A) / P(A') = P(A) / (1-P(A))     or     P(A') / P(A) = (1-P(A)) / P(A)

 

ex) 승마나 게임에서는 사건 A에 반대하는 승산비로 표시: 4:1

      A 경주마에 대한 승률이 4:1이라고 했을 경우에 승산비와 승률은?

      P(A') / P(A) = (1-(1/5)) / (1/5) = (4/5) / (1/5) = 4

      P(win) = a / (a + b) = 1 / (4 + 1) = 1/ 5 = 0.2

조건부확률

  • A라는 조건이 주어진 상태에서 B가 발생할 확률
  • 교차분석, 데이터 마이닝에서 중요한 개념 -> 연관성 분석

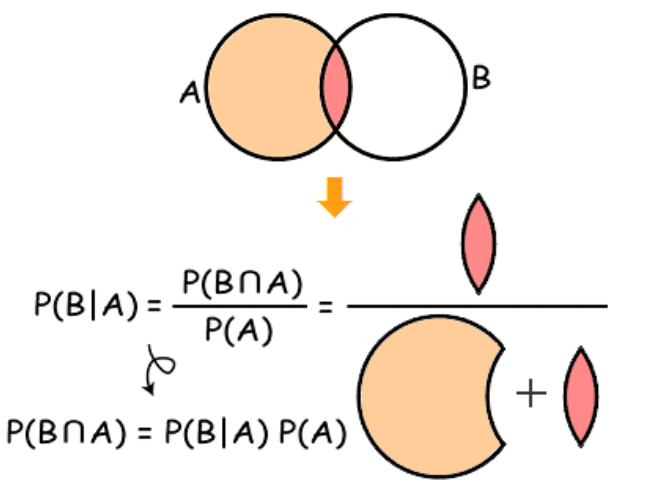
https://m.blog.naver.com/PostView.nhn?blogId=alwaysneoi&logNo=100148922781&proxyReferer=https:%2F%2Fwww.google.com%2F

ex) A 전자는 컴퓨터를 산 사람에게 키보드를 사라고 추천하고 싶다. 과연 컴퓨터를 산 사람에게 키보드를 사라고 추천해도 될까? 기존의 100명을 대상으로 한 판매데이터를 가지고 분석해보자.

  P(컴퓨터) = 60 // 컴퓨터를 살 확률

  P(키보드) = 50 // 키보드를 살 확률

  P(컴퓨터 ∩ 키보드) = 40 // 컴퓨터와 키보드를 모두 살 확률

 

>> 컴퓨터를 산 사람에게 지켜만 보고 그냥 키보드를 팔았을 때(Confidence)

      P(키보드 | 컴퓨터) = P(컴퓨터 ∩ 키보드) / P(컴퓨터) = 40 / 60 = 0.666

 

>> 컴퓨터를 산 사람에게 키보드를 살 것이냐고 직접 물어봤을 때(Lift)

      P(키보드 | 컴퓨터) / P(키보드) = 0.67 / 0.5 = 1.33(확률이 아니라 배)가 높아짐

  • Support (지지율)                                                                                                         

  - P(A) or P(A, B) // A의 확률 or A, B가 일어날 확률, Probably

  - 사건이 일어나는 비율

  - 전체 거래 가운데 A 또는 A, B 모두가 들어있을 비율

  - 지지율 = A, B를 포함한 거래수 / 전체거래수

  • Confidence (신뢰도)                                                                                                   

  - P(B|A) = P(A, B) / P(A)

  - 선행 사건이 일어나고 난 후 후행 사건이 일어날 확률

  - 항목 A가 발생한 상태에서 B가 발생할 확률

  - 1에 가까울 수록 확률이 높다

  • Lift (향상도)                                                                                                                 

  - P(B|A) / P(B)

  - 예측에 있어서 무작위 추측에 비해 규칙이 얼마나 더 우수한가

  - Confidence를 후행사건의 빈도로 나누어 주는 것

베이즈 정리(Baye's Rule)

베이즈 정리: 사전 확률과 사후 확률 사이의 관계를 조건부확률을 이용해서 계산

 

P(A|B) = P(A ∩ B) / P(B) = P(B/A) x P(A) / P(B)

 

P(B)를 모를 때, P(A|B) = P(B|A)P(A) / P(B|A)P(A) + P(B|A')P(A')

ex) 김씨는 유방조영술을 이용해서 유방암을 검진하려고 한다. 40-50대 여성이 유방암에 걸릴 확률은 0.8%이다. 유방암에 걸렸을 때, 유방조영술을 통해서 양성(Positive)로 나올 확률은 90%이다. 유방암이 아니더라도 유방조영술이 양성일 확률은 7%이다. 김씨는 유방조영술을 통해 양성이라고 검진되었고, A의사는 여성이 유방암에 걸렸을 확률이 90%라고 하고, B의사는 10%라고 하고, C의사는 50%라고 한다. 김씨는 어떻게 판단해야 할까?

여성이 유방암에 걸릴 확률(A) : P(A) = 0.008

유방암일 때(A) 유방조영술이 양성인 경우(B) : P(B|A) = P(A∩B) / P(A) = 0.9

유방암이 아닐 때(A') 유방조영술이 양성인 경우(B) :

  >> P(B|A') = P(A' ∩ B) = P(A') = 0.07

유방조영술이 양성(B)일 때, 유방암(A)일 확률 :

  >>  P(A|B) = P(A ∩ B) / P(B) = P(B|A)P(A) / P(B) = (0.9)(0.0008) / P(B)