Deep Learning [Day 1]

고려대학교 김중헌 교수님

Curriculum

• Basics
• Software Installation and Examples
• Linear Regression
• Binary Classification
• Softmax Classification
• Artificial Neural Networks(ANN)
• Convolutional Neural Networks(CNN)
• CNN for CIFAR-10
• Recurrent Neural Networks(RNN)
• Generative Adversarial Networks(GAN)

1. Basics

1.1. Machine Learning Overview

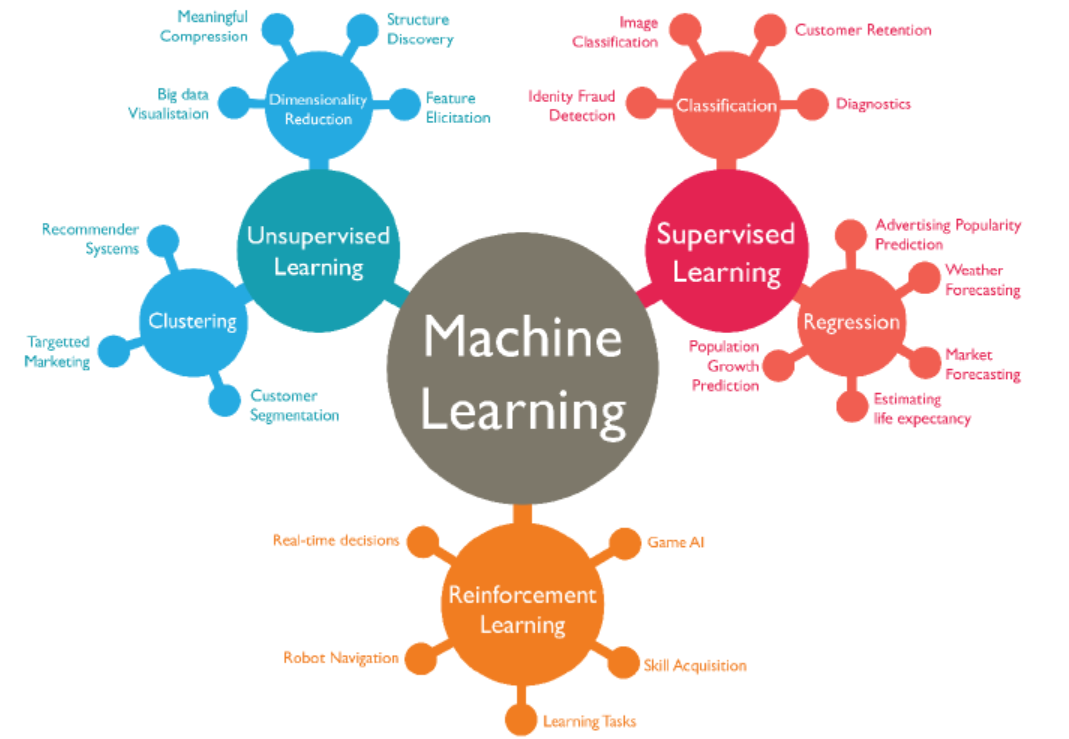
• AI는 전 분야에 미칠 수 있는 기술이기에, 계속해서 열광할 것.
• 머신러닝은 크게 비지도 학습과 지도학습, 그리고 강화학습으로 나눌 수 있다.
• 강화학습은 지도학습/비지도학습의 단일 응답 구조와 다르게 끊임없이 응답하는 구조(바둑과 같은 게임에 있는 AI 알고리즘은 한 수를 두고 끝나는 것이 아니라 상대방의 수를 읽고서, 다음 수를 생각하면서 진행한다.)
  
  

1.2. Introduction

딥러닝 프로세스 과정

1) 모델 만들기(껍데기) - MLP(Multi-Layer Perception), CNN, RNN, GAN, Customized

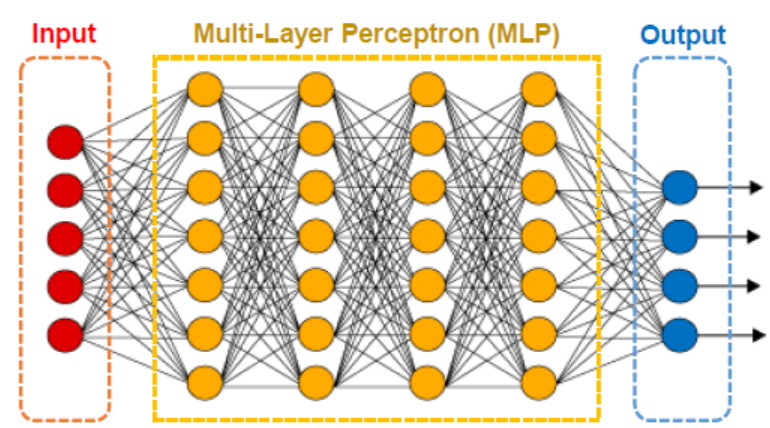
input(5개의 유닛) -> 4개의 히든레이어 + 7개의 유닛 -> output(4개의 유닛)

2) 훈련하기 - 입력된 데이터를 레이블링할 수 있도록

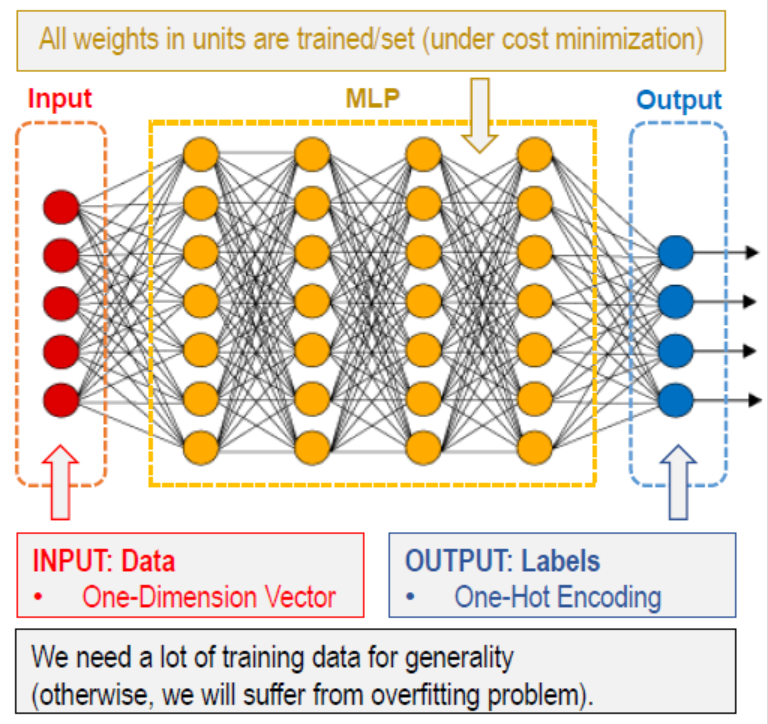
3) 테스팅/추론 - 현실의 row 데이터를 테스팅하여 결과물이 유의미하도록

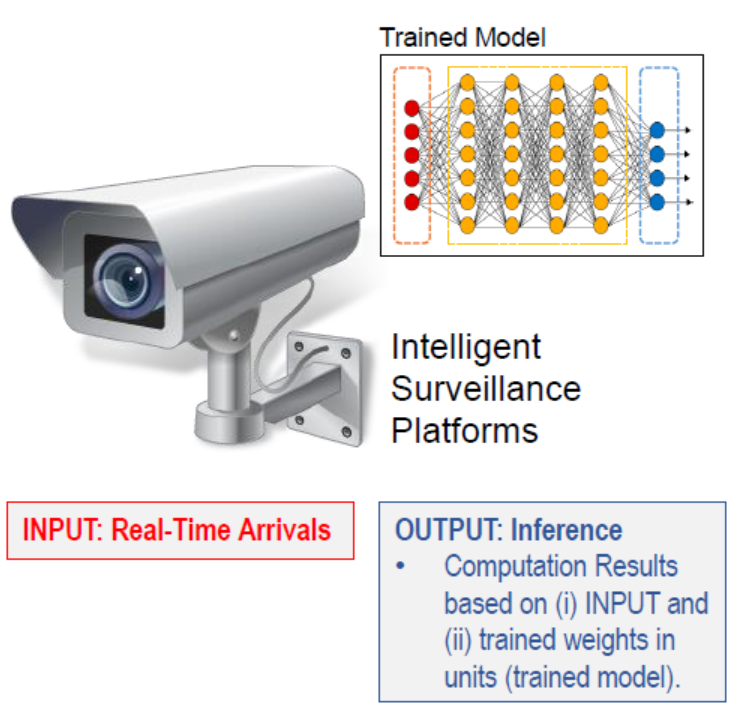
※ 딥러닝 과정에서 발생되는 문제

Overfitting

• 2단계에서 발생되는 문제로, 데이터가 충분하지 않은 경우 발생한다.
• 훈련 결과는 엄청 높게 나왔는데, 테스트 결과는 엄청 낮은 것을 과적합 문제라 한다.
• 예를 들어, 침대를 팔고 싶어서 데이터를 수집하고자 하는데, 나의 잠자리 유형에만 특화된 침대만을 학습시키면 훈련은 잘 나올지 몰라도, 다른 사람들의 잠자리 유형에 맞지 않는 침대가 나올 수 있다.
• 더 많은 훈련 데이터가 필요하다!

딥러닝에서 두 가지 주요 모델(CNN, RNN)

CNN(Convolutional Neural Network)

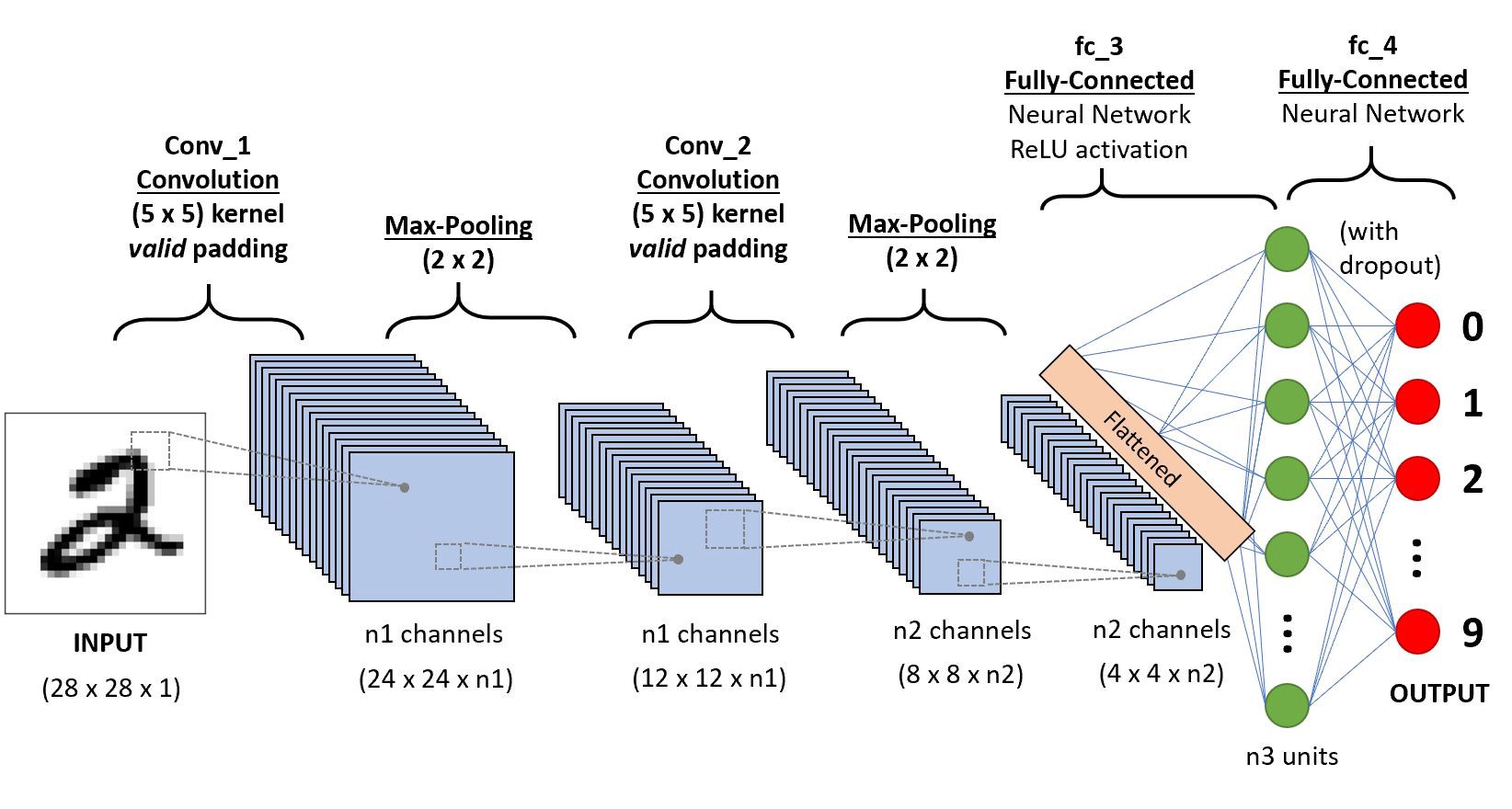
• 기존의 딥러닝은 1차원 구조만 입력이 가능하지만 많은 응용 분야에서 입력은 다차원이 필요했다. CNN은 2차원 구조(이미지), 3차원 구조(영상)을 훈련시킬 수 있다.
• 주로 시각 정보 학습에 사용한다.

RNN(Recurrent Neural Network)

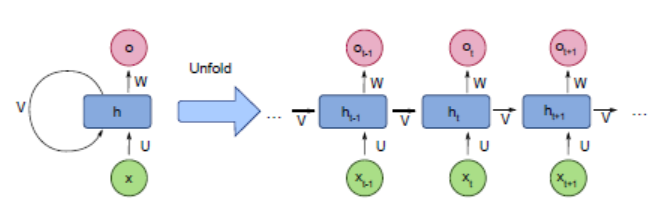
• 기존의 신경망 아키텍처에는 시간의 개념을 사용할 방법이 없었다. 이러한 시계열 데이터를 학습시킬 수 있는 모델이 주로 LSTM 및 GRU이다.
• 주로 시계열 정보 학습에 사용한다.
  
  

2. Linear Regression

2.1. Linear Regression Theory

• regression은 예측하는 것을 목표로 한다.
• linear model은 흔히 직선 방정식을 생각하면 된다. 이 linear model은 통계학에서는 가설(hypothesis)이라고 부른다.

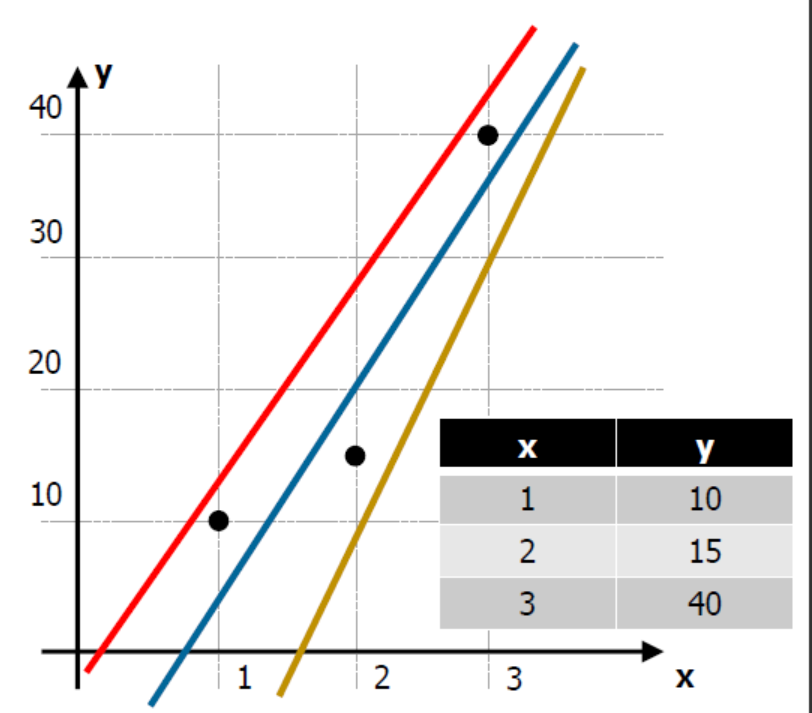
• 위의 사진과 같이 3개의 직선 중 어느 직선이 가장 좋아보일까? 아마도, 예측 측면이나 분류 측면 모두 가운데 파란색 선이 가장 좋아보인다고 할 수 있을 것이다.
• 따라서 우리는 파란색 선과 같이 점과 직선 사이의 거리가 최소한이 되는 새로운 직선을 계속해서 만들어내야 한다.

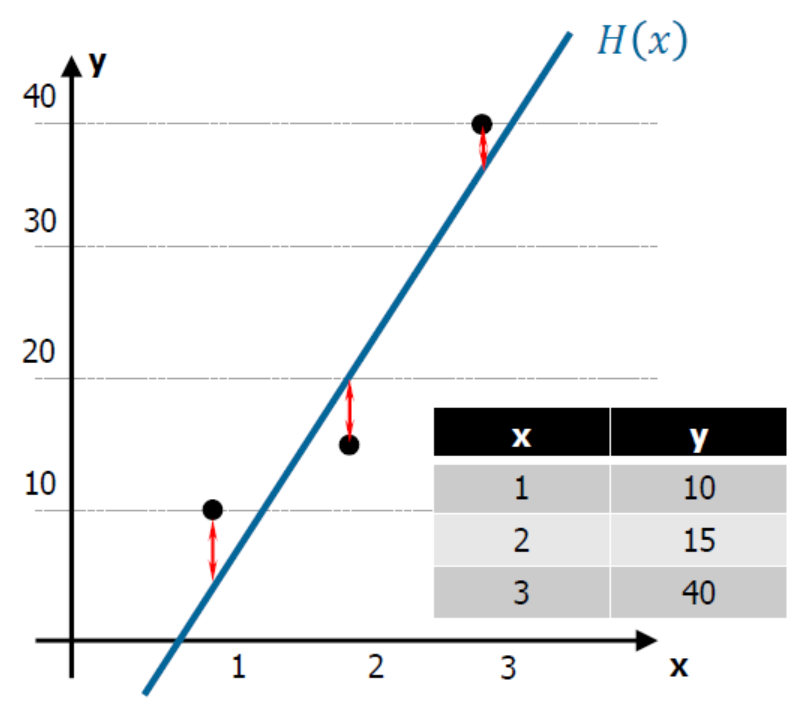
• 위의 사진과 같이 점과 직선 사이의 거리는 오차(cost, 비용)라고 할 수 있으며, 비용 또는 손실함수로 만들 수 있다.

• 이러한 비용함수는 실제값과 예측값의 차이를 제곱(음수가 될 수 있기 때문에, 어차피 우리는 그 차이만을 보는 것이기 때문에 제곱을 해도 상관없다.)하여 평균을 내주면 만들 수 있다.
• 따라서 비용함수는 2차 방정식 형태의 곡선이 만들어진다.

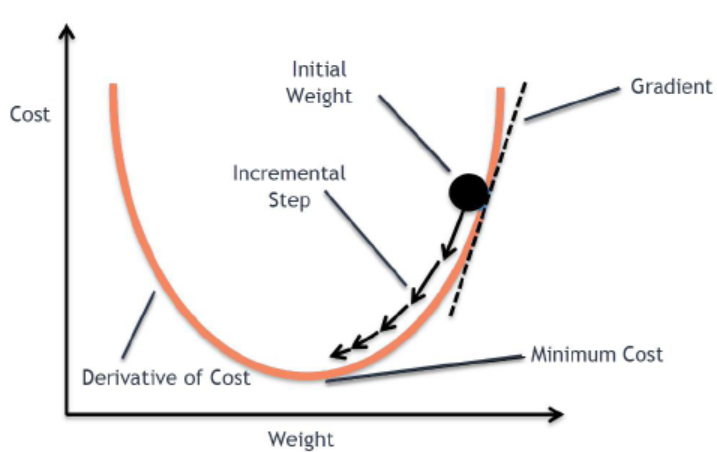
• 고등수학을 배웠다면 쉽게 이해할 수 있겠지만, 2차 방정식을 미분하게 되면 1차 방정식의 직선이 된다. 이 직선은 gradient(기울기)라고 하며, 오차값이 된다. 따라서 우리는 오차를 최대한 줄이기 위해서 기울기가 0이 되도록 만들어야 하는데, 위의 사진과 같이 점점 기울기의 크기가 작아지도록 만드는 것을 Gradient Descent Method(경사하강법) 라고 한다.

• 경사하강법 과정 중에서 기울기가 작아지도록 만들 때, 필요한 것이 learning rate이다. 한 번 학습할 때 얼마만큼 학습해야 하는지의 학습 양을 의미하며, learning rate를 적절하게 조정해줘야 모델의 학습이 잘 될 수 있다.
• learning rate가 크다는 것은 경사하강을 할 때 step이 크다는 것이다. step이 크면 왔다갔다 하거나, 위로 튕겨 올라가버릴 수 있다. 이는 학습이 이루어지지 않으며, 쓰레기값이 나올 수 있다. 또한, 이러한 현상을 overshooting이라고 한다.
• learning rate가 작다는 것은 경사하강을 할 때 step이 작다는 것이다. step이 작으면 너무 천천히 내려가기 때문에 시간이 다해 최저점이 아님에도 불구하고 멈추어 버린다.

• 이러한 현상들을 피하기 위해서는 cost함수를 출력해보고 작은값으로 변화하고 있다면 learning rate를 증가시켜보면서 관측해야 한다.

  Multi-Variable Linear Regression

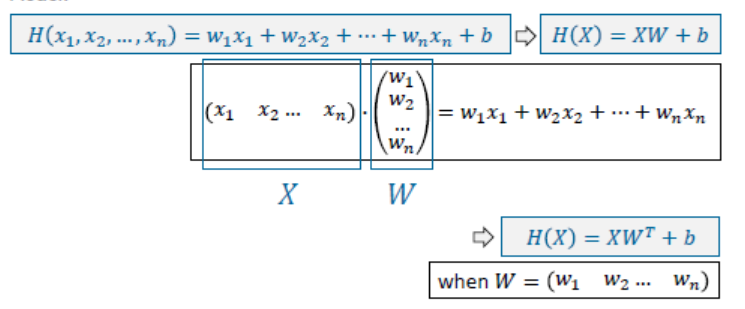
• 다중 변수로 linear model을 만들기 위한 방정식과 비용함수를 만들 수 있는데, 방정식에서 더욱 깔끔하게 나타낼 수 있도록 선형대수인 행렬을 사용한다.
  
  

2.2. Linear Regression Implementation

Tensorflow

(1, 1)일 때는 10, (2, 2)일 때는 20, (3, 3)일 때는 30, (4, 4)일 때는?

import tensorflow as tf

x_data = [[1, 1], [2, 2], [3, 3]]
y_data = [[10], [20], [30]]

# placeholder: 공간확보(예약)
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

# y = Wx + b
W = tf.Variable(tf.random_normal([2, 1])) # 가중치. Variable: 변수 생성, random_normal: [2, 1] 모양의 정규분포를 가지는 난수 생성
b = tf.Variable(tf.random_normal([1])) # 기준

model = tf.matmul(X, W) + b # Wx + b라는 행렬식
cost = tf.reduce_mean(tf.square(model - Y)) # 오차(최소제곱법)
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # 비용함수를 줄이기 위한 경사하강법

# tensorflow는 session을 항상 만들어줘야 한다.
with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())

  # Training
  for step in range(2001):
    c, W_, b_, _ = sess.run([cost, W, b, train], feed_dict={X: x_data, Y: y_data}) # train 결과값은 빈 값이므로, _ 형태로 변수를 만들어준다.
    print(step, c, W_, b_)

  # Testing
  # (4, 4)일 때를 알고 싶으니까
  print(sess.run(model, feed_dict={X: [[4, 4]]}))

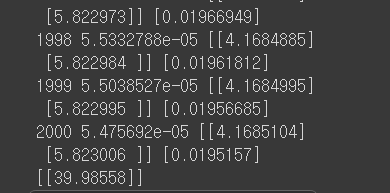
Keras

1일 때는 1, 2일 때는 2, 3일 때는 3, 4일 때는?

import numpy as np
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense

x_data = np.array([[1], [2], [3]])
y_data = np.array([[1], [2], [3]])

# Model, Cost, Train
model = Sequential()
# 첫 번째 인자: 레이어 수(여기서는 output layer 1개)
# input_dim: 입력되는 차원 수. [[1]] -> 1차원, [[1, 2]] -> 2차원
# activation: 활성함수
# 1) linear: 디폴트값, 입력 뉴런과 가중치로 계산된 결과값이 그대로 출력됨
# 2) relu: 이미지에서 주로 사용
# 3) sigmoid: binary classification에서 주로 사용
# 4) softmax: softmax classification에서 주로 사용
model.add(Dense(1, input_dim=1, activation=None))
model.compile(loss='mse', optimizer='adam')
model.fit(x_data, y_data, epochs=1000, verbose=1)
model.summary()

print(model.get_weights())
print(model.predict(np.array([[4]])))

plt.scatter(x_data, y_data)
plt.plot(x_data, y_data)
plt.grid(True)
plt.show()

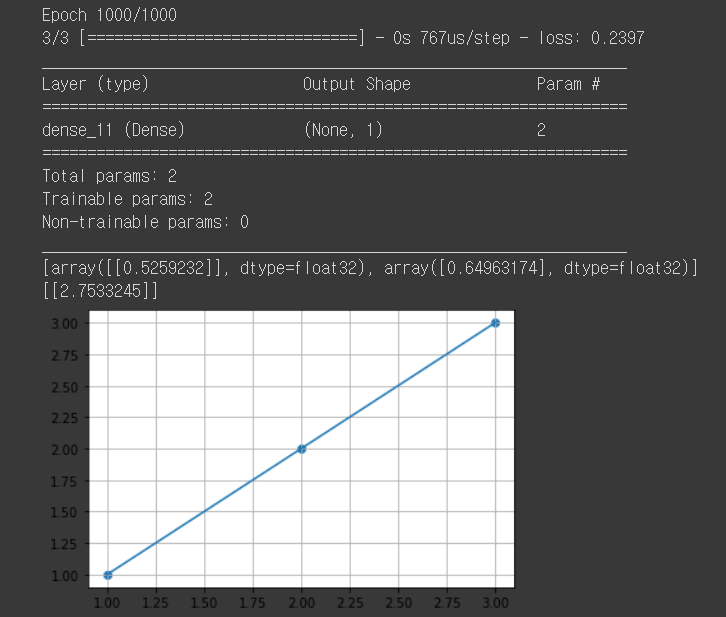
3. Binary Classification

3.1. Binary Classification Theory

• classification은 분류하는 것을 목표로 한다.
• Binary classification은 0 또는 1로만 나누어지는 것으로, 스팸 메일인지(1) 아닌지(0)와 같은 예시를 들 수 있다.
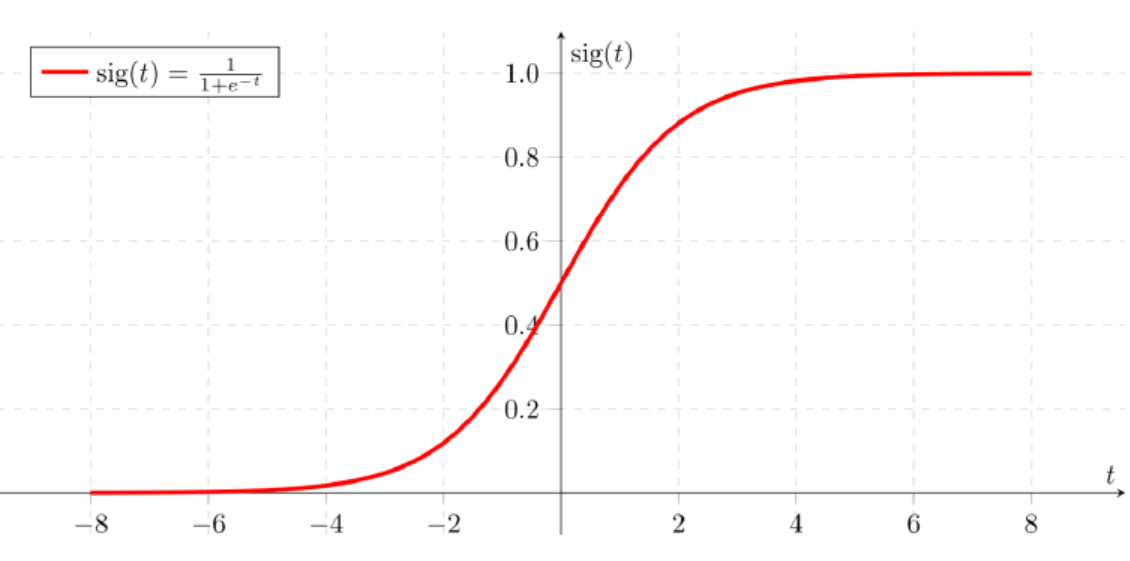
• Binary classification은 기본적으로 Linear regression의 H(x) = Wx + b와 같은 1차 방정식을 따르면서, 0과 1의 분류를 하는 기준이 있다. 이러한 기준을 bias라고 하며, 이는 문제에 따라 바뀌기 때문에 Logistic/sigmoid function을 사용한다.

• 그렇다면, 왜 시그모이드 함수를 사용하는지를 알아보자. 0 또는 1과 같이 데이터를 분류하기 위해선 단순 직선의 방정식은 사용하기가 어렵다. 왜냐하면, 현재 데이터의 분포에 따라 직선으로 나누었다고 하더라도, 새로운 데이터의 값이 어디에 위치하는지에 따라 또 다시 새로운 모델이 필요하기 때문이다. 따라서 계속해서 모델의 변화를 만들어주는 것이 아닌, 시그모이드 함수를 만들어서 0과 1로 분류하게 한다.

• 변수가 1개인 선형 방정식은 목표가 실수값 예측이기 때문에 선형함수 y = Wx + b를 이용하여 예측한다(예측 변수의 수가 하나인 경우). 하지만 binary classification에서는 목표값이 0 또는 1이기 때문에 y = Wx + b를 이용해서 분류하는 것은 의미가 없다고 앞서 언급했다. 그래서 확률(Probability)을 이용하는데 다음과 같이 정의 된다.

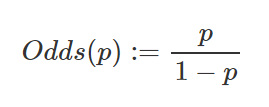
• 확률 p의 범위가 (0, 1)이라면, Odds(p)의 범위는 (0, \(\infty\))가 된다. 이를 로그함수를 취하면 범위가 (\(-\infty\), \(\infty\))가 된다. 즉, 범위가 실수 전체가 되어 분석을 하는 것이 의미가 있다.

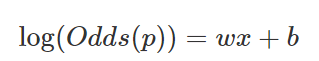
• 다시 위의 식을 p로 정리하면 다음과 같은 함수를 얻을 수 있고, 이 함수을 시그모이드라 한다.

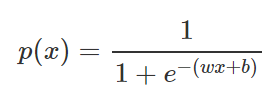
• 따라서 binaray classification의 logistic model은 다음과 같다.

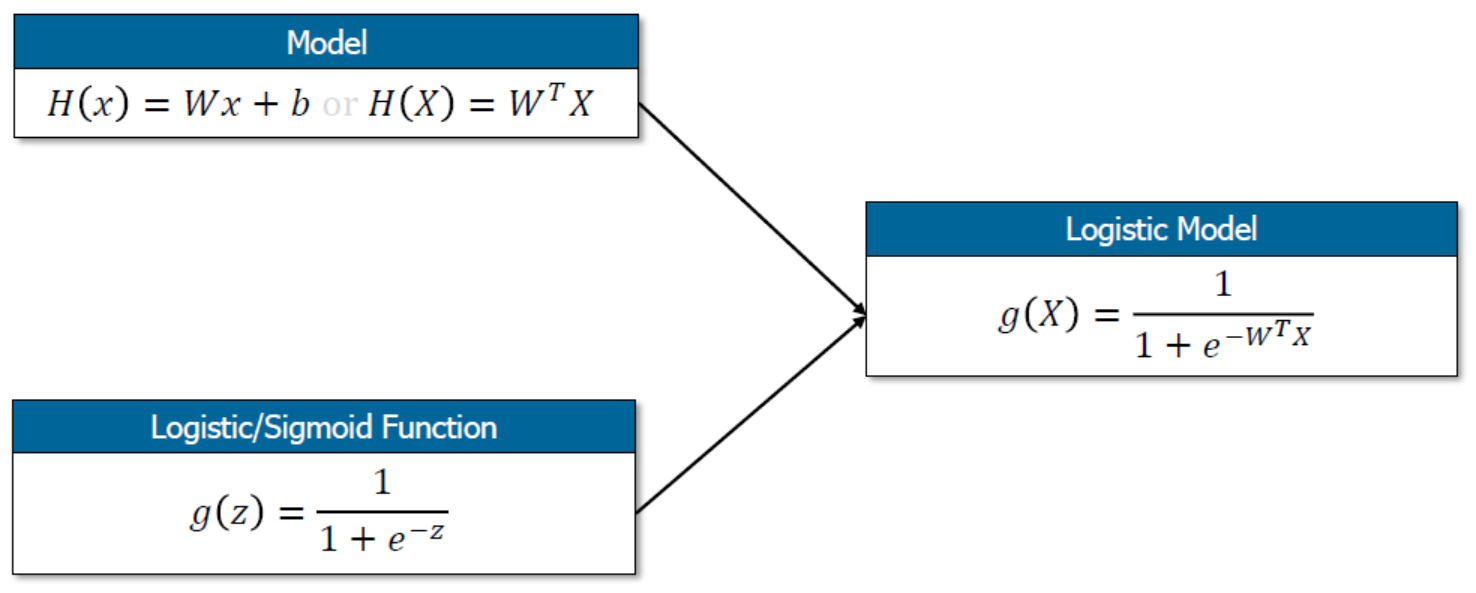
• 기존의 linear regression model에서 새로운 모델로 바뀌었으니, 당연히 그에 따른 비용함수도 새롭게 맞춰줘야 한다. 시그모이드 함수는 linear 모델과 다르게 비용함수를 구하기 위해 제곱해서 평균을 해도 분모가 더욱 커지게 되어 곡선이 나올수가 없다. 따라서 다음과 같은 비용함수를 만들어준다.

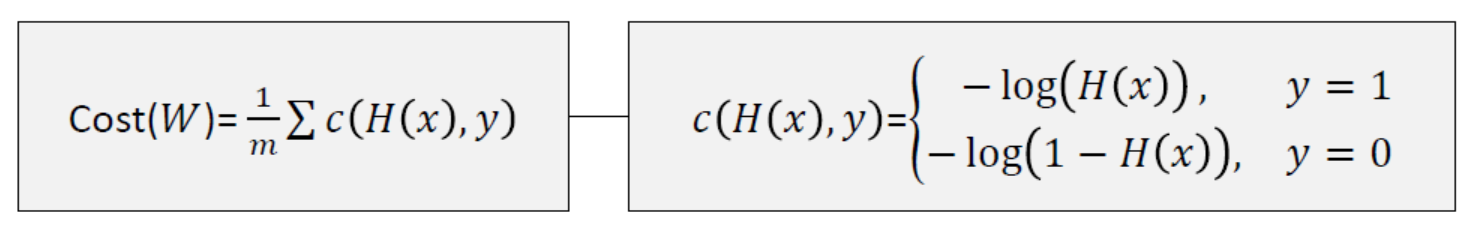
• H(x)는 일차 방정식이고 y는 목표값으로, y와 H(x)의 값에 따라 비용이 달라진다. 아래의 그림과 같이 y와 H(x)의 값이 같을 경우에(실제값과 예측값이 정확할 때)만 cost가 0이 되고, 다를 경우에는 무한대 값이 나온다.

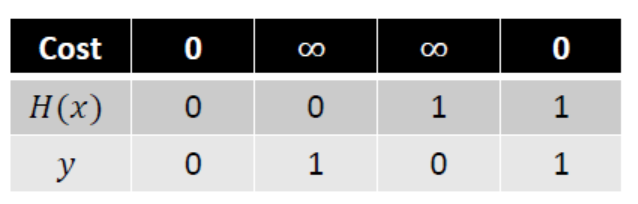
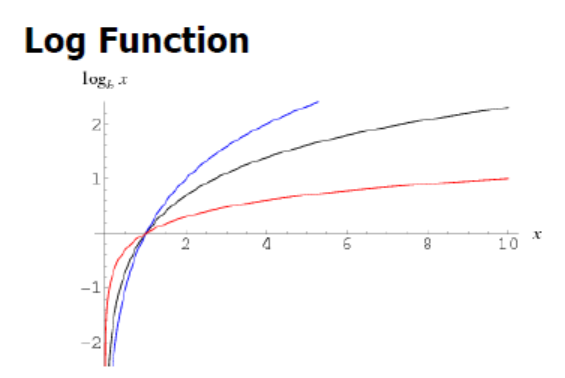
• 이와 같은 로그 기반으로 이루어진 함수를 엔트로피 함수라고 한다. 추가적으로 설명하자면, 엔트로피는 불확실성을 나타내며, 어떤 데이터가 나올지 예측하기가 어렵다는 것이다. 즉, 엔트로피가 높다는 것은 정보가 너무 많아서 계산해야 할 확률이 더 많아지기 때문에 예측이 더욱 어려워진다는 것이다.

• 예시로, 동전 던지기와 주사위 던지기가 있다고 하자. 동전 던지기에서 앞/뒷면이 나올 확률은 각각 1/2이지만, 주사위 던지기에서는 각각의 숫자가 나올 확률이 1/6이다(이론적인 확률). 이를 위와 같이 로그함수를 만들어주면, 동전의 엔트로피 값은 약 0.693, 주사위의 엔트로피 값은 약 1.79로 주사위의 엔트로피 값이 더 높다.

• 이러한 엔트로피 함수를 적용한 비용함수를 좀 더 간결하게 한 줄로 표현하기 위해서 다음과 같이 쓸 수 있다.

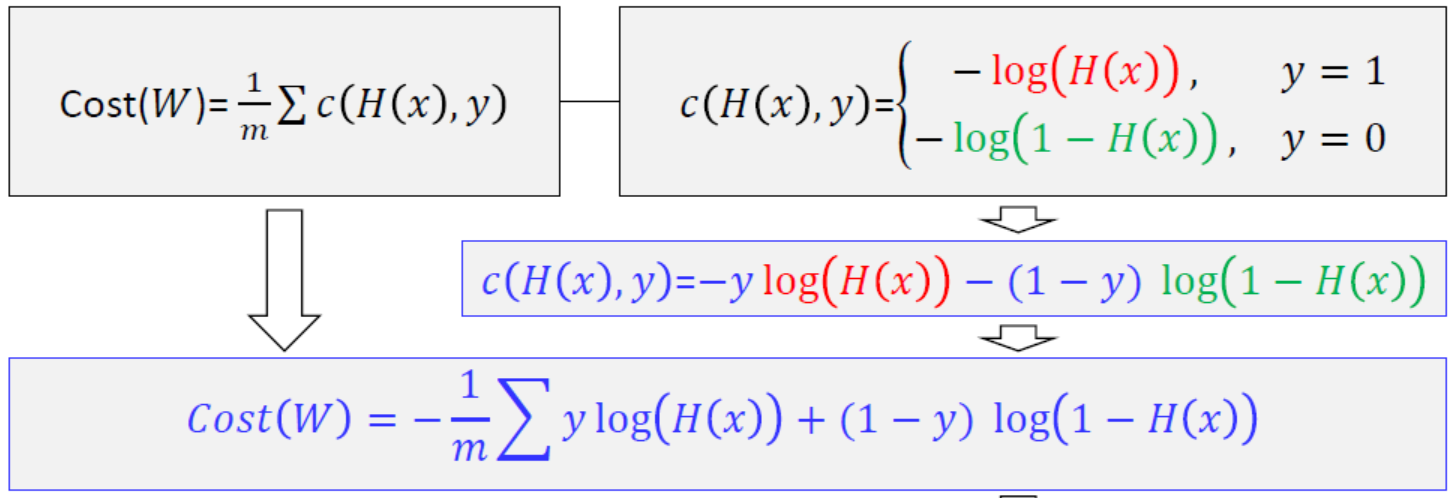
3.2. Binary Classification Implementation

Tensorflow

(1, 2), (2, 3), (3, 1)은 0, (4, 3), (5, 3), (6, 2)는 1로 나뉘었을 때, 모델의 정확도는?

import numpy as np
import tensorflow as tf

x_data = np.array([[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]])
y_data = np.array([[0], [0], [0], [1], [1], [1]])

X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([2, 1]))
b = tf.Variable(tf.random_normal([1]))

# Model, Cost, Train
model = tf.sigmoid(tf.add(tf.matmul(X, W), b))
cost = tf.reduce_mean((-1) * Y * tf.log(model) + (-1) * (1-Y) * tf.log(1-model))
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

prediction = tf.cast(model > 0.5, dtype=tf.float32) # model의 값이 0.5보다 크면 참값이 되어 1을, 작으면 거짓값이 되어 0을 반환
accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, Y), dtype=tf.float32))

with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())

  # Training
  for step in range(10001):
    cost_val, train_val = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
    print(step, cost_val)

  # Testing
  h, c, a = sess.run([model, prediction, accuracy], feed_dict={X: x_data, Y: y_data})
  print("\nModel: ", h, "\nCorrect: ", c, "\nAccuracy: ", a)

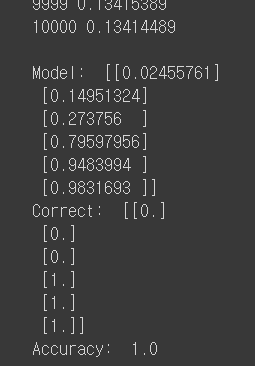
당뇨병 환자들의 csv 파일을 읽고 분류해보자.

import numpy as np
import tensorflow as tf

xy = np.loadtxt('data-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1] # 마지막 열 제외하고 나머지 열의 모든 행 가져오기
y_data = xy[:, [-1]] # 마지막 열의 모든 행 가져오기

X = tf.placeholder(dtype=tf.float32, shape=[None, x_data.shape[1]])
Y = tf.placeholder(dtype=tf.float32, shape=[None, 1])

W = tf.Variable(tf.random_normal([x_data.shape[1], 1]))
b = tf.Variable(tf.random_normal([1]))

# Model, Cost, Train
model = tf.sigmoid(tf.add(tf.matmul(X, W), b))
cost = tf.reduce_mean((-1) * Y * tf.log(model) + (-1) * (1-Y) * tf.log(1-model))
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

prediction = tf.cast(model > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, Y), dtype=tf.float32))

with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())

  # Training
  for step in range(100001):
    c, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
    print(step, c)

  # Testing
  h, c, a = sess.run([model, prediction, accuracy], feed_dict={X: x_data, Y: y_data})
  print("\nHypothesis: ", h, "\nCorrect (Y): ", c, "\nAccuracy: ", a)

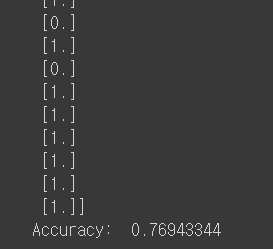
Keras

(1, 2), (2, 3), (3, 1)은 0, (4, 3), (5, 3), (6, 2)는 1로 나뉘었을 때, 모델의 정확도는?

import numpy as np
from keras.models import Sequential
from keras.layers import Dense

x_data = np.array([[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]])
y_data = np.array([[0], [0], [0], [1], [1], [1]])

# Model, Cost, Train
model = Sequential()
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['accuracy'])
model.fit(x_data, y_data, epochs=10000, verbose=1)
model.summary()

print(model.get_weights())
print(model.predict(x_data))

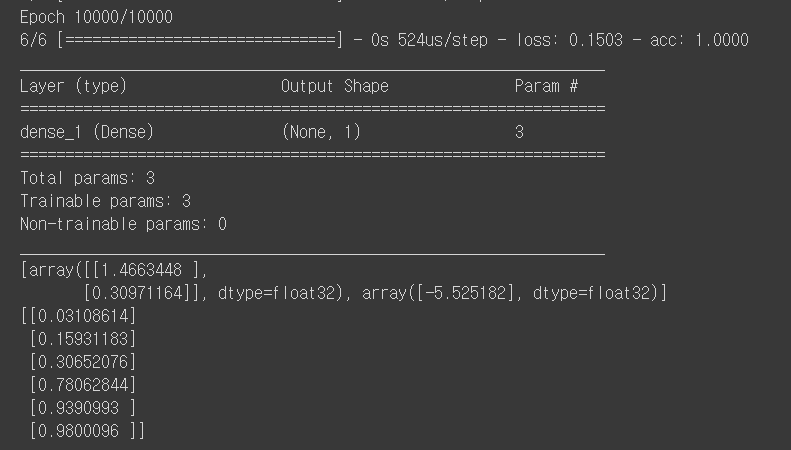
x_data의 분류를 해봤을 때, 앞에 3개는 0.5보다 작고, 뒤에 3개는 0.5보다 큰 것을 확인할 수 있다.

당뇨병 환자들의 csv 파일을 읽고 분류해보자.

import numpy as np
from keras.models import Sequential
from keras.layers import Dense

xy = np.loadtxt('data-diabetes.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]

# Model, Cost, Train
model = Sequential()
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['accuracy'])
model.fit(x_data, y_data, epochs=1000, verbose=1)
model.summary()

print(model.get_weights())
print(model.predict(x_data))

4. Softmax Classification

4.1. Softmax Classification Theory

• binary classification이 0과 1로만 분류를 했다면, softmax classification은 0, 1, 2, 3 등과 같이 다중값을 분류한다(Multinomial Classification이라고도 한다).

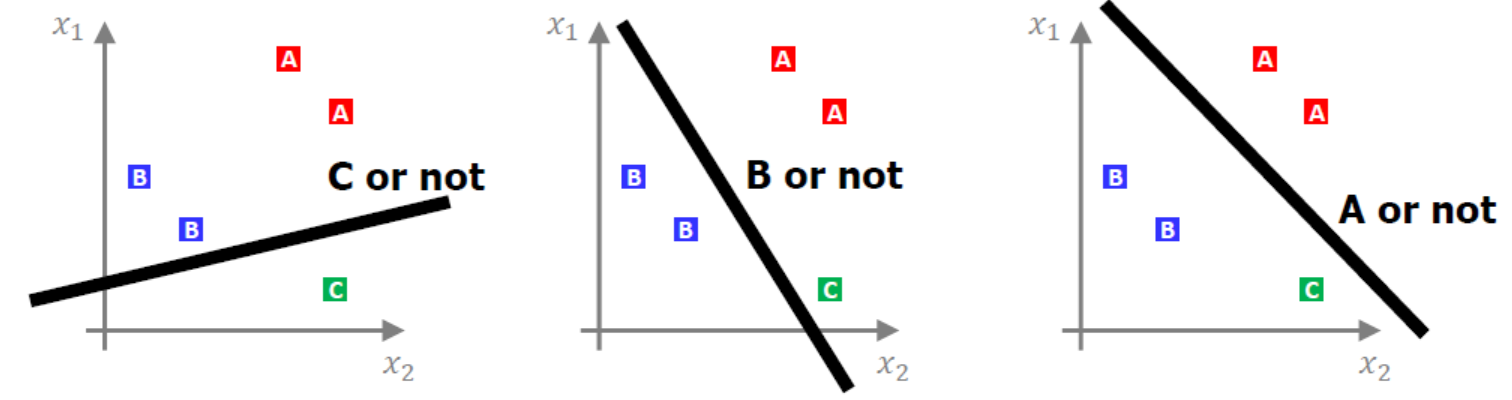
• 그렇다면 어떤 기준으로 다중 분류를 할 수 있을까? 답은 binary classification을 베이스로 하되, 질문을 여러 번하면 된다. 즉, 아래의 그림에서는 다음과 같이 여러 번 질문을 하며 모델이 학습할 수 있도록 한다.

A인가 아닌가
B인가 아닌가
C인가 아닌가

• 따라서 binary classification과 같이 H(x)를 만들기 위해선, 질문을 3번하게 되면 식이 3개가 나와야 하기 때문에 번거롭다. 이를 하나의 식으로 표현해주기 위해서 선형대수의 행렬을 사용한다.

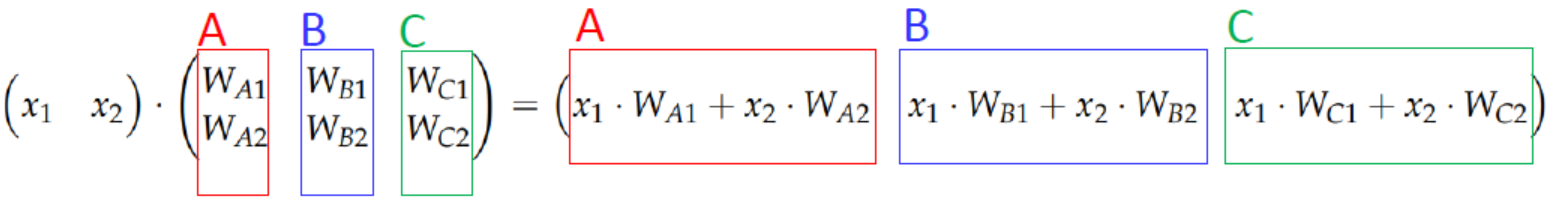
• 비용함수의 경우도 각 질문마다의 확률이 나오기 때문에, 이를 One-Hot Encoding 형태로 바꿔준다. 즉, \(A=0.7, B=0.56, C=0.09\)면, 시그모이드 값이 높은 것으로 결정하여, \(A=1, B=0, C=0\)으로 바꿔준다. 이러한 과정이 바로 Softmax 함수라고 한다.

• 다시 정리하자면, binary classification에서 사용한 시그모이드 함수는 입력된 데이터에 대해서 0과 1사이의 값을 출력하여, 해당 값이 둘 중 하나에 속할 확률로 해석할 수 있도록 만들어준다. 예를 들어 0이 정상 메일, 1이 스팸 메일이라고 정의해놓는다면 시그모이드 함수의 0과 1사이의 출력값을 스팸 메일일 확률로 해석할 수 있다. 확률값이 0.5(기준)를 넘으면 1에 더 가까우므로 스팸 메일로 판단하고, 그 반대면 정상 메일로 판단한다.

• 이번에는 softmax classification과 같이 2개 이상의 답을 고른다. 앞에서 나온 시그모이드 함수를 사용한다면, 첫 번째가 정답일 확률은 0.7, 두 번째가 정답일 확률은 0.6, 세 번째가 정답일 확률은 0.4 등과 같은 출력을 얻게된다. 그런데 이 전체 확률의 합계가 1이 되도록 하여 전체 정답지에 걸친 확률로 바꿀 순 없을까? 만약 하나의 샘플 데이터에 대한 예측값으로 모든 가능한 정답지에 대한 정답일 확률의 합이 1이 되도록 구할 수 있다면 3가지 선택지 중 가장 높은 확률을 고르면 될 것이다. 이러한 것이 가능하도록 하는 함수가 Softmax 함수이다.

• Softmax Classification에서 주로 사용하는 비용함수는 Cross-Entropy 함수이다.

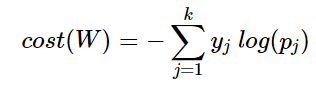
• 위의 그림에서 y는 실제값을 나타내며, k는 클래스의 개수로 정의한다. \(y_j\)는 실제값 One-Hot vector의 j번째 인덱스를 의미하며, \(p_j\)는 샘플 데이터가 j번째 클래스일 확률을 나타낸다. 표기에 따라서 \(\widehat y_j\)로 표현하기도 한다.

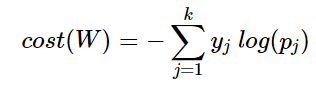
• c를 실제값 One-Hot vector에서 1을 가진 원소의 인덱스라고 한다면, \(p_c = 1\)은 \(\widehat y\)이 y를 정확하게 예측한 경우가 된다. 이를 식에 대입해보면 \(−1log(1) = 0\)이 되기 때문에, 결과적으로 \(\widehat y\)가 y를 정확하게 예측한 경우의 크로스 엔트로피 함수의 값은 0이 되며, 최소화하는 방향으로 학습해야 한다.

• 이제 이를 n개의 전체 데이터에 대한 평균을 구한다고 하면, 최종 비용 함수는 다음과 같다.

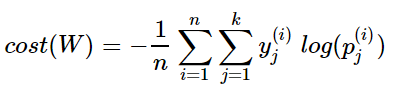
• 위의 함수를 좀 더 직관적으로 살펴보면, S를 추정치(예측값)로 하고, L을 실제값으로 하여 다음과 같이 볼 수 있다.

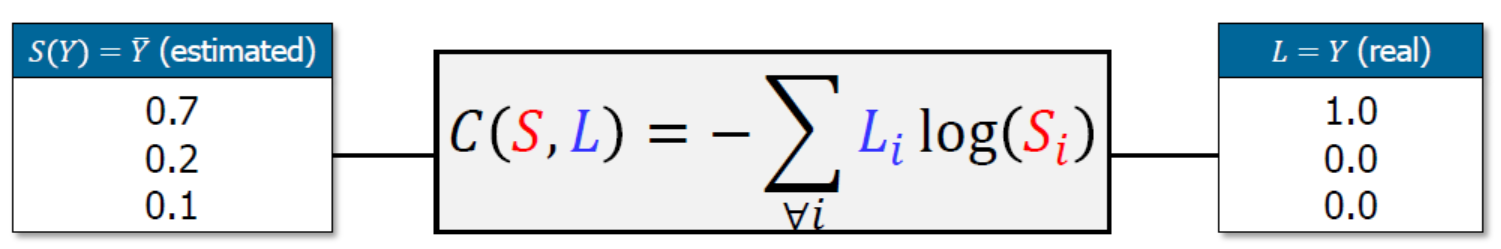
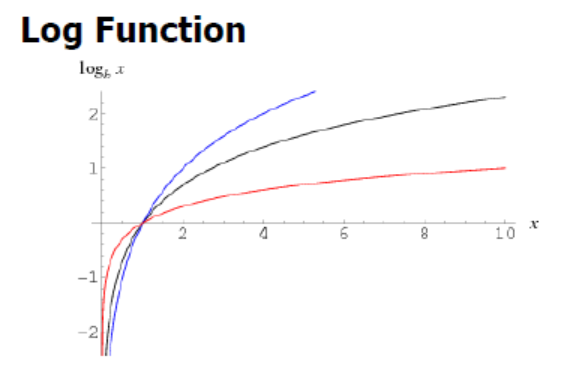
• 크로스엔트로피 함수는 실제값과 예측값이 맞는 경우에는 0으로 수렴하고, 값이 틀릴경우에는 값이 커지기 때문에(\(\infty\)), 실제 값과 예측 값의 차이를 줄이기 위한 엔트로피라고 할 수 있다.
  
  

• 결국, 위에서 보았던 binary classification에서 사용된 엔트로피 함수 역시 크로스엔트로피 함수라고 할 수도 있으며, 본질적으로 softmax classification의 크로스엔트로피 함수와 동일한 수식이다.

  증명

  • binary classification에서 사용된 크로스엔트로피 함수식은 다음과 같다.

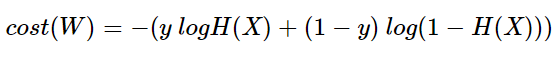
• 위의 식에서 \(y 를 y_1, y-1 를 y_2\)로 치환하고, \(H(x)를 p_1, 1-H(X)를 p_2\)로 치환하면 다음과 같다.

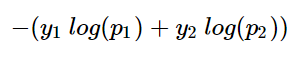
• 위 식은 다시 다음과 같이 만들 수 있으며, 이는 softmax 함수에서 \(k=2\)를 넣은 동일한 함수이다.

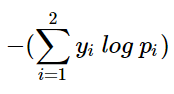
4.2. Softmax Classification Implementation

Tensorflow

입력되는 벡터값에 대해서 [0, 0, 1], [0, 1, 0], [1, 0, 0]의 3가지로 분류하기.

import tensorflow as tf

x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5], [1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]

X = tf.placeholder(tf.float32, shape=[None, 4]) # shape의 행이 None인 이유는 train 데이터와 test 데이터의 행의 개수가 다르기 때문에. 열은 같으므로 4로 고정
Y = tf.placeholder(tf.float32, shape=[None, 3])

# W: 4x3, b: 3 -> 총 15개의 변수를 학습
W = tf.Variable(tf.random_normal([4, 3]))
b = tf.Variable(tf.random_normal([3]))

# model을 softmax하기 전으로 나눈 이유는 cost 함수를 구하는 함수에서 이미 softmax가 포함되어 있기 때문에
model_LC = tf.add(tf.matmul(X, W), b)
model = tf.nn.softmax(model_LC)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=model_LC, labels=Y))
train = tf.train.GradientDescentOptimizer(0.1).minimize(cost)

with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())

  # Training
  for step in range(2001):
    c, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
    print(sess, c)

  # Testing
  test1 = sess.run(model, feed_dict={X: [[1, 11, 7, 9]]})
  print(test1, sess.run(tf.argmax(test1, 1))) # test1 모델의 열을 기준으로 가장 큰 값의 좌표값(2차원 배열이기 때문에 1을 사용할 수 있음)

Keras

* Keras Tip
1. Linear Regression - loss: mse
2. Binary Classification - activation: sigmoid, loss: binary_crossentropy
3. Softmax Classification - activation: softmax, loss: categorical_crossentropy

import numpy as np
from keras.models import Sequential
from keras.layers import Dense

x_data = np.array([[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5], [1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]])
y_data = np.array([[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]])

# Model, Cost, Train
model = Sequential()
model.add(Dense(3, activation='softmax')) # 3개의 유닛([0, 0, 1], [0, 1, 0], [1, 0, 0])을 가진 출력층
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
model.fit(x_data, y_data, epochs=10000, verbose=1)
model.summary()

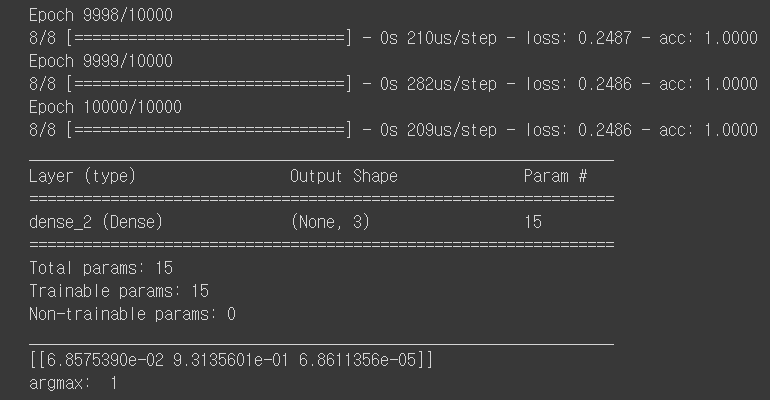
y_predict = model.predict(np.array([[1, 11, 7, 9]]))
print(y_predict)
print("argmax: ", np.argmax(y_predict))

※ 정리

linear regression

일차식(Wx + b)이 기본 모델이며, 입력값에 대한 추정치에 따른 오차를 구하기 위해 최소자승법(제곱하여 평균)을 이용하고, 구해진 오차를 경사하강법을 통해 줄여나간다.

binary classification

일차식(Wx + b)에서 단순히 직선그래프가 아니라, 기준이 바뀔 수 있다는 점을 감안하여, 시그모이드 함수로 모델을 만든다. 오차를 구하기 위해 엔트로피 함수를 만들고, 구해진 오차를 경사하강법을 통해 줄여나간다.

softmax classification

binary classification과 다르게 2개 이상의 값을 분류해야 한다. 소프트맥스 함수로 모델을 만들고, 오차를 구하기 위해 크로스 엔트로피 함수를 만들고, 구해진 오차를 경사하강법을 통해 줄여나간다.