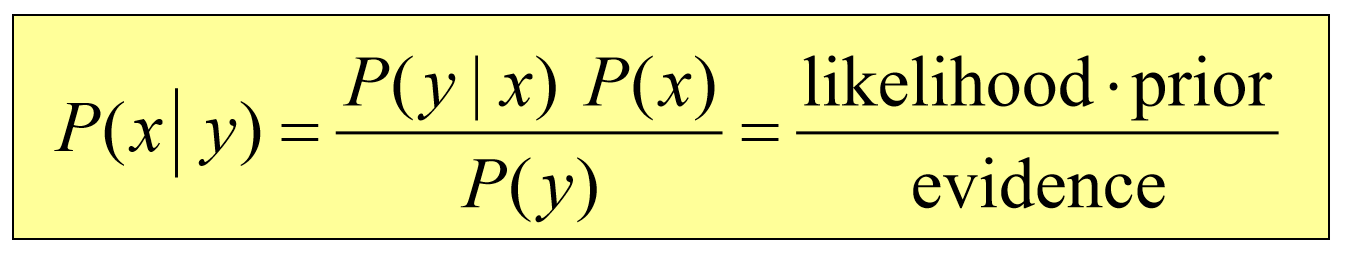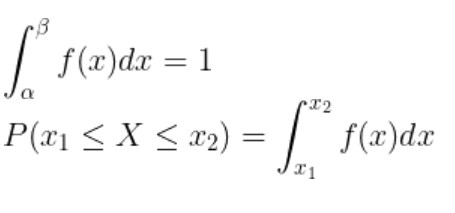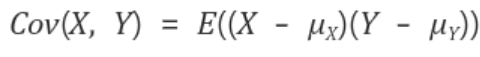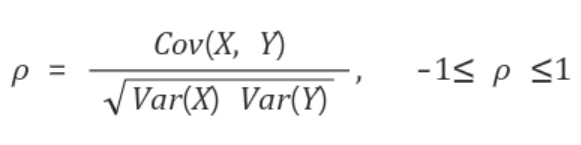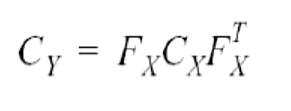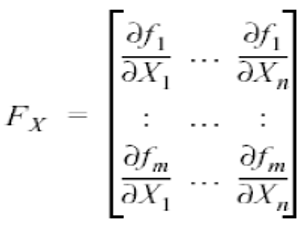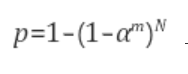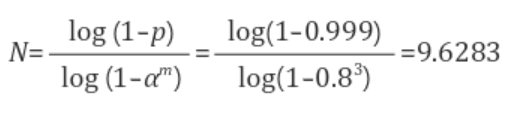Perception with Uncertainty
Contents
- From object recognition to scene/place recognition
- Probabilistic Primer
- Uncertainties
- Representation + Propagation
- Line extraction from a point cloud
- Split-and-merge
- Line-Regression
- RANSAC
- Hough Transform
1. From object recognition to scene/place recognition
- 모바일 로봇이 가지는 scene/place 인지
- loop closure 문제와 kidnapped robot 문제
- loop closure은 이전의 위치로 돌아갈 수 있는지이고, kidnapped robot은 로봇을 어느 곳에 놓던지간에 자신의 위치를 파악하여 목적지까지 잘 도달할 수 있는지이다.
- BoW(Back of Words)
- 이미지 분류에서 단어(word)에 해당하는 것은 지역 이미지 특성들(local image features)이다.
- 특성들은 SIFT나 SURF와 같은 영상 특징점(keypoint) 추출 알고리즘에 의해 결정되기도 하고, 간단한 이미지 지역 패치로 결정되기도 한다.
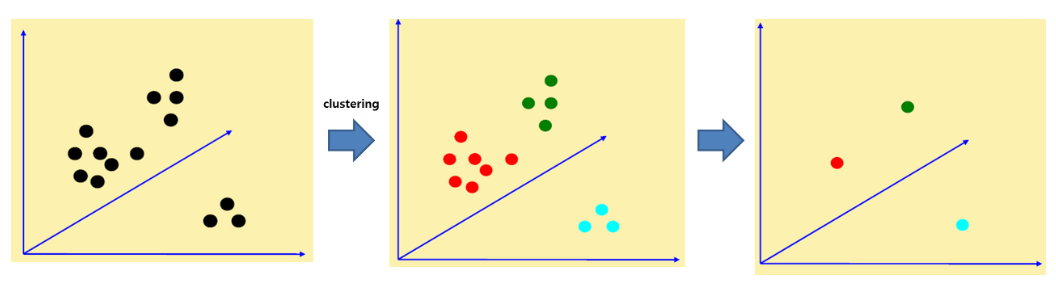
- 여러 장의 이미지로부터 도출된 특성들 중에는 유사한 것들이 존재할 것이다. 따라서 특성들 중에서 비슷한 것들을 하나로 모아주기 위해 k-means와 같은 군집(clustering) 방법을 사용한다.
- 군집의 센터점들에 코드워드(codeword)를 부여해주고, 코드워드들로 구성된 코드북(codebook)이 만들어진다. 코드북은 visual vocabulary로 불러진다.
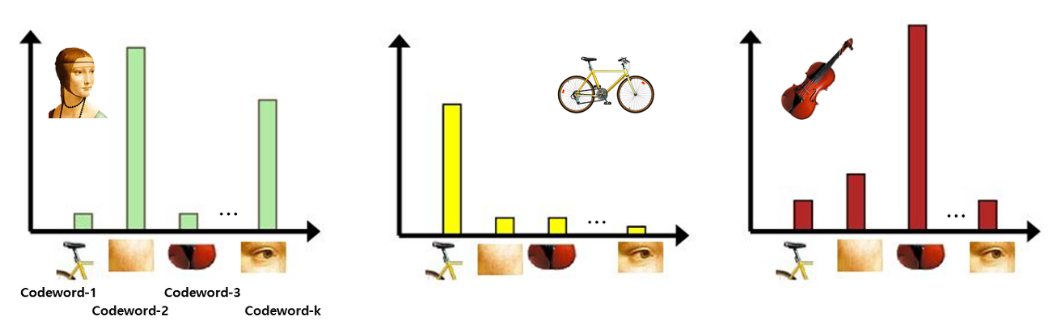
- 코드북이 완성되면 각 이미지를 코드북을 이용해서 표현할 수 있다. 이미지에서 도출된 특성들과 코드북의 코드워드들 중에서 가장 비슷한 것을 찾는다. 한 이미지 특성이 코드워드1과 가장 유사하면 코드워드1 빈(bin)을 하나 채워준다.
- 이러한 방식으로 이미지 내의 특성들을 코드워드들과 매칭해주면 히스토그램이 만들어진다. 히스토그램을 보면 각 이미지마다 어떤 코드워드들이 많이 포함되어 있는지를 알 수 있다.
2. Probabilistic Primer
- Conditional Probability(조건부 확률)
-
p(x y) = p(X=x Y=y) - 조건부 확률에서 각각의 사건은 독립적이다.
-
- Discrete Random Variables(이산 확률 변수)
- 확률변수란 어떤 시행의 결과에 따라 변수 X가 취할 수 있는 값과 그 확률이 각각 정해질 때, 이 변수 X를 확률변수(random variable)이라고 한다.
- 이산확률변수는 확률변수 X가 취할 수 있는 값이 유한하기 때문에 셀 수 있는 확률변수이다.
- Continuous Random Variables (연속 확률 변수)
- 연속확률변수는 확률변수 X가 취할 수 있는 값이 어떤 범위에 속하는 모든 실수로 무한하기 때문에 셀 수 없는 확률변수이다.
- Bayes Formula(베이즈 정리)
- 사전확률(prior probability)를 설정, 사건 발생 -> 사후확률(posterior possibility) 계산 가능
- 모바일 로봇에서의 베이즈 정리
- p(x): 로봇의 추정위치
- p(y): 센서값이 읽히는 시점
3. Uncertainties
- 현실 세계의 센서는 항상 불확실하다(노이즈가 있다).
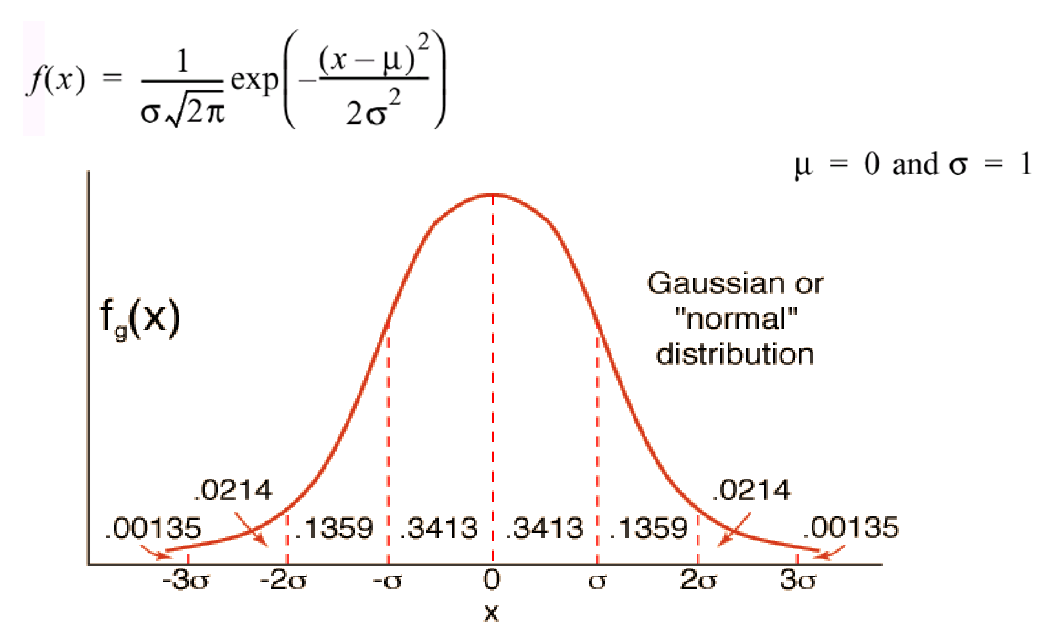
- Probability Density Function(PDF)
- 확률질량함수(Probability Mass Function, PMF)는 이산확률변수의 확률분포를 나타내는 함수이다. 즉, 확률변수가 취할 수 있는 값이 유한개이거나 자연수와 같이 셀 수 있는 이산확률변수일 때, 그 불연속한 값에 대한 확률을 나타내는 함수이다.
- 연속확률변수의 경우 확률변수가 취할 수 있는 값이 연속적이며 무한하기 때문에 분포를 표현하는 것이 불가능하다. 만약 이산형처럼 특정한 확률변수 하나에 특정한 확률값에 대응된다면, 어떤 확률변수가 특정한 구간 안에 포함될 확률은 무한대가 된다.
- 그렇다고 특정한 확률변수의 값에 대한 확률값을 0으로 설정할 수도 없다. 이렇게 되면 특정 구간 안에 확률변수가 포함될 확률은 어느 구간에서든 0이 되어버리기 때문이다.
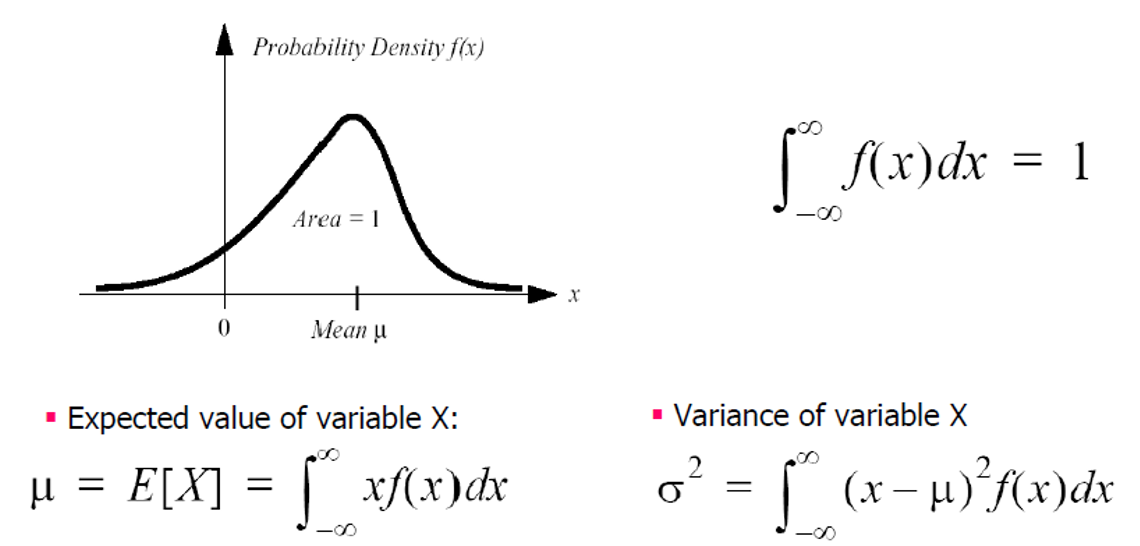
- 이러한 난점을 돌파하기 위해 확률밀도함수(Probability Density Function, PDF)가 필요하게 되었다.
- 확률밀도함수가 정의된 구간 내에 연속확률변수 X가 포함될 확률은 1이며, 특정 구간 \(x_1과 x_2\)에 연속확률변수 X가 포함될 확률은 확률밀도함수를 그 구간에 대해 정적분한 것과 같다.
- 확률밀도함수를 가우시안 분포를 이용해 표현할 수도 있다.
- Uncertainty Propagation
- 불확실성의 전파는 변수의 불확실성에 기반한 함수의 불확실성에 미치는 영향이다.
- 불확실성 u는 절대오차, 상대오차 등으로 정의될 수 있으며, 가장 일반적으로 분산의 양의 제곱인 표준편차 \(\sigma\)로 정량화된다.
- 불확실성의 값과 오차는 구간 (x+u, x-u)로 표시된다. 또한, 변수의 통계적 확률 분포가 알려져 있거나 추정될 수 있는 경우 변수의 참값이 발견될 수 있는 영역을 설명하는 신뢰구간을 도출할 수 있다.
- 분산이 클수록 각각의 값들이 평균값에서 멀리 떨어져있다는 것이며, 이는 곧 표준편차 역시 커지므로, 불확실성이 높다고 할 수 있다.
- 불확실성이 상관관계(correlation)에 있는 경우에는 공분산(Covariance)를 고려해야 한다.
- 공분산은 확률변수 X의 편차(평균으로부터 얼마나 떨어져있는지)와 확률변수 Y의 편차를 곱한 것의 평균값이다.
- 공분산이 0보다 크면 X가 증가할 때 Y도 증가한다는 뜻이며, 공분산이 0보다 작으면 X가 증가할 때 Y는 감소한다.
- 공분산이 0이면 두 변수간에는 아무런 상관관계가 없다.
- 즉, 공분산은 두 변수간에 양의 상관관계가 있는지, 음의 상관관계가 있는지 정도를 알려준다. 하지만 상관관계가 얼마나 큰지는 제대로 반영하지 못한다.
- 공분산의 문제는 확률변수의 단위 크기에 영향을 많이 받는다는 것이다. 이를 보완할 수 있는 것이 상관계수이다.
- 상관계수는 확률변수의 절대적 크기에 영향을 받지 않도록 공분산을 단위화시킨 것이다. 즉, 공분산에 각 확률변수의 분산을 나누어준다.
- 상관계수는 양의 상관관계가 있는지, 음의 상관관계가 있는지 알려줄 뿐만 아니라, 그 상관성이 얼마나 큰지도 알려준다.
- 1 또는 -1에 가까울수록 상관성이 큰 것이고, 0에 가까울수록 상관성이 작은 것이다.
- 공분산 행렬 \(C_y\)는 에러 전파 법칙에 의해 다음 식으로 표현될 수 있다.
- \(C_x\): 입력 불확실성을 표현하는 공분산 행렬
- \(C_y\): 출력을 위해 전파된 불확실성을 표현하는 공분산 행렬
- \(F_x\): Jacobin 행렬
- Jacobin Matrix
- 로봇의 움직임을 고려하면 가장 중요한 주제가 기준좌표(reference frame) 변환이다. 사람은 (x, y, z)로 이루어진 직교좌표계(cartesian coordinate)로 바라보기를 원하지만, 로봇은 극좌표계(polar coordinate)로 명령을 내려주길 바란다.
- 이러한 인간과 로봇의 좌표계를 이어주는 역할을 하는 것이 바로, 자코비안이다.
- Joint space(로봇의 움직임)을 Task space(3차원 공간의 움직임)으로의 변환을 만들어주고자 필요하다.
- Jacobian은 복잡하게 얽혀있는 식을 미분을 통해 linear approximation시킴으로써 간단한 근사 선형식으로 만들어준다.
- 간단히 말해서, 다변수 함수일 때의 미분값이다.
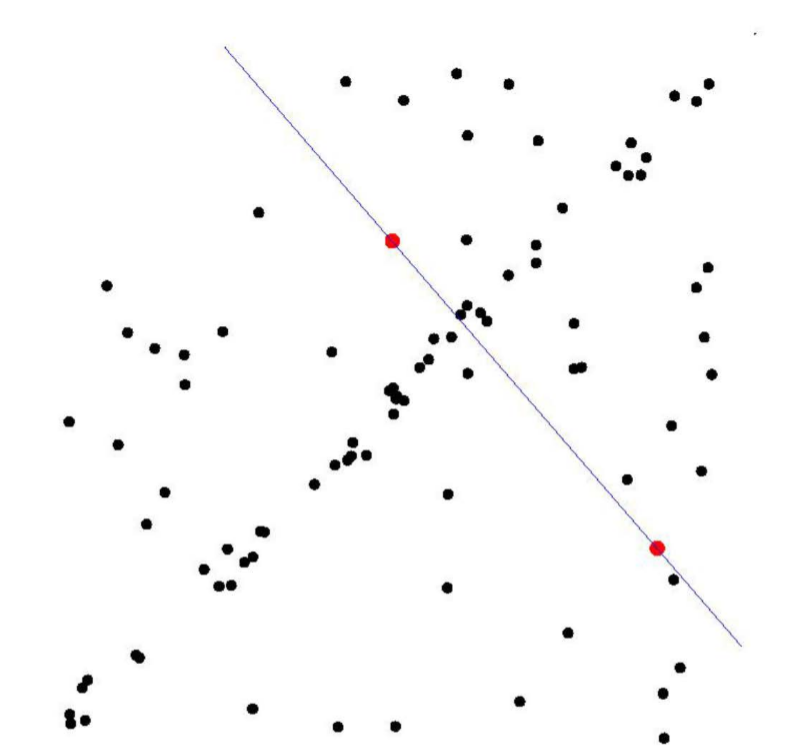
- Line Extraction from a point cloud
- point cloud로부터 라인을 어떻게 찾을 것인가?
-
3가지의 의문점이 있다.
1) 얼마나 많은 선들이 있는지?
2) 어떤 점들이 어떤 선에 포함되어 있는지?
3) 선 위에 점이 주어졌을 때, 어떻게 선의 파라미터들을 계산할 수 있는지? -
다음 알고리즘들은 위의 의문점을 해결해 줄 것이다.
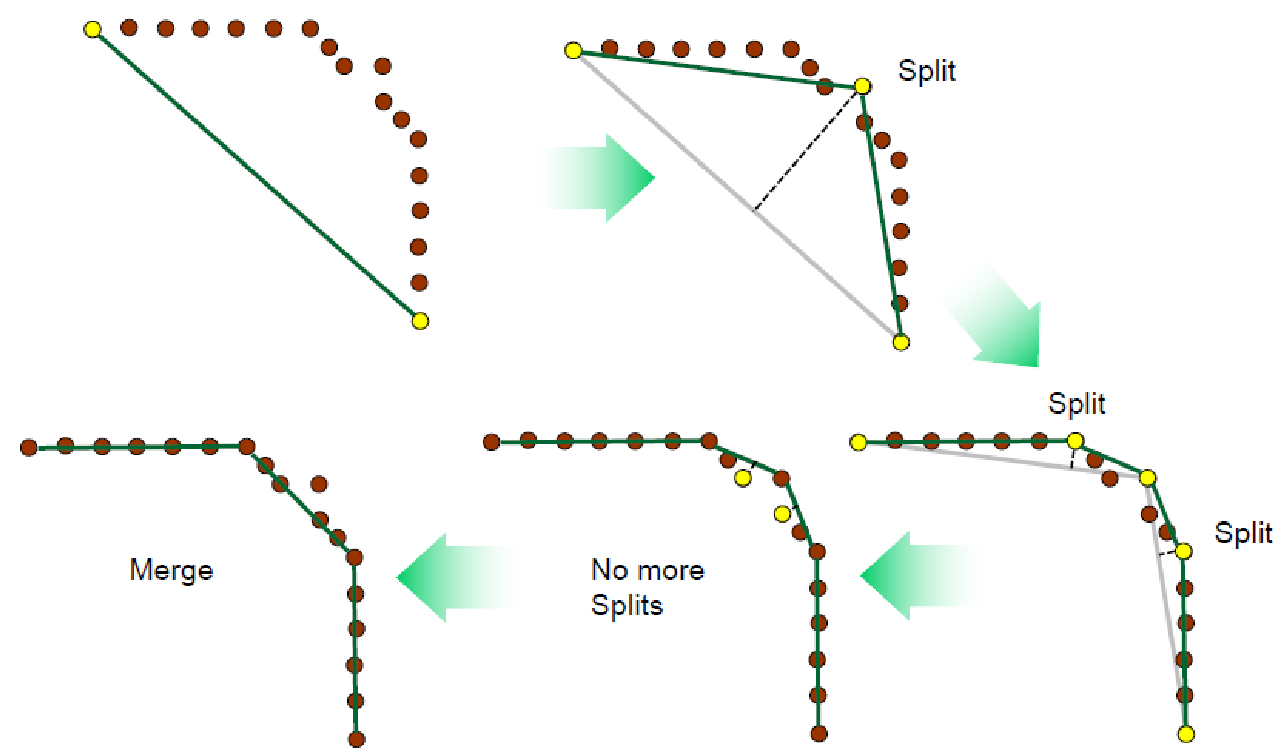
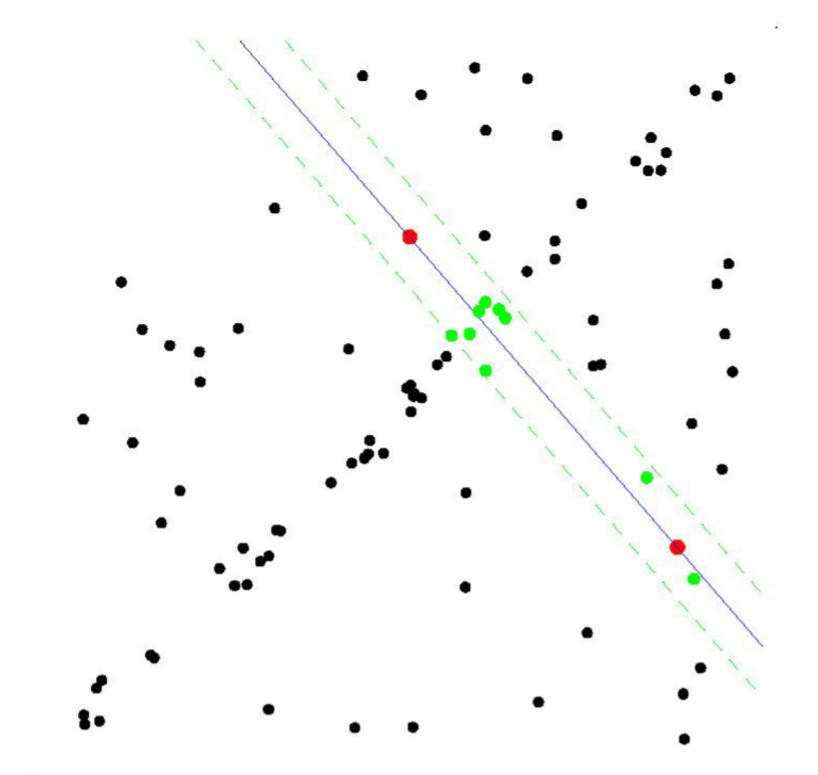
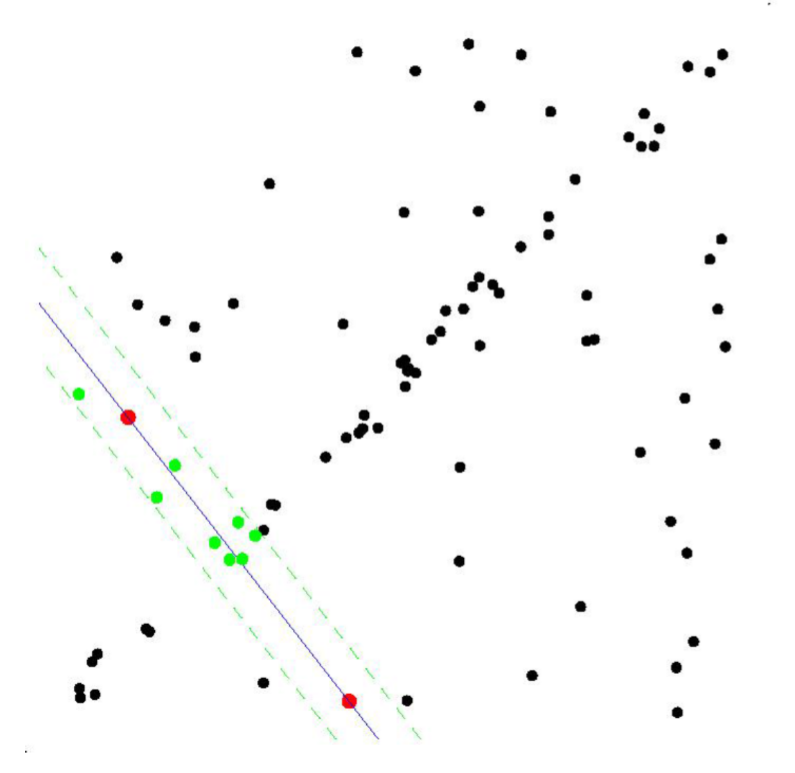
1) split-and-merge 방법
- 라인을 유지하는 포인트를 찾아서 그룹핑
- 포인트셋이 주어지면 split(가장 멀리 떨어진 포인트를 찾기, 그 라인을 기준으로 split)
- merge(연속된 두 세그먼트들을 그룹핑) -> split(threshold보다 크다 아니다를 따지기) -> merge 계속 반복
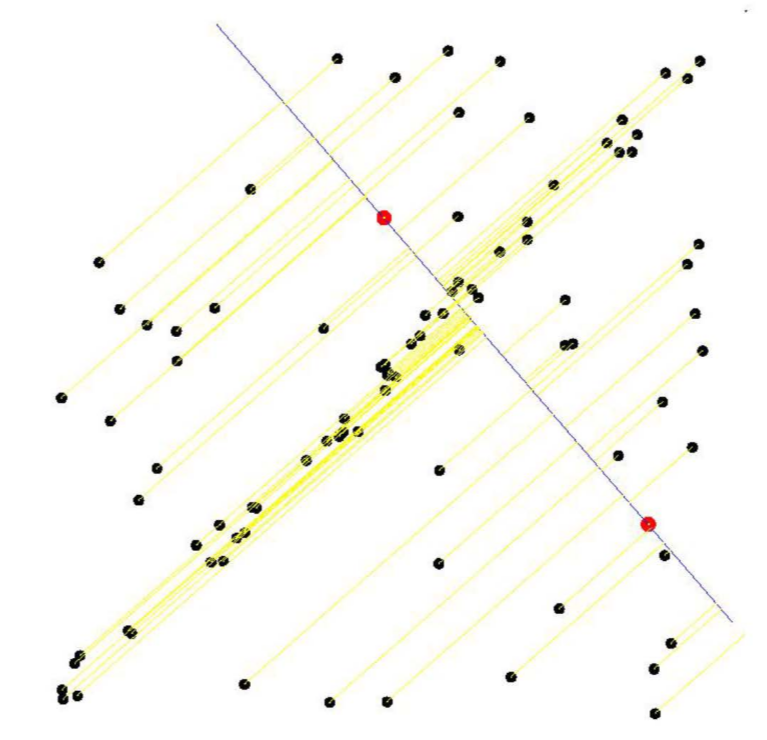
2) linear regression
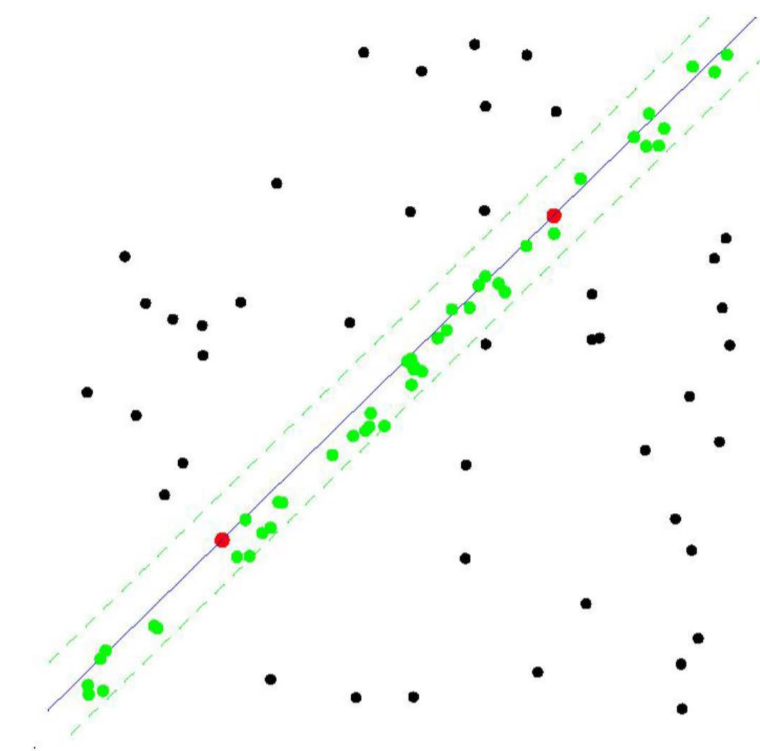
3) RANSAC(RANdom SAmple Consensus)
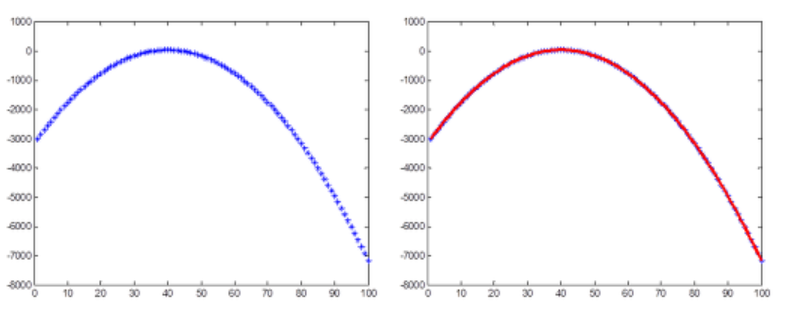
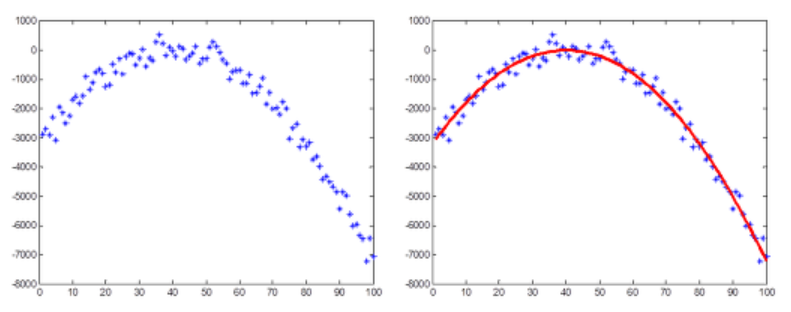
- RANSAC이 필요한 이유는 다음 그림들을 통해 알 수 있다. 첫 번째 그림에서 관측된 데이터들을 최소자승법을 이용하여 포물선으로 근사시킨 그림이다.
- 하지만 실제 관측 데이터는 노이즈(noise)로 인해서 두 번째 그림과 같은 경우가 일반적일 것이다. 이때도 최소자승법을 적용하여 포물선으로 근사시켜 이쁘게 나타낼 수 있다.
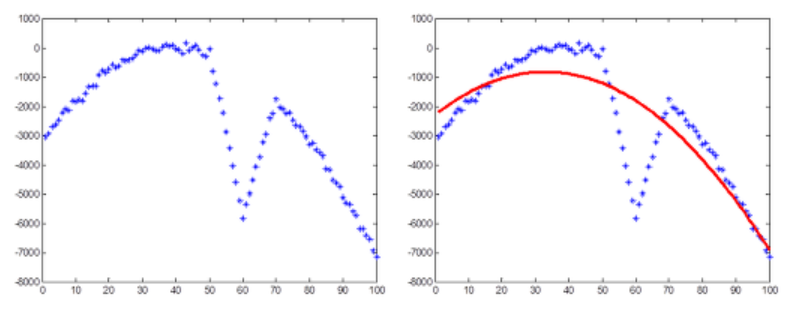
- 그렇지만, 만약 세 번째 그림과 같이 이상점(outlier)가 있는 데이터의 경우 최소자승법을 이용해도 이상한 포물선을 그릴 것이다.
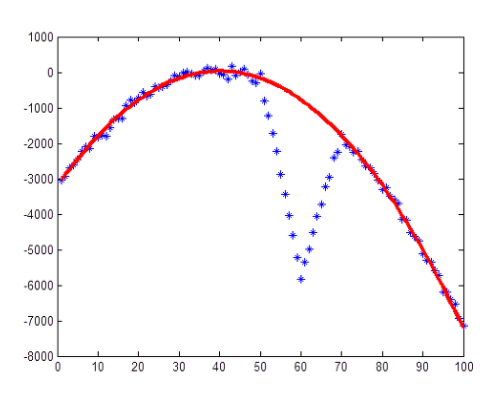
- 하지만 이를 RANSAC을 이용해 근사시키면 마지막 그림과 같이 깨끗한 결과를 얻을 수 있다.
- 최소자승법은 데이터들과의 잔차를 최소화하도록 모델을 찾지만, RANSAC은 가장 많은 수의 데이터들로부터 일치하는 모델을 선택하는 방법이다.
- 결국, 최소자승법과 RANSAC은 무엇을 기준으로 파라미터를 찾는가의 차이이다. 따라서, RANSAC의 기준을 사용하면 관측 데이터에 outlier가 많더라도 데이터 근사가 가능하다는 것이다.
- RANSAC 알고리즘
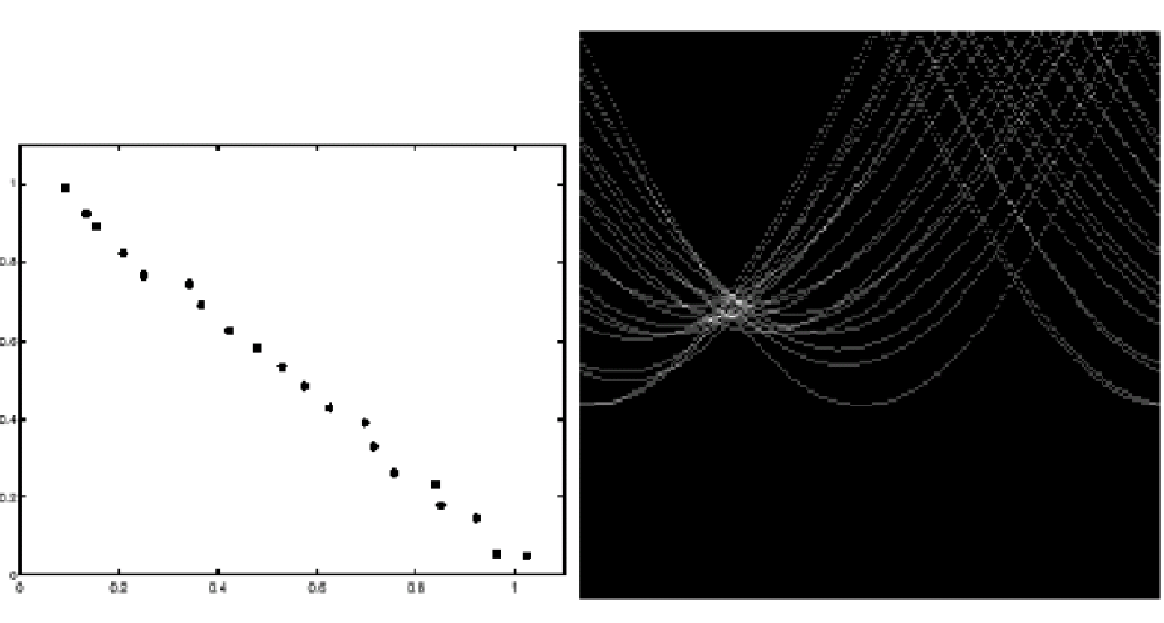
a) 샘플링 과정을 몇 번(N) 반복할 것인지
-> RANSAC을 무한히 돌릴 수 없기에 확률적으로 반복 횟수를 결정한다. RANSAC 반복횟수를 N, 한번에 뽑는 샘플 개수를 m, 입력 데이터들 중에서 inlier의 비율을 \(\alpha\)라 하면 N번 중 적어도 한번은 inlier에서만 샘플이 뽑힐 확률은 다음과 같다.
-> RNASAC은 지지하는 데이터 개수가 가장 많은 모델을 뽑는 파라미터 추정 방법이다. 지지하는 데이터는 추정된 모델과 가까이 있는 데이터들을 말한다. 그렇다면 얼마나 가까워야 그 모델을 따르는 데이터라고 간주하는 것일까?
-> RANSAC 알고리즘에서 데이터 \((x_i, y_i)\)와 모델 f와의 거리 \(r_i = |y_i - f(x_i)|\)가 T 이하이면 그 모델을 지지하는 데이터로 간주한다.
-> 문제는 이 파라미터 T를 우리가 결정해줘야 한다. T를 선택하는 가장 좋은 방법은 정규분포를 바탕으로 분산을 \(\sigma^2\)이라 할 때, \(T = 2\sigma 또는 T = 3\sigma\)로 잡는 것이다.4) Hough-Transform
- 이미지 공간을 허프 파라미터 공간으로 변환한다.
- 허프 변환에서는 원래는 포인트에서 허프 공간에서는 라인으로 변한다.
-> 이미지 스페이스(직선) -> 파라미터 스페이스(점)
-> 이미지 스페이스(한 점) -> 파라미터 스페이스(직선)
-> 이미지 스페이스(두 점) -> 파라미터 스페이스(두 직선의 교점)
- 단점은 노이즈에 영향을 많이 받는다.
-
- point cloud로부터 라인을 어떻게 찾을 것인가?