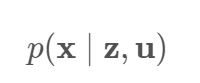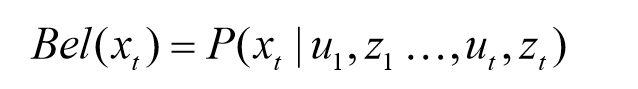Motion and Sensing

Contents

1. Probabilistic Robotics
2. Probabilistic Motion Models
3. Probabilistic Sensor Models

1. Probabilistic Robotics

• Perception = State estimation
  • 어떠한 정보가 주어질 때, 참인 확률(문을 열기 위한 정보에서, 문이 열려있는지의 확률)

  • P(open

    z): 판단, P(z

    open): 원인

  • likelihood(가능성) -> bayes rule
  
  
  • State estimation은 로봇에 주어지는 입력과, 로봇의 센서로부터 얻어지는 데이터로부터 현재의 로봇의 위치인 state와 주변환경에 대한 지도를 추정 방법이다.
  • x 는 로봇의 위치 및 지도(주변의 land mark들의 위치)를 의미하는 vector이며, z는 로봇의 센서로부터 얻어지는 데이터로 observation이라고 부르며, u는 센서의 움직임을 제어하는 입력으로 control input이라고 부른다.

  • State estimation에서 P(open

    z)는 diagnostic하고, P(z

    open)은 causal이다. Causal은 생각보다 구하기가 쉽다.

  
  
• Combining Evidence
  • evidence가 measurement
  • 문이 열려있는 지의 확률은 measurement의 값이 추가적으로 들어옴에 따라 계속해서 바뀜 -> 재귀적 baysian updating을 해준다.
  • 마르코프 추정 - n번째의 measurement는 이전의 (n-1)번째의 measurement에 대해서만 영향을 받는다. zn은 z1, z2, …, zn-1에 대해 독립적이다.
• Action = Utility optimization
  • 행동이 이루어지는 world는 dynamic함
  • 행동은 절대적인 확신을 가지고 수행되지 않음 -> 할 때마다 불확실성이 달라질 수 있음.
  • 센서 모델(절대적인 확신성을 가지고 있음, 신뢰도가 명확함)과 액션 모델(1m를 간 것과 5m를 간 것의 위치 정보는 확연히 차이가 남, 신뢰도가 불확실함)의 차이
  • 오차를 보정해주지 않으면 불확실성이 계속해서 증가하게 된다.
• Modeling Actions

  • 현재와 이전의 액션 상태를 가지고 만든 확률은 P(x

    u, x’)

  • 위의 액션 모델의 확률은 x’에서 x로의 상태로 변하기 위한 u의 변화를 의미하기 때문에 확률밀도함수(PDF, Probablitic Destination Function)로 표현한다.
• State Transitions
  • continuous case - total probabilty - 닫혀있을 확률(u) = 열려있을 때 닫힐 확률 + 닫혀있을 때 닫힐 확률
• Bayes Filters: Framework
  • 주변 환경을 이용해서 로봇의 상태를 역으로 추정하는 measurement 등이 있음

  • 주어지는 것: 센서 모델 P(z

    x), 액션 모델 P(x

    u, x’) - 이전 상태에 대한 현재의 상태, Prior 확률

  • 원하는 것: 동적 시스템의 X에 대한 상태를 추정하는 것, 이벤트들이 동작한 이후의 사후 상태들(Belief)
  
  
  
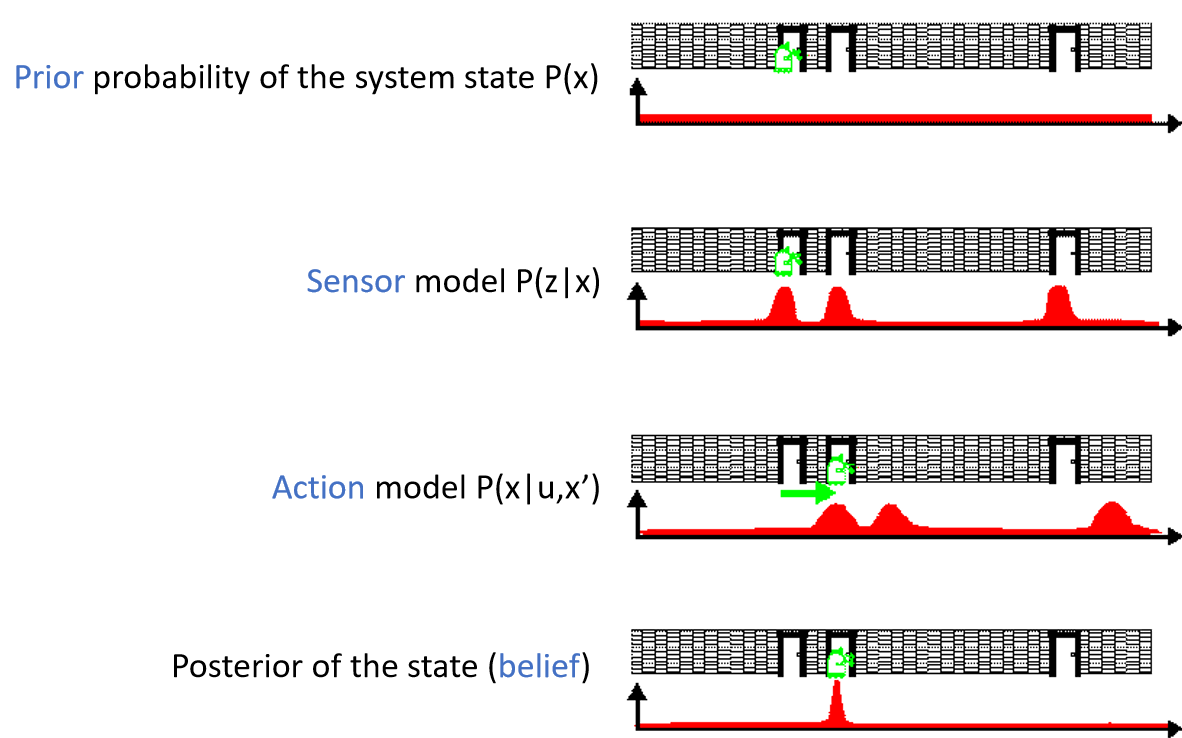
  • prior: 모든 위치에 있다고 가정할 수 있음
  • sensor: 문이 열린 곳에 센서가 작동
  • action: 로봇이 직접 움직이면서 확인, 살짝 certainty가 떨어짐(동작이 있으므로)

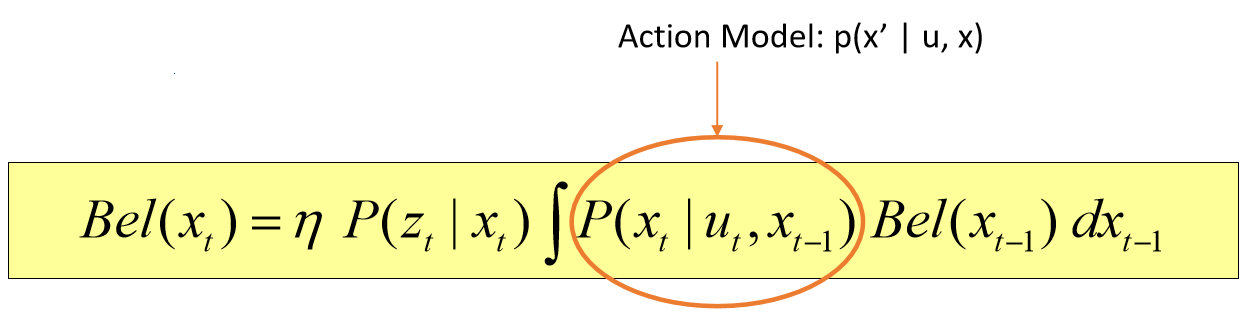
  • belief: 센서 모델 x 액션 모델

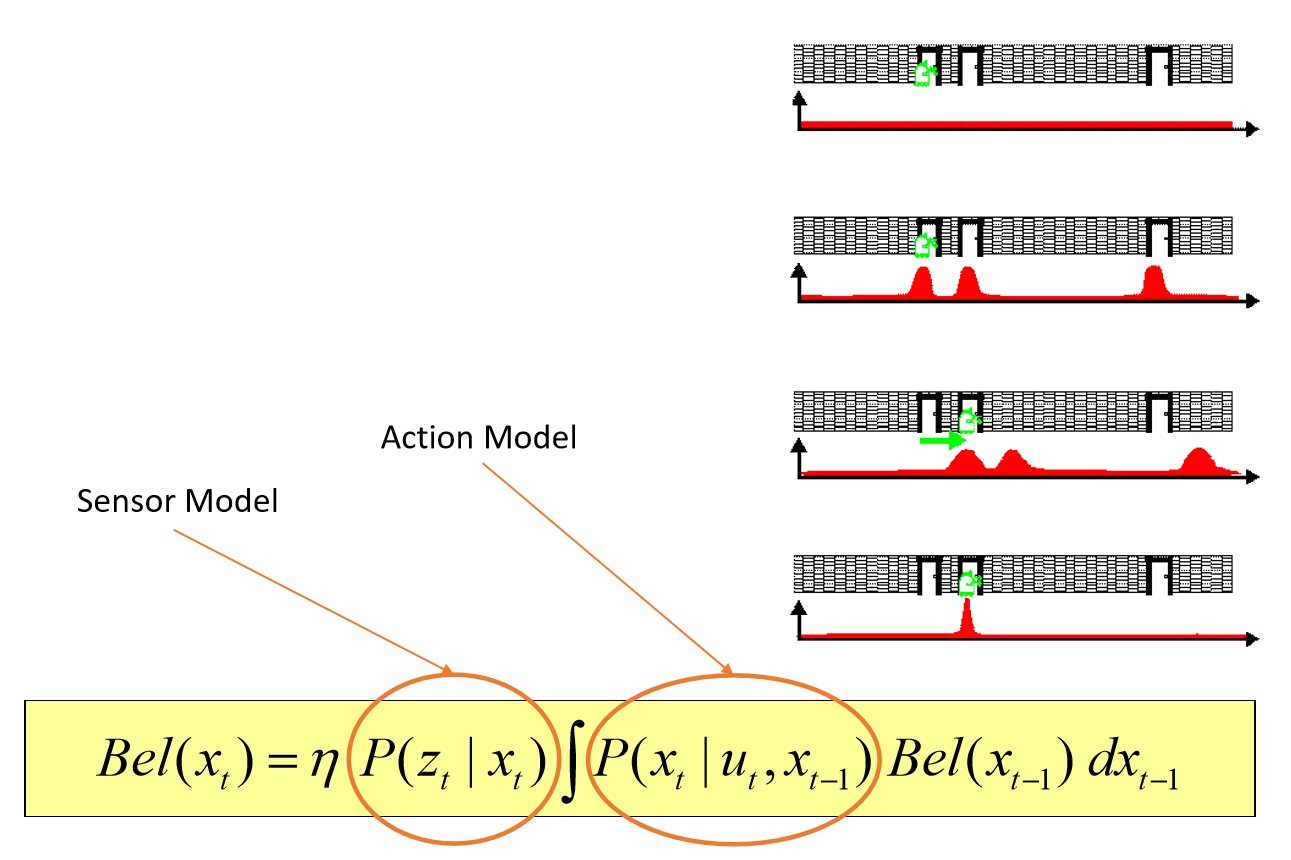
  • Bel(xt) = 이전의 상태(prior 모델)를 바탕으로 현재 상태를 추정(액션 모델)하고, 여기에 추가적으로 입력되는 measurement(센서 모델)를 곱하는 것

    • 센서 모델이 왜 likelihood인지? 사전 정보가 없는 초기 상태에서 시작하기 때문에 추정으로 센서 모델과 이전 상태의 값을 곱하면 사후 확률이 되는 것임
    • 액션이 주어지면서 상태의 값이 바뀌면서 최종적인 현재의 belief값이 구해짐
  
  

2. Probabilistic Motion(Action) Models

• Typical Motion Models
  • Odometry-based model
    • Odometry 기반 모델은 시스템에 휠 엔코더가 장착 된 경우에 사용된다.
    • 노이즈 모델: 현실적으로 노이즈(에러)가 있음
  • Velocity-based model(dead reckoning)
    • 휠 엔코더가 제공되지 않은 경우 Velocity 기반 모델을 적용해야 한다.
• Odometry Model

• Noise Model for Odometry

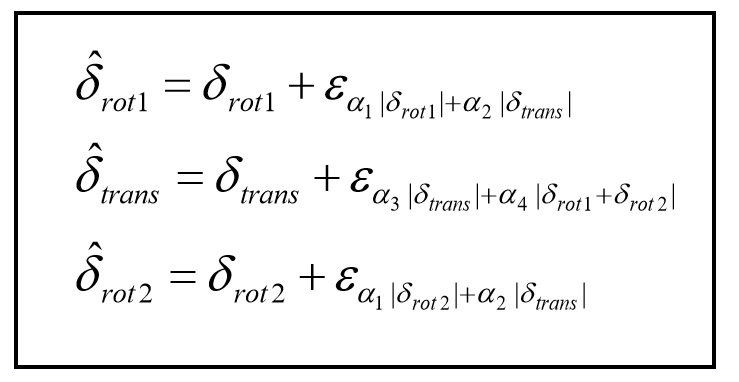
• x, x’, u가 주어졌을 때, 사후 확률 계산

3. Probabilistic Sensor Models

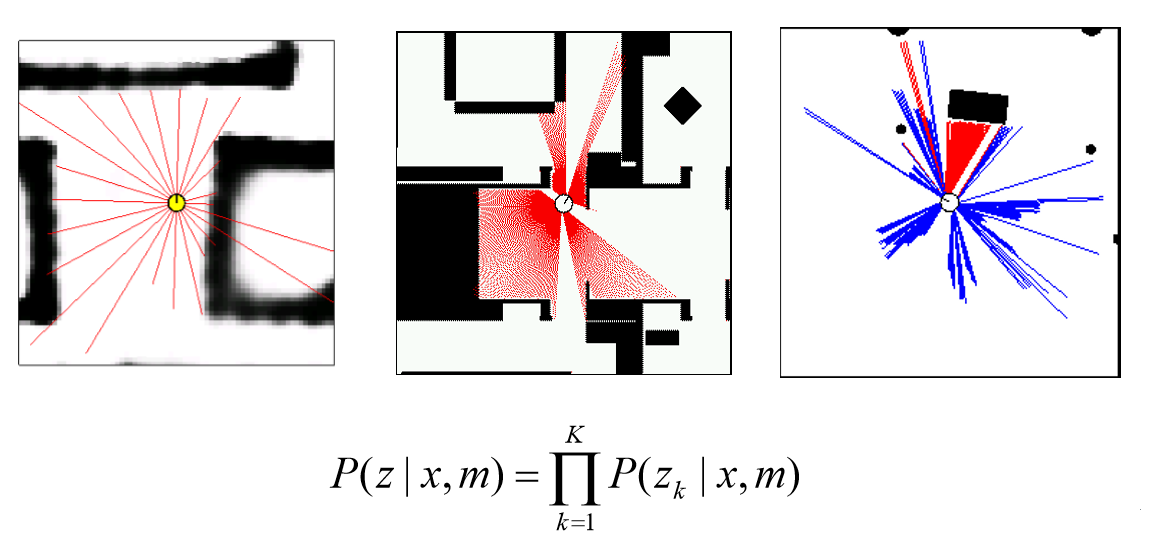
• 위치 x에 따라 측정되는 z에 대한 확률값: p(z

  x)

• Beam-based Sensor Model
  

  • P(z	x, m) - m은 map, 지도상에서 ray로부터 얻어지는 measurement를 가져오면서 실제값과 얼마나 차이가 나는 지를 확인

  • measuremet는 측정값이기 때문에 noise가 있다고 가정할 수 밖에 없기 때문에, 가우시안으로 noise를 잡는다.
  • 불확실한 장애물이 있게 된 경우에도 불확실성이 증가
  • 장애물이 있는 경우의 불확실성과 같은 기본적인 베이스의 불확실성: random measurement