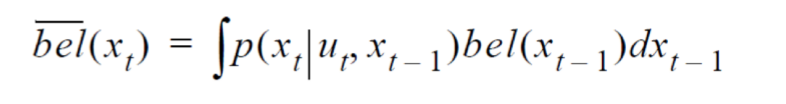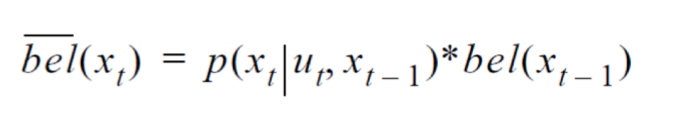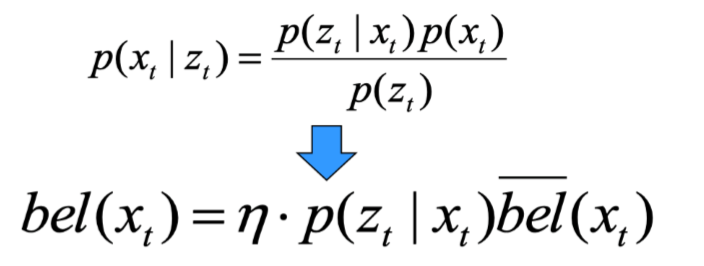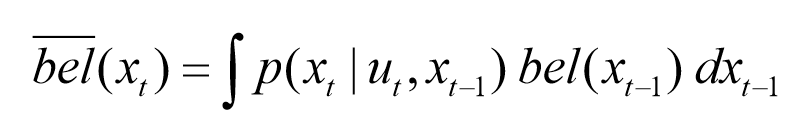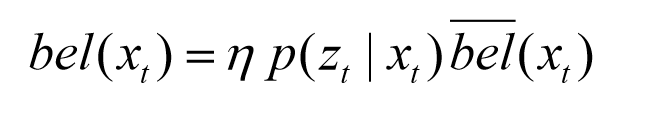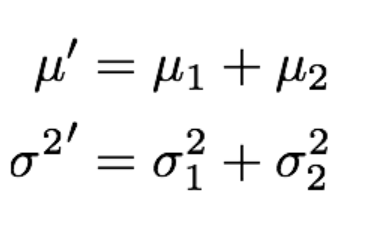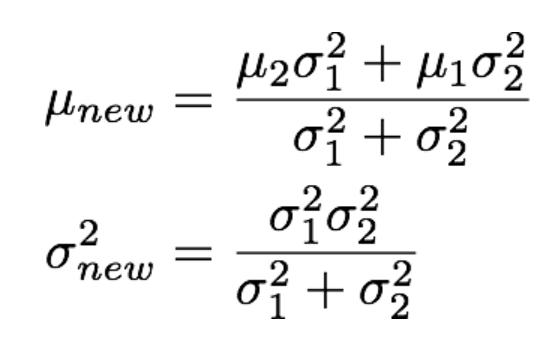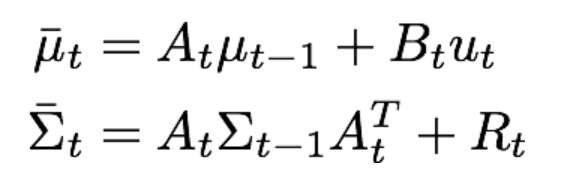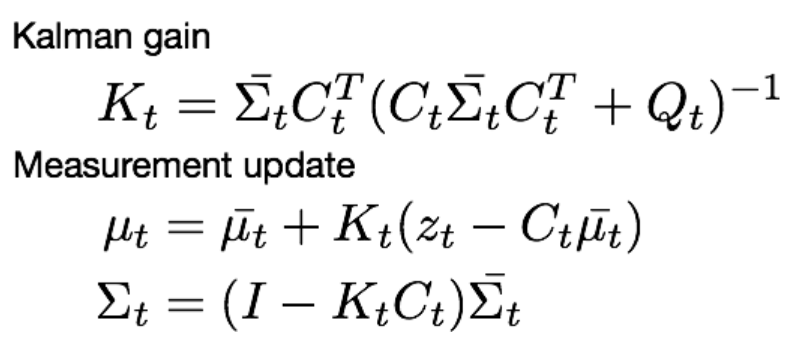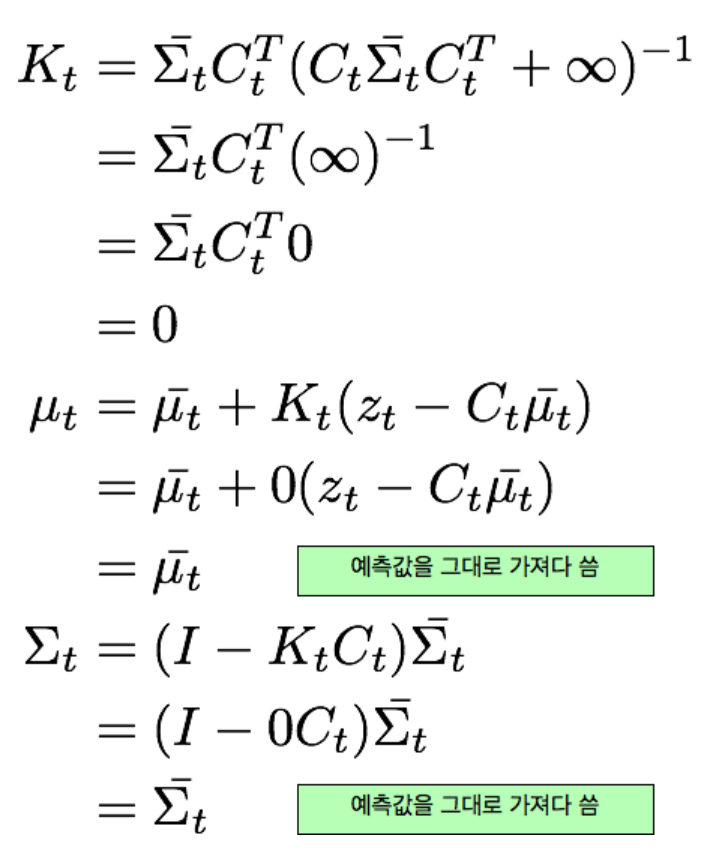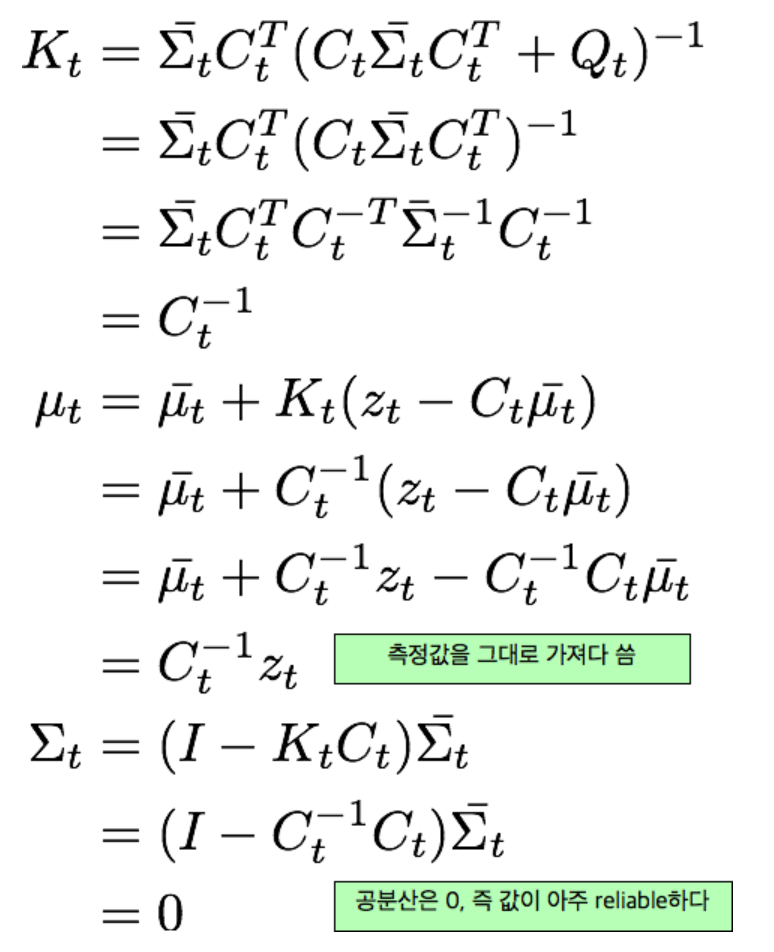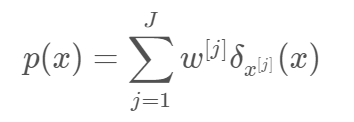Mobile Robotics and ROS [Day 7]

Published On July 11, 2020

Kalman Filter
Extended Kalman Filter
Monte Carlo Filter

Maps

Introduction of maps
Grid based representation
Topological Representation

1. Introduction of maps

localization, path planning, obstacle avoidance
- map이 필요
- 동시에 map 생성과 localization이 가능하도록 -> SLAM
아직까진 불완전함
type of map 1) grid map - 환경을 격자로 나눔. 위치 정보로 표현. 직관적으로 확인이 가능하지만, cell이 모든 정보를 담지는 못하기 때문에 구체적이지는 않음.
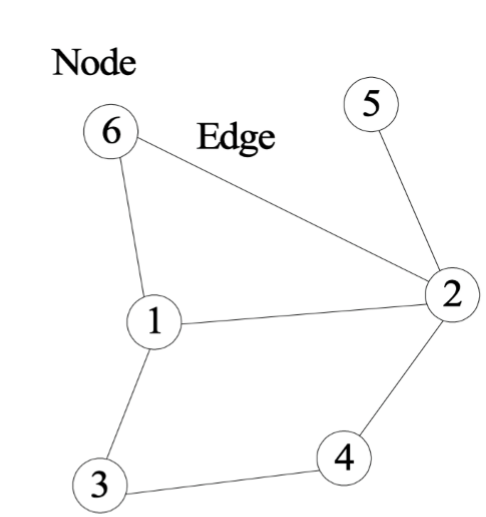
2) topological map
- 노드와 엣지로 구성된 맵. graph 형태. 주변 환경들과 차이가 많이 나는 것을 노드로 표현.
- 에지를 이용해 연결성을 표현. grid map에 비해 리소스가 적게 소요.
- graph searching 알고리즘을 사용하여 위치 정보를 파악.
- 정보들이 축약되어 있는 형태이기 때문에 정확하지는 않음. 3) feature map
- continuous 환경에서 얻어지는 특징들을 위치 정보로 표현. 문제는 확보된 특징이 얼마나 좋고, 강인한 특징일지 확신할 수 없음.
- 마찬가지로 grid map에 비해 리소스가 적게 소요.

2. Grid based representation

occupancy grid representation
- 2D나 3D의 그리드 셀로 분할
- 각 셀은 0과 1사이의 값으로 표현하여 확률(probability)처럼 표현
- 1: occupied, 0: empty, 0.5: unknown => 점유 확률이 1에 가까워질수록 occupied 된다고 인식함
- 센서 모델을 확률적으로 표현하여 얻은 값을 bayesian 모델을 사용하여 각 셀의 확률을 구한다.
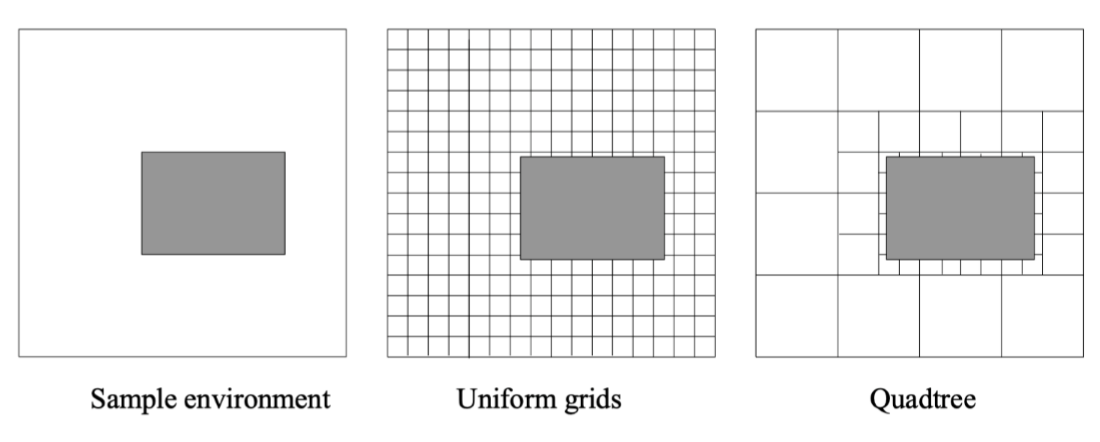
uniform grids vs quadtree
- 장애물과 같은 물체들이 많은 셀의 경우 작게 설정하여 resolution을 적게 만들어줌.
- 점유되는 셀들만 표현하여 리소스를 줄일 수 있음
- 장점: generality
- 단점: 셀의 사이즈가 제한됨.
uniform grids
- 자식 객체들의 갯수에 따라 균일하게 정렬하는 객체
quadtree
- 대량의 좌표 데이터를 메모리 안에 압축해 저장하기 위해 사용하는 여러 기법 중 하나
- 주어진 공간을 항상 4개로 분할해 재귀적으로 표현
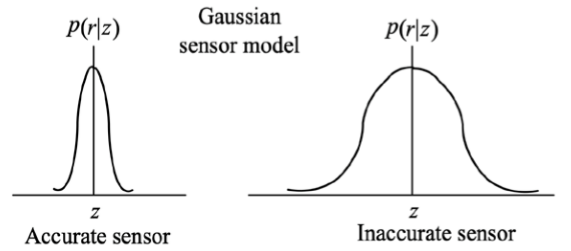
Occupancy grid map using Sensor Model 1) Gaussian Sensor model
- 센서값이 정확하면 variance가 작아지지만, 정확하지 않으면 variance가 커진다.
2) Occupancy Grid Map
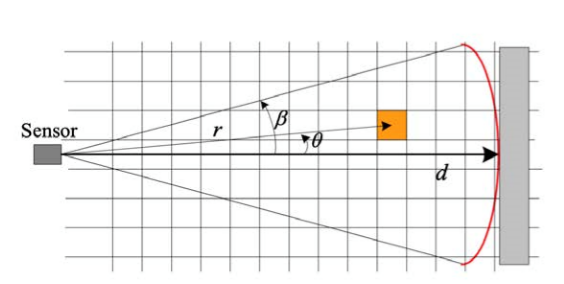
- corn 형태로 모델링하며, 셀들에 대해 점유 확률을 갱신할 수 있도록 만든다.
- range가 d인 경우, 중간에 있는 셀들은 empty되어 있을 확률이 높다.(센서의 값이 도달하지 못하여)
Occupancy Grid Map
- 점유 확률은 셀의 현재 점유 확률 및 새로운 범위 데이터로부터 업데이트 됨.
- 베이지안 모델로 업데이트
- 장점
  - 최단 거리 계산 유용
- 단점
  - 비슷한 환경이 많은 데, 동일한 셀들로 나누기 때문에 리소스가 많이 차지함.
  - 환경의 복잡성에는 영향을 받지 않음(그저 해당 셀이 점유가 되어 있는지 여부에 따라 결정).
  - 그리드 맵을 만들기 위해선 많은 메모리가 잡아먹는다(모든 위치 정보를 가져와서 맵을 구성하기 때문에).
  - 최근에는 topological 맵 처럼 구역을 나누어서 리소스를 줄여나가고 있음.

3. Topological Representation

각 위치의 연결성을 설명해주는 에지와 함께 discrrete 위치(node or vertex로 표현)에 대한 환경을 추상화시킴.
그래프 형태(노드와 에지) -> 인접행렬
에지: 노드와 노드 사이의 거리 정보는 없고, 단지 연결성만 가지고 있음
SLAM에서 주로 사용하는 topological 방법
- 상대적 위치를 계산. 영상에서 키 프레임을 노드로, 키 프레임과 키 프레임 사이를 에지로 구성.

Localization

Introduction
Map-based Localization
Kalman Filter Localization
Monte Carlo Localization

1. Introduction

localization
- global reference frame의 관점에서 로봇의 pos(위치와 방위)를 정의하는 것
- global reference frame: 지도의 기준 좌표
Difficulty of localization
- 불확실성
- 단일 센서로 측정한 값들이 효율적이지 않음. -> 하지만 요즘은 Lidar를 이용해서 측정하고자 함.
- 여러 가지 변수를 이용해서 pos를 구해야 한다!
given
- 환경에 대한 지도가 주어짐
- 센서 정보들이 주어짐
wanted
- 로봇의 pos를 추정하고자 함
해결해야 할 이슈
- 시간에 따라 pos가 어떻게 변하는지 추적(tracking)
- 전역적으로 pos의 위치가 어딨는지
- 로봇을 이상한 곳에 두어도, 자기 위치 정보를 정확히 파악할 수 있는지
global localization
- 초기 정보를 알려주지 않음(기준이 계속 바뀔 수 있음) -> 처음에 대략적인 가정을 가지고 시작함.
position tracking
- 계속적으로 odometry로 에러를 줄여나가야 함

2. Map-based Localization

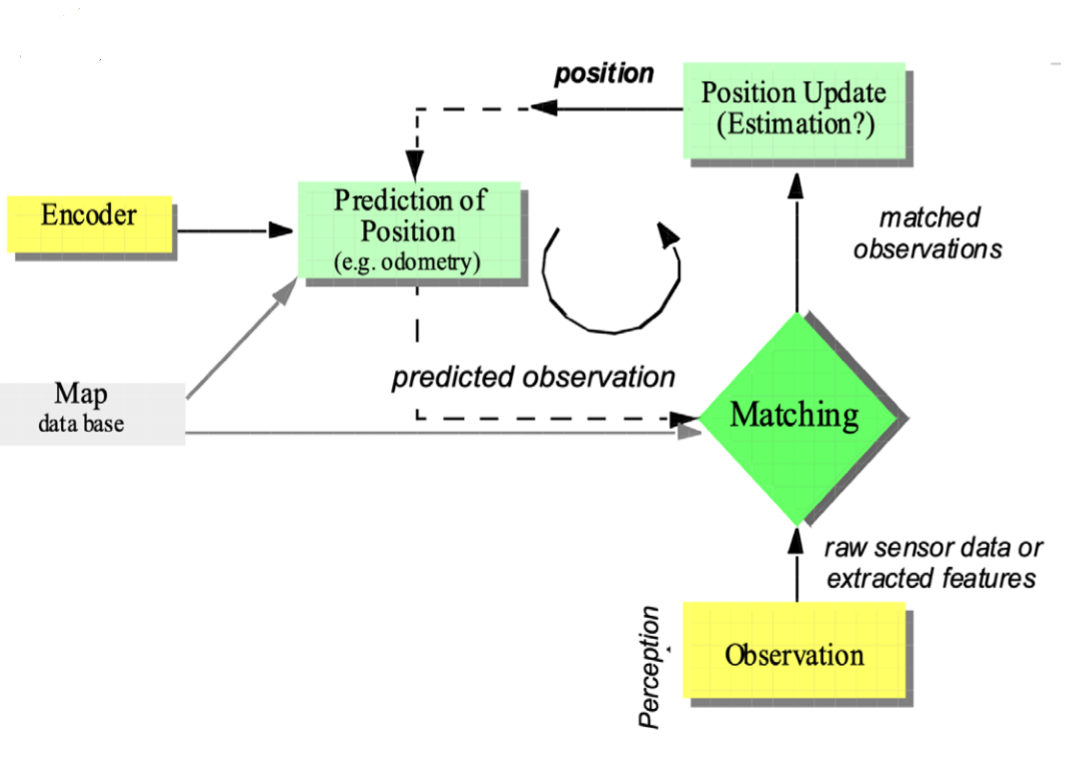
불확실한 정보는 그 위치에 대해서만 자기 위치에 대한 센서 정보 및 local 정보를 비교하면서 불확실성을 줄여나감
Map-based Localization을 위한 필요사항
1) Position estimation(odometry)
- 속도, 이동량 등의 값을 추정하는 단계
- odometry로 계산을 계속하다 보면 에러가 누적될 수 있음
  - 헤딩 센서가 있다면 누적 에러값을 줄여줄 수 있지만, 원천적으로는 힘들다.
- 입력되는 값: x, y, theta
  - prediction 2) Error (uncertainty) propagation
- 오차를 어떻게 모델링할 것인지
  - 이동량에 비례해서 왼쪽 바퀴와 오른쪽 바퀴의 에러값의 누적합
  - 자코비안 메트릭스로 구할 수 있다
3) Position representation 4) Map representation
Probabilistic Map based Localization
- 두 가지 방법 1) Markov localization 2) Kalman filter localiztion
- 문제
  - 정확히 알려진 위치에서 이동하기 시작하면 휠 주행 거리계를 사용하여 위치를 추적 할 수 있다. 그러나 특정 움직임 후 로봇은 그 위치에 대해 불확실성이 발생한다. 따라서 환경을 관찰하여 위치를 업데이트해야 한다.
  - 실제 로봇의 위치를 최대한 업데이트 할 수있는 odometric 추정.
- Description of the probabilistic localization problem
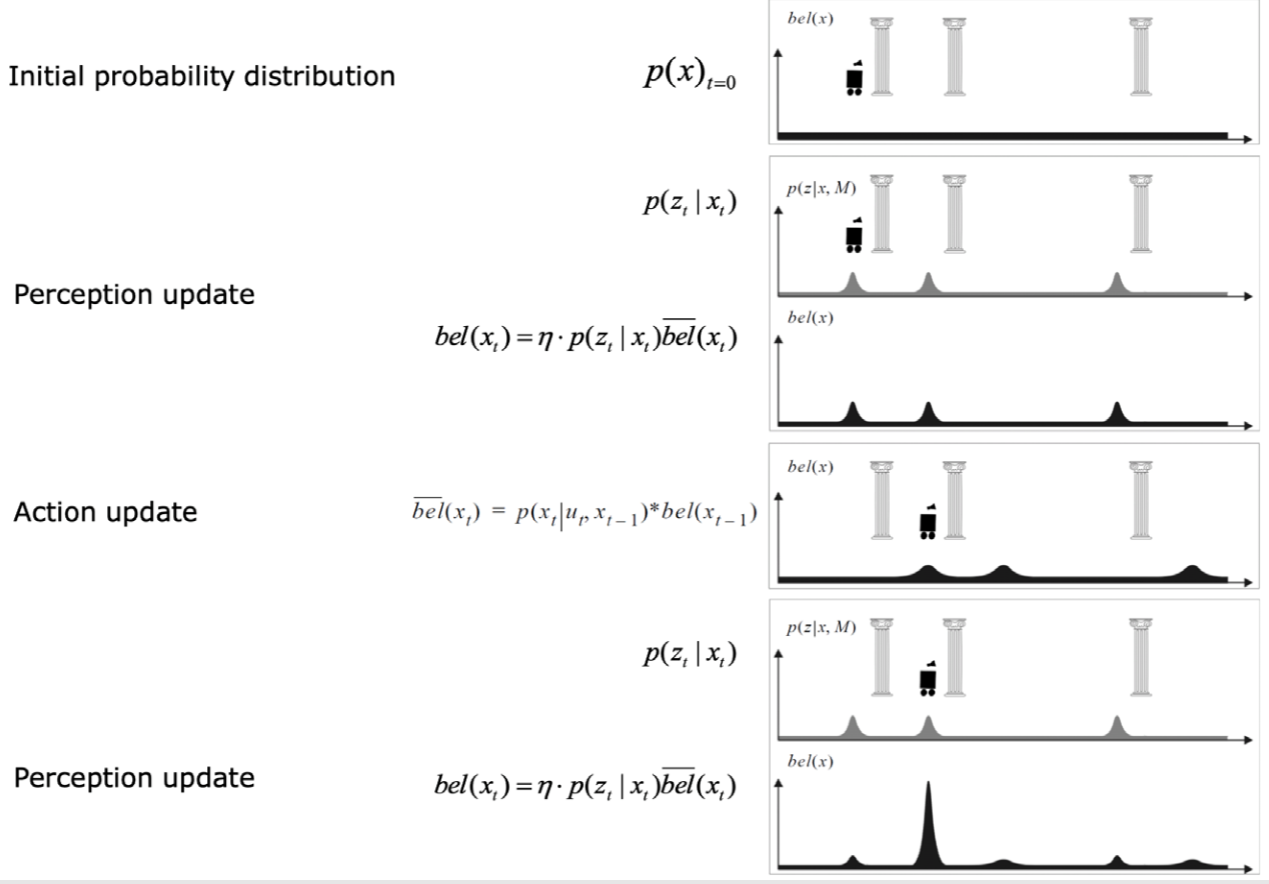
  - action(prediction)이 업데이트될 때 불확실성의 증가
  - 마르코프 가정(Markov Assumption)은 확률변수의 총 시퀀스가 주어졌을 때, 어떤 확률변수 \(X_t\)의 분포는 바로 직전에 나타난 확률 변수 \(X_(t-1)\)에만 의존한다는 것이다.
  - 이러한 가정을 전제로, odometric 입력 \(u_t\)와 이전의 위치에 대한 정보 \(bel(x_(t-1))\)을 기반으로 현재 위치에 대한 정보 \(bel(x_t)\)를 추정한다.
  - 위의 수식을 교차 관계(cross-correlation)을 적용하면 다음 수식과 같다.
  - 로봇의 움직임에 따른 베이지안 확률을 넣으면 다음 수식과 같다.
- prediction
- correction

3. Kalman Filter Localization

칼만필터 알고리즘의 2가지 가정
- 모션 모델(로봇이 현재 위치에서 모션 입력을 받아 움직였을 때의 확률 모델)과 측정 모델(로봇이 현재 위치에서 자신이 가진 센서를 이용해서 자신이 어디에 위치해 있는지를 측정했을 때의 확률 모델)이 linear한 시스템
- 모션 모델과 측정 모델이 Gaussian 분포를 따르는 경우
- 위의 2가지 가정이 만족되면 optimal이 보장된다.
칼만필터의 2가지 단계(prediction, correction)
- 상태 예측(state prediction)
  - 이전 로봇의 파라미터(위치, 속도 등)와 로봇 모션 입력을 이용해 현재 로봇 파라미터 값을 예측하는 단계
- 측정 업데이트(measurement update)
  - 상태 예측단계에서 예측된 현재 로봇의 파라미터 값과 현재 로봇의 위치에서 얻어진 센서 정보(실제값)를 이용해 현재 로봇 파라미터 값을 업데이트하는 단계
- 위의 2가지 단계를 반복적으로 수행하며 로봇의 현재 위치를 계산한다.
1차원
- 상태 예측(prediction)
  - 이전 측정 업데이트(correction)에서 계산한 확률 분포와 로봇 모션 입력의 확률 분포를 이용해 현재 상태의 분포를 예측한다.
  - 이 때 확률 분포의 평균은 간단히 두 평균을 더한 것이고, 확률분포의 분산은 두 분산을 더한 것이다.
- 측정 업데이트(correction)
  - 상태 예측단계에서 예측된 현재 로봇 위치에 대한 확률 분포와 현재 로봇의 위치에서 측정한 관찰값의 확률분포를 이용하여 사후 확률분포를 업데이트하는 방식
  - 확률분포는 가우시안을 따름.
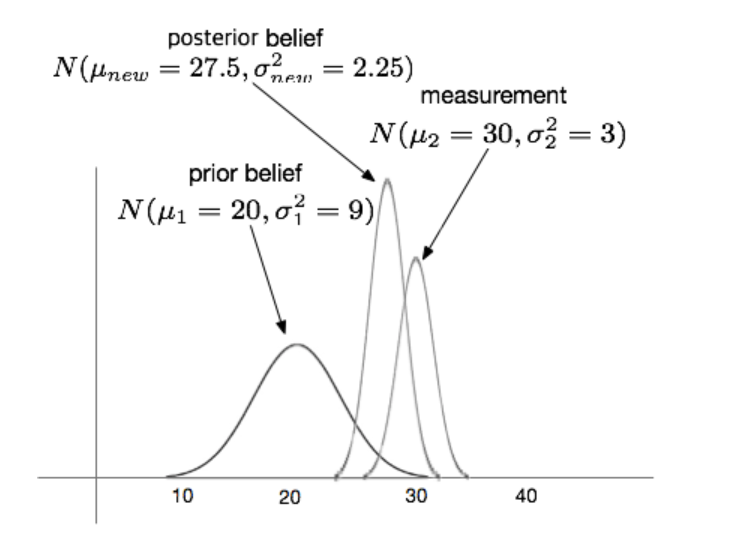
  - 업데이트 되는 가우시안 확률 분포는 이전 가우시안 분포와 측정값의 가우시안 분포의 곱으로 구할 수 있다.
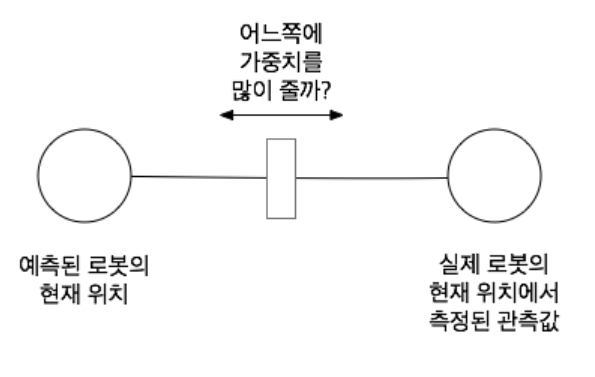
  - 이전 상태 예측단계에서 예측된 로봇의 현재 위치와 실제 로봇의 현재 위치에서 측정된 가중치를 이용해 측정값을 업데이트 한다.
  - 여기서 가중치는 예측된 로봇의 현재 위치에 대한 분산값과 실제 로봇의 현재 위치에서 측정된 관측값의 분산값에 따라 결정된다.
  - 이 가중치는 다차원의 경우에 칼만게인이라는 행렬로 확장된다.
다차원
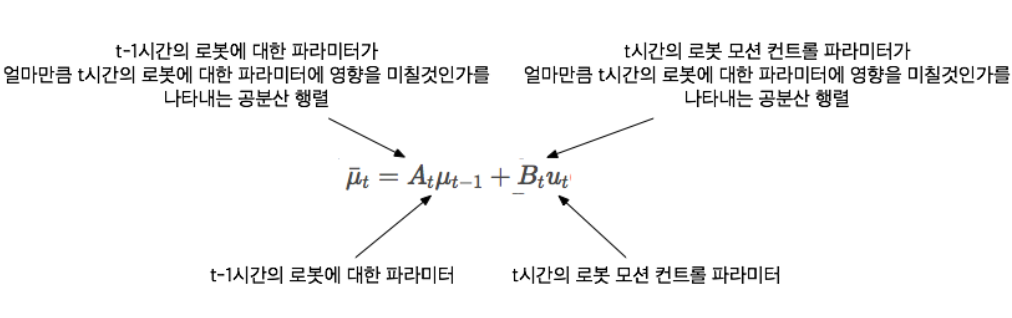
- 상태 예측(prediction)
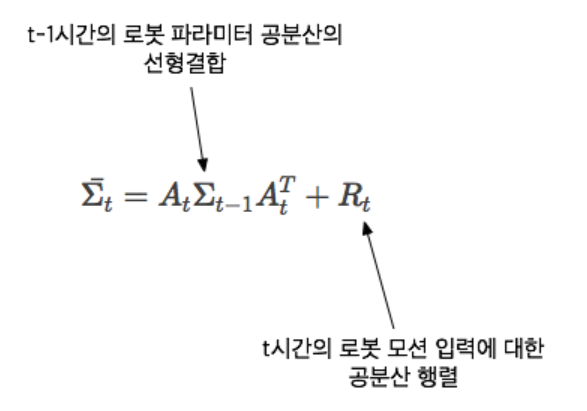
  - 이전의 로봇 파라미터에 대한 확률 분포에 로봇 모션 입력의 확률 분포를 더해준다.
  - 공분산 행렬은 베어링 마찰이나 공기저항 등
- 측정 업데이트(correction)
  - 이전 상태 예측단계에서 예측된 로봇의 파라미터 값과 현재 로봇의 상태에서 측정한 파라미터 값 사이를 가중치를 이용해 측정값을 업데이트
  - 여기서 가중치는 칼만게인으로 정의되며, K로 나타냄.
  - 공분산인 Q가 측정하기 어려운 경우(무한대), 칼만게인의 값은 0이 되면서 예측값을 그대로 사용한다.
  - 반대로 Q가 측정이 잘되어 신뢰도가 높은 경우(0), z값만 남게되어 측정값을 그대로 사용한다.
확장 칼만필터(Extended Kalman Filter)
- 가우시안 분포를 가정한다.
- 칼만필터는 선형 가우시안 모델이라면, 확장 칼만필터는 비선형 가우시안 모델이다.
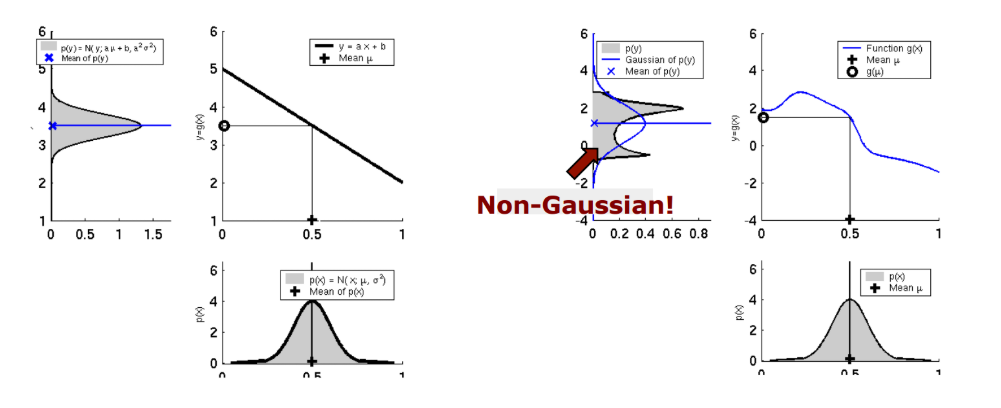
- 비선형 모델은 다음 그림과 같은 문제가 발생한다.
- 많은 system에서 Gaussian 분포를 사용하는 이유는 평균(mean)과 분산(variance) 두 개의 파라미터로 분포를 표현함과 동시에 데이터들의 분포를 정확히 반영할 수 있기 때문이다.
- 따라서 반복적인 계산을 통해 state를 추정하는 문제에서 입력이 가우시안 분포일 때 출력 또한 가우시안 분포이어야 한다.
- 하지만 위의 그림과 같이 비선형 시스템인 경우, 입력은 가우시안 분포이지만 출력은 가우시안 분포가 아니다. 따라서 이런 경우 출력을 평균과 분산으로 표현할 수 없다.
- 이를 해결하기 위해 비선형 함수를 선형화(linearization) 시키는 과정이 필요하다.
Linearization(선형화)
- EKF에서 비선형 함수를 선형화시키기 위해서는 1차 Taylor 근사법을 사용한다.
- 이때 비선형 함수들을 state로 편미분하여 matrix를 생성하는데, 생성된 두 개의 \(matrix(G_t, H_t)\)를 Jacobian Matrix라고 한다.
Application to the 2D Mobile Robot case
- 측정된 값과 예측된 값의 차이가 있을 경우, h(x)의 센서 모델과 x’(t)의 예측된 모델은 그대로지만, ktVt의 위치가 correction에 의해 조정되면서 x(t)의 값이 조금씩 바뀐다. 그때의 신뢰도인 Pt 역시 또 바뀐다.
- 동기화 주기가 다르다(예측값과 실제값의 유입 주기).

4. Monte Carlo Localization

Particle filters
- 파티클 필터의 목적은 가우시안 분포가 아닌 임의의 분포를 다루기 위한 접근 방법이다.
- 가중치를 갖는 파티큭들의 set은 다음과 같다. \(x^[j]\)는 particle의 위치, \(w^[j]\)는 particle의 weight을 의미한다.
- Posterior(사후 확률)은 다음과 같다.
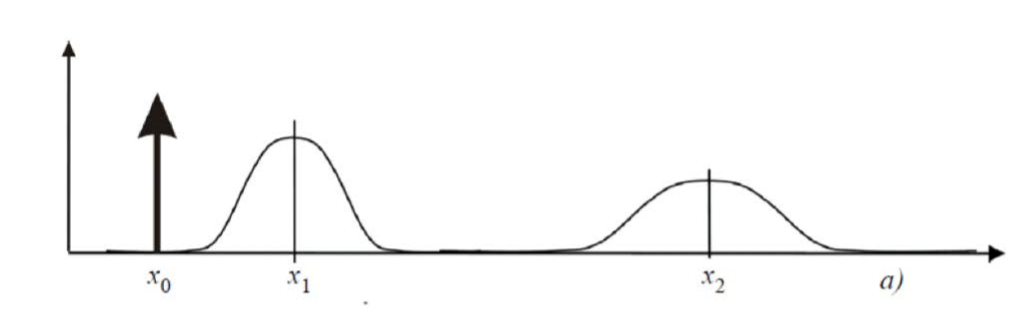
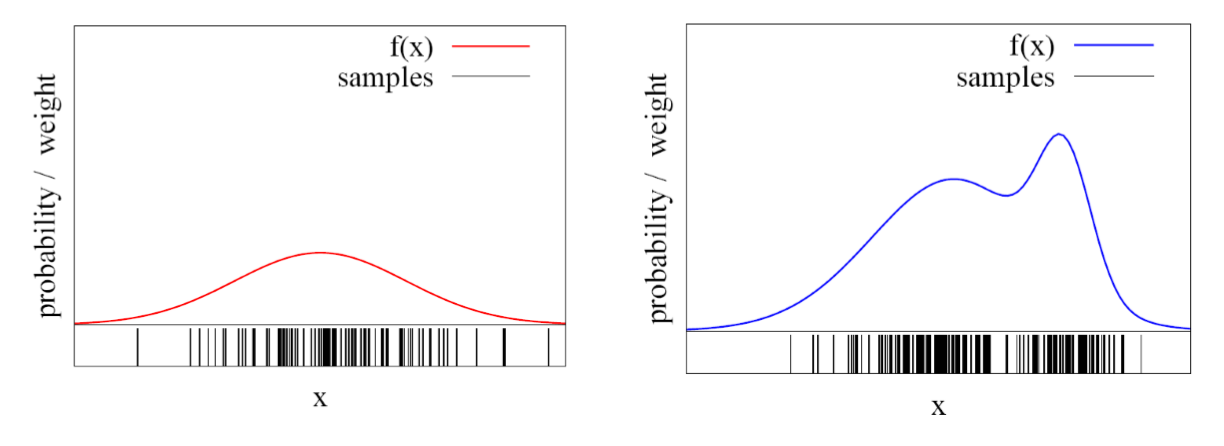
- 파티클 필터가 다음 두 가지의 분산 형태를 갖는다고 가정할 때, 샘플을 어떻게 추출할 수 있을까?
- 왼쪽의 그림은 가우시안 분포를 따르고 있기에 임의의 값을 뽑고 합을 구함으로써 샘플을 추출할 수 있지만, 오른쪽의 임의의 분포는 같은 방식으로 샘플을 추출할 수 없다.
- 따라서 가우시안 분포가 아닐 때의 샘플링하는 방법은 다음과 같은 방법과 알고리즘을 사용한다.
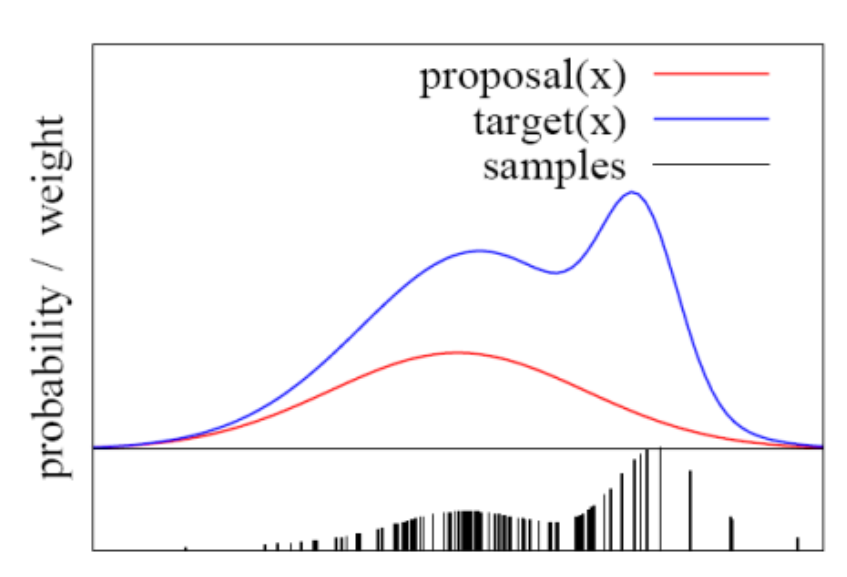
- proposal(x)는 실제 분포인 target(x)를 가우시안 분포로 근사한 함수이다.
  - 하나의 point에 대해서 uncertainty 분포가 구해지면, 그 분포가 proposal distribution이다.
  - 그리고 다시 새로운 예측값이 생길 때, proposal distribution에서 방금 구해진 point가 포함되는 분포가 target distribution이다.
  - 예를 들어, 별의 위치를 예측하여 target distribution이 정해졌지만, 실제로 별의 위치에 obstacle이 없다면 target distribution이 0으로 수렴하므로 importance weight의 값은 0으로 수렴한다.
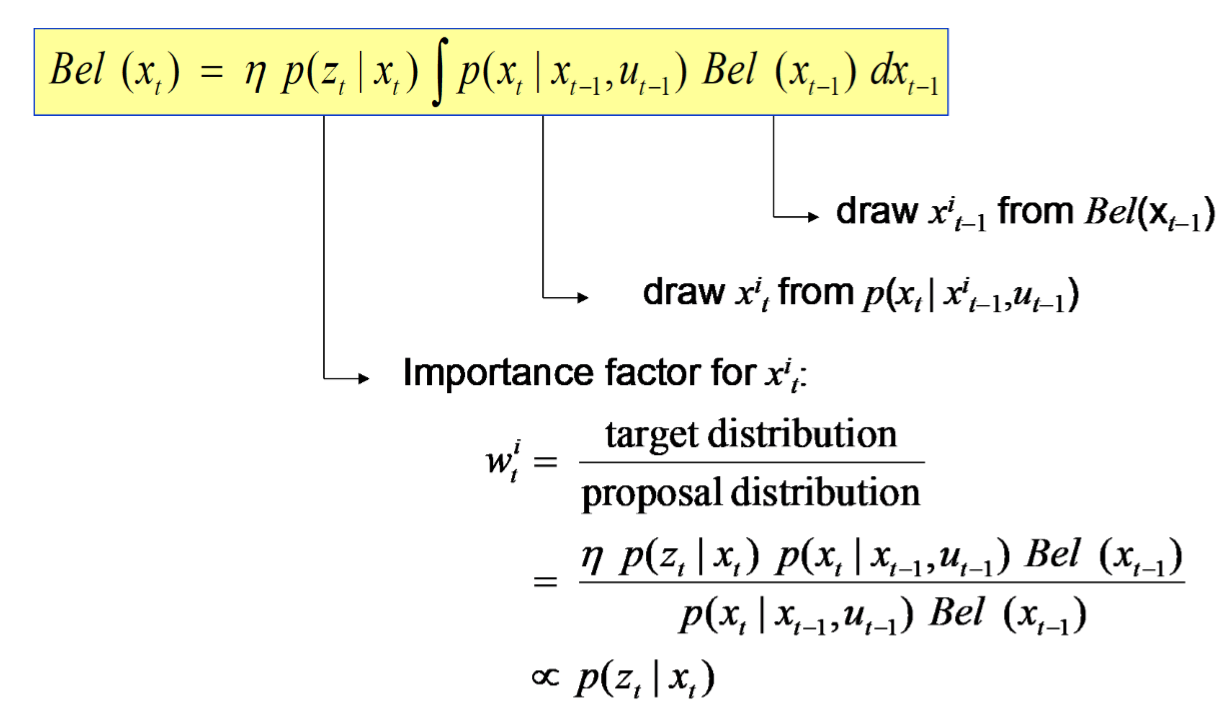
- 위의 알고리즘을 localization에 적용시키면 다음과 같다.
- 샘플을 구하는 3번 라인은 로봇의 모션 모델이 되며, 각 파티클의 가중치는 센서의 observation model이다.
- 7번 라인부터 10번 라인까지는 resampling 과정이다.
  - resampling이란 확률이 작은 파티클은 제거하고, 확률이 큰 파티클은 여러 개로 나눈다.
  - resampling을 하는 이유는 우리가 사용할 수 있는 point의 갯수가 한정적이기 때문에 resampling 전과 후의 particle의 개수는 같아야 한다.
  - 또한, resampling 전에 particle들의 가중치는 다르지만, resampling을 한 후에는 모두 같아진다.
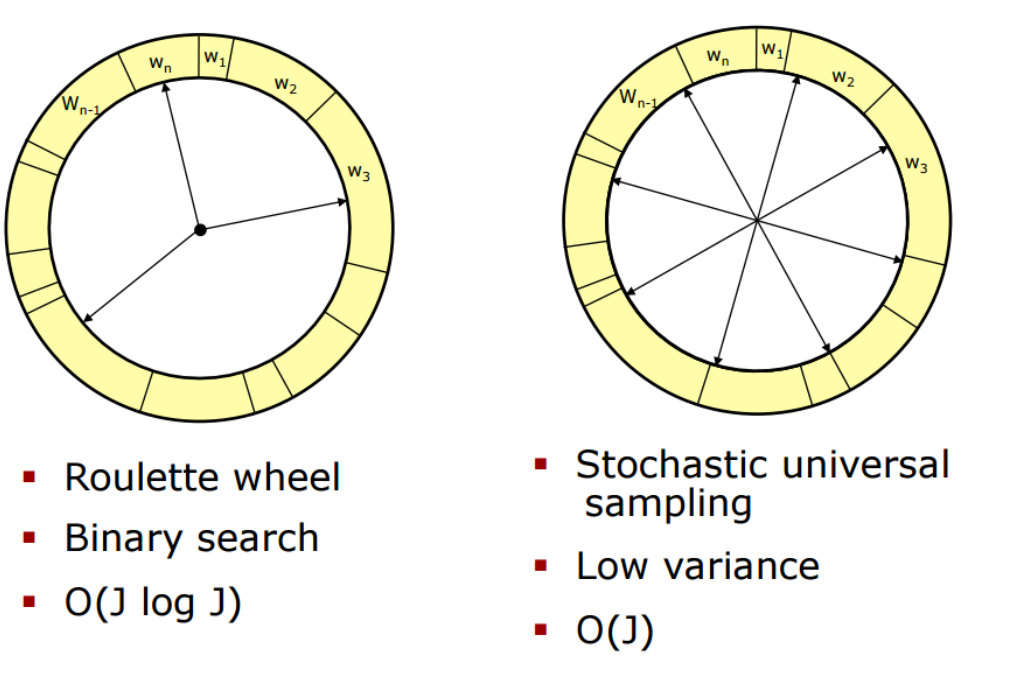
  - 다음은 resampling의 방법들이다.
  - 왼족 그림과 같이 룰렛에서 weight에 따라(한쪽으로 모아두는 경우) 1~1000까지를 나눠서 랜덤으로 뽑을 경우, 운이 나쁘면 weight가 적은 것만 계속 뽑힐 수 있다.
  - 이를 방지하기 위해 오른쪽 그림과 같이 1~1000까지를 고르게 나누고, weight값을 계산하여(각각 다르게) 그 부분을 resampling한다.
- Monte Carlo Filter는 다음과 같이 하나의 주기를 가지며 계속 반복적으로 시행한다.
```
particle sampling -> importance weight 계산 -> resampling
```
정리
- Kalman Filter - 선형 함수 + 가우시안 분포
- Extended Kalman Filter - 비선형 함수 + 가우시안 분포
- Monte Carlo Filter - 비선형 함수 + 임의 분포