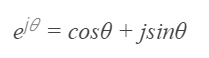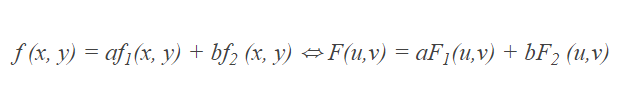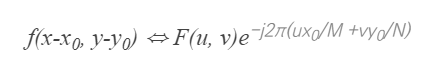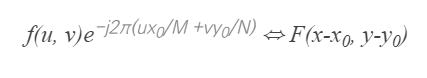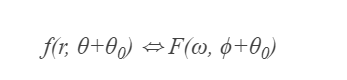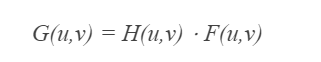Visual C++ 영상 처리 프로그래밍
10. 변환영역 처리 이론 및 실습
10.1. 변환영역 처리 이론
10.1.1. 주파수 영역
- 자연계에서 발생하는 모든 신호는 특정 함수로 표현이 가능하다.
- 지금까지는 공간영역에서의 영상처리를 다루었다. 그리고 이제부터는 공간영역의 문제를 주파수 영역으로 변환하여 다룰 수 있다.
- 주파수란 공간영역에서 밝기나 색상의 변화 정도를 나타낸다.
- 영상의 공간 주파수는 화소값의 변화율을 의미한다.
- 영상으로부터 고주파 성분(주변영역과 색의 차이가 크게 나는 부분)을 제거하면 영상이 부드러워진다.
- 영상으로부터 저주파 성분(주변영역과 색의 차이가 적게 나는 부분)을 제거하면 영상의 경계선이 강조된다.
- 고주파는 가운데로 모이고, 저주파는 모서리 부분으로 모이는 특징이 있다.
10.1.2. 푸리에 변환(Fourier Transform)
- 푸리에 변환은 원래 신호처리 분야에서 시간축에 따른 신호의 세기를 분석하기 위해 연구되었다.
- 즉, 푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는 것이다.
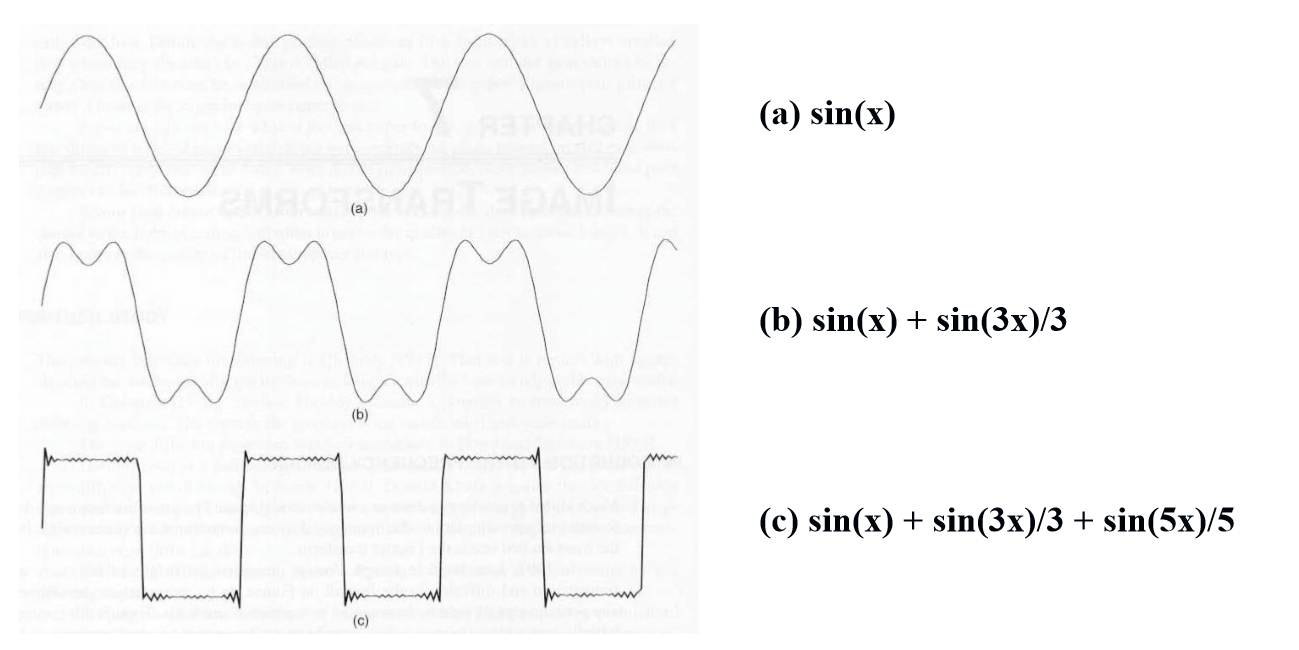
- 임의의 주기적인 신호는 연속된 사인곡선의 조합으로 표현될 수 있다는 이론에 근거한다.
- 푸리에 변환은 sin함수와 cos함수를 기저함수로 사용하여 입력 신호를 변환한다.
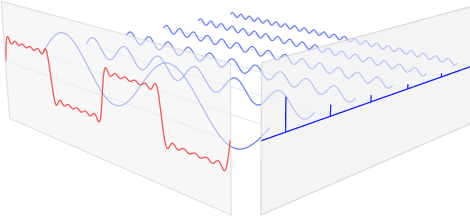
- 아래의 그림과 같이 맨 앞의 붉은색 신호는 입력 신호이고, 뒤의 파란색 신호는 푸리에 변환을 통해 얻어진 주기함수 성분들이다. 각각의 주기함수 성분들은 고유의 주파수(frequency)와 강도(amplitude)를 가지고 있으며, 이들을 모두 합치면 원본 붉은색 신호가 된다.
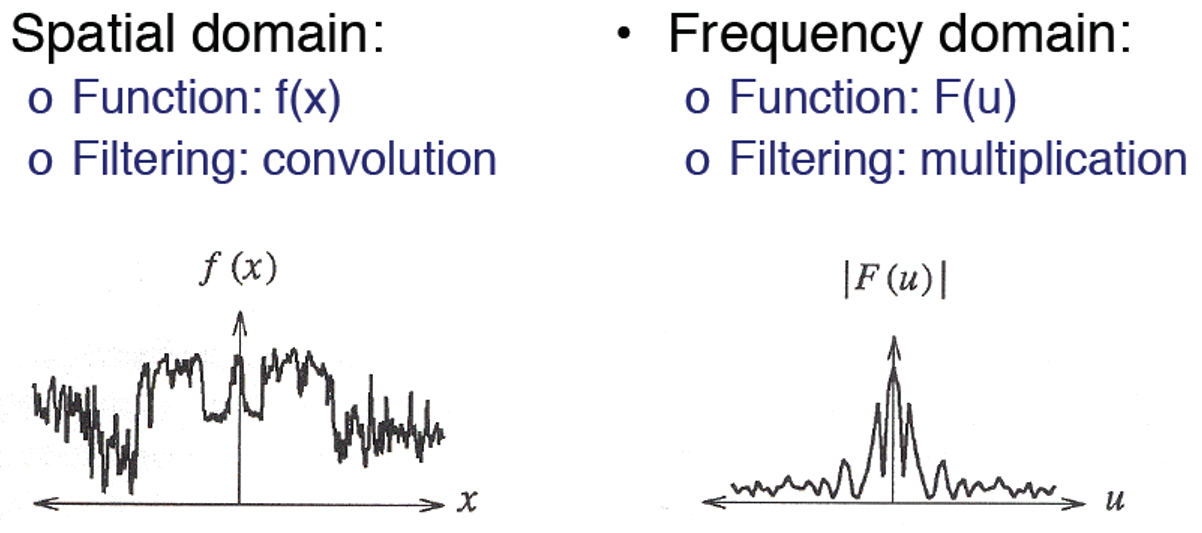
- 영상처리나 컴퓨터 비전에서는 푸리에 변환이 spatial domain(공간 영역)에서 frequency domain(주파수 영역)으로의 변환이라고 부른다.
- 이미지는 연속(continuous)이 아닌 이산(discrete) 신호로, 한정된 유한 구간에서 정의된 신호이다.
- 1차원 데이터에 대한 이산 푸리에 변환(Discrete Fourier Transform)
- 다음은 푸리에 변환 공식에 의해 주파수 공간의 함수로 변환된 이산 신호 함수이다.
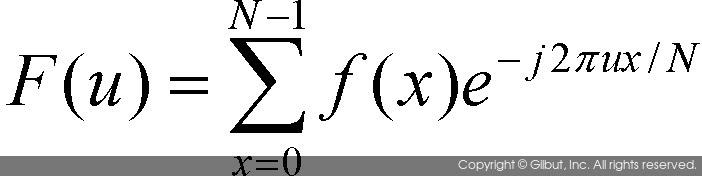
- 주파수 변환에는 주파수 형태의 영상을 공간 형식으로 변환하는 이산 푸리에 역변환(Inverse Discrete Fourier Transform)이 반드시 있어야 한다.
- 다음은 이산 푸리에 변환에 의해 생선된 함수 F(u)를 다시 역변환 과정을 거친 역변환 공싱이다.
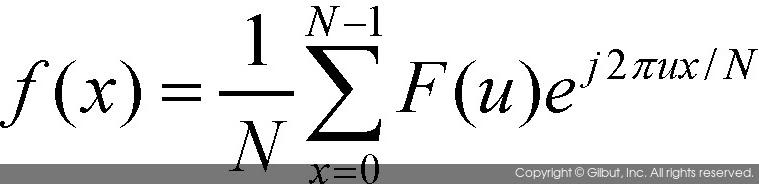
- 푸리에 변환에 의해 생성된 함수 F(u)는 복소수 공간에서 정의된다.
- 푸리에 변환의 공식을 이해하기 위해선, 오일러 공식(Euler’s formula)을 알아야 한다. 오일러 공식은 복소지수함수를 삼각함수로 변환할 수 있도록 하는 유명한 식이다.
- 푸리에 변환을 구할 때는 함수 F(u)의 실수부와 허수부를 따로 고려해서 계산해야 하며, 푸리에 역변환을 이용하여 입력 신호를 다시 복원할 경우에는 실수부만을 이용한다.
- 구해진 복소수는 푸리에 변환의 스펙트럼(spectrum)이라고 하며, 실수부는 푸리에 변환의 위상(phase)이라고 표현한다.
- 푸리에 변환의 관점에서 보면, 스펙트럼은 해당 주파수 성분이 원 신호(이미지)에 얼마나 강하게 포함되어 있는지를 나타낸다.
- 마찬가지로, 위상은 원본 신호를 주기 신호로 분해했을 때 각 주기성분의 시점이 어디인지(각 주기성분들이 어떻게 줄을 맞춰서 원본 신호를 생성했는지)를 나타내는 요소가 된다.
- 2차원 영상에서의 푸리에 변환
- 이산 푸리에 변환 결과를 그레이스케일 영상 형태로 화면에 표현하려면 푸리에 변환 결과값을 0~255 사이의 값으로 변환해주어야 한다.
- 하지만, 영상의 주파수 성분은 복소수 형태를 갖기 때문에 푸리에 결과를 스펙트럼과 위상각을 따로 분리하여 표현하는 것이 일반적이다.
- 실수부와 허수부로 나눠서 할 수 있지만, 스펙트럼과 위상각이 주파수 특성을 더욱 잘 표현할 수 있다.
-
푸리에 스펙트럼을 이미지로 시각화하는 데는 2가지 문제가 있다. 1) 저주파 영역은 매우 큰 값을 갖는 반면에 대부분의 다른 영역은 0에 가까운 값을 가진다. 이러한 문제를 해결하기 위해 로그(log) 변환을 거친다.
2) 원래의 스펙트럼 이미지는 모서리로 갈수록 값이 높아지기 때문에 스펙트럼의 형태를 파악하기 힘들다. 이러한 문제를 해결하기 위해 모서리를 중앙에 오도록 스펙트럼의 위치를 이동시킨(shift) 형태의 이미지를 사용한다. - 영상에 대한 푸리에 변환 결과는 푸리에 스펙트럼이 원점대칭인 주기함수이기 때문에 항상 상하좌우 대칭 형태로 나타난다(입력값이 실수로만 이루어진 경우). 따라서 변환 결과는 가로, 세로 방향으로 영상의 크기 반만큼 이동하여 화면을 출력해줘야 한다(shift 연산 필요).
- 푸리에 스펙트럼의 해석

- 스펙트럼은 해당되는 주파수 성분의 강도를 나타낸다.
- 일반적으로 푸리에 스펙트럼 이미지는 원점 F(0, 0) 주변의 저주파 영역에서 강한 피크가 나타나고, 원점에서 멀어질수록(고주파 영역으로 갈수록) 값이 급격히 작아진다.
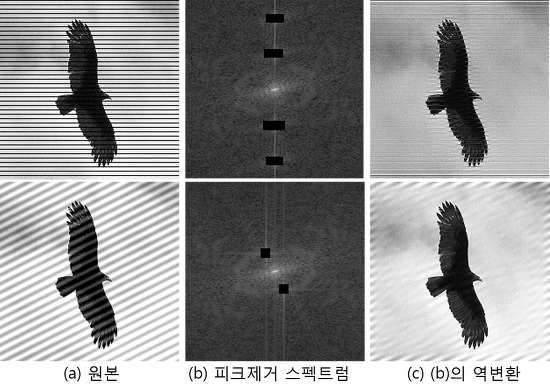
- 스펙트럼의 피크 영역을 지운 후 푸리에 역변환(Inverse Fourier Transform)을 하면 다음과 같은 결과가 나타날 수 있다.
-
푸리에 변환의 성질
1) 선형성
- 위의 식과 같이 \((f_1(x, y))\)와 \((f_2(x, y))\)의 덧셈 조합으로 표현될 경우, 이 함수의 푸리에 변환은 두 함수를 따로 푸리에 변환하여 더한 것과 같다.
- 이러한 선형성은 입력 신호 f(x, y)를 여러 개의 간단한 형태의 함수 조합으로 분리되고, 각 함수를 이산 푸리에 변환한 후 다시 더해줌으로써 원본 함수의 이산 푸리에 변환을 생성할 수 있다.2) 이동변환
- 영상의 이동변환이 이산 푸리에 결과에서 푸리에 스펙트럼은 동일하고, 위상에만 영향을 준다는 것을 의미한다.
- 이와 반대로 주파수 공간에서의 이동변환이 원본 영상의 값에 미치는 영향은 아래와 같다.
3) 크기변환
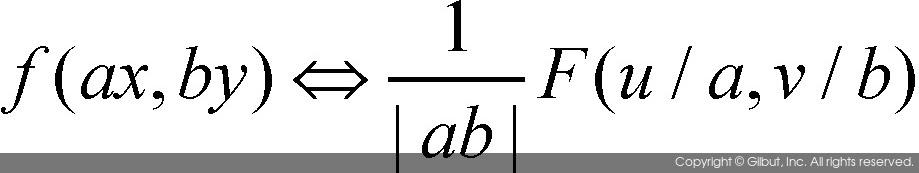
- 영상을 가로 방향으로 a배, 세로 방향으로 b배 크기만큼 확대한 영상을 푸리에 변환하면 위와 같다.4) 회전변환
- 영상을 \(\Theta_0\) 크기만큼 회전한 후 푸리에 변환을 하면, 푸리에 변환된 함수도 같은 크기만큼 회전이 됨을 의미한다.
10.1.3. 개선된 푸리에 변환
- 위에서 구해진 푸리에 변환은 4중 for문 루프를 사용하고 있으며, 다수의 곱셈 연산을 호출하기 때문에 연산 속도가 매우 느리다.
- 이를 해결하기 위해 이산 푸리에 변환식을 행과 열 단위로 분리하여 각각의 푸리에 변환을 구한다.
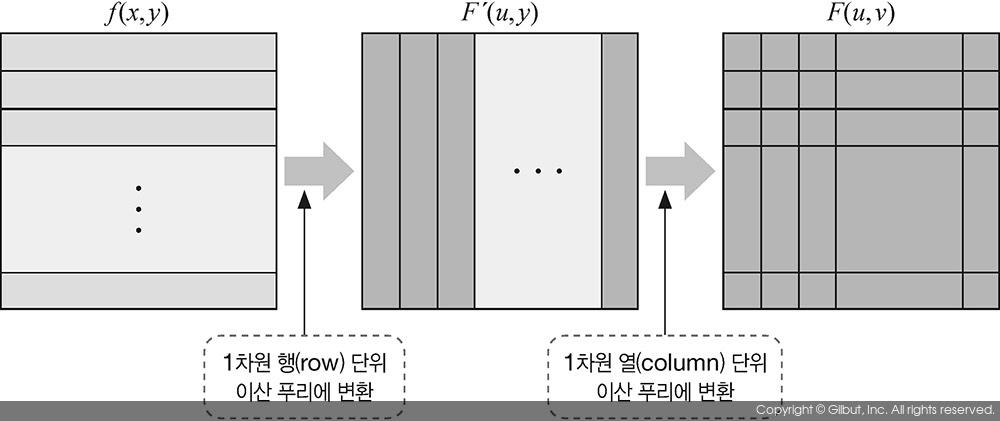
10.1.4. 고속 푸리에 변환
- 행과 열 단위로 분리하여 푸리에 변환을 구하여 속도를 향상시켰지만, 아직까지 적합하지 않다.
- DFT 계산식에서 반복되는 연산을 최소화함으로써 푸리에 변환 계산 속도를 향상시키는 알고리즘을 고속 푸리에 변환(Fast Fourier Transform)이라고 한다.
- 고속 푸리에 변환 알고리즘은 원래 1차원 데이터에 대하여 정의된 알고리즘이며, 입력 데이터의 개수가 2의 승수로 이루어질 때에만 적용이 가능하다.
- 고속 푸리에 변환은 짝수 번째 데이터와 홀수 번째 데이터를 따로 분리하여 계산하는 방식이다.
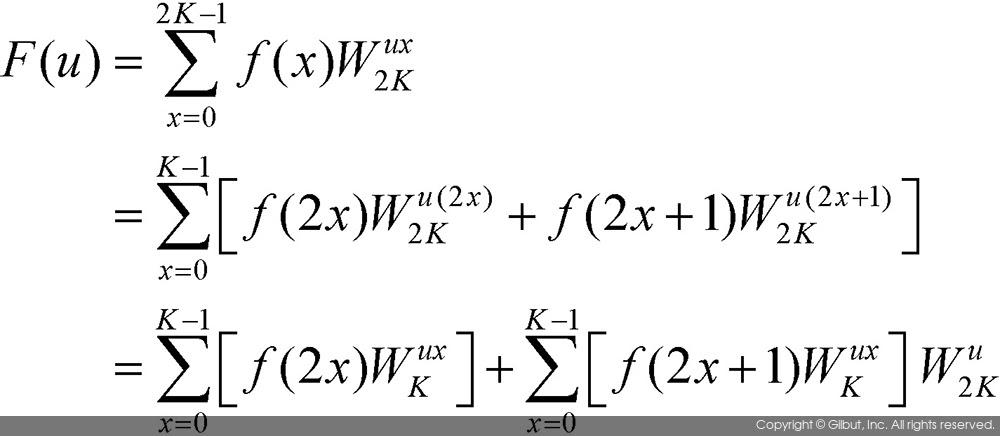
- 고속 푸리에 변환의 핵심 이론은 N=2K개의 데이터를 이산 푸리에 변환을 할 경우, 짝수 번째 데이터들과 홀수 번째 데이터들을 이용하여 K개의 푸리에 변환 결과를 얻으면, 나머지 K개의 푸리에 변환 결과는 복잡한 연산없이 쉽게 구할 수 있다.
- 이러한 연산 방법을 버터플라이(butterfly) 방법이라고 부른다.
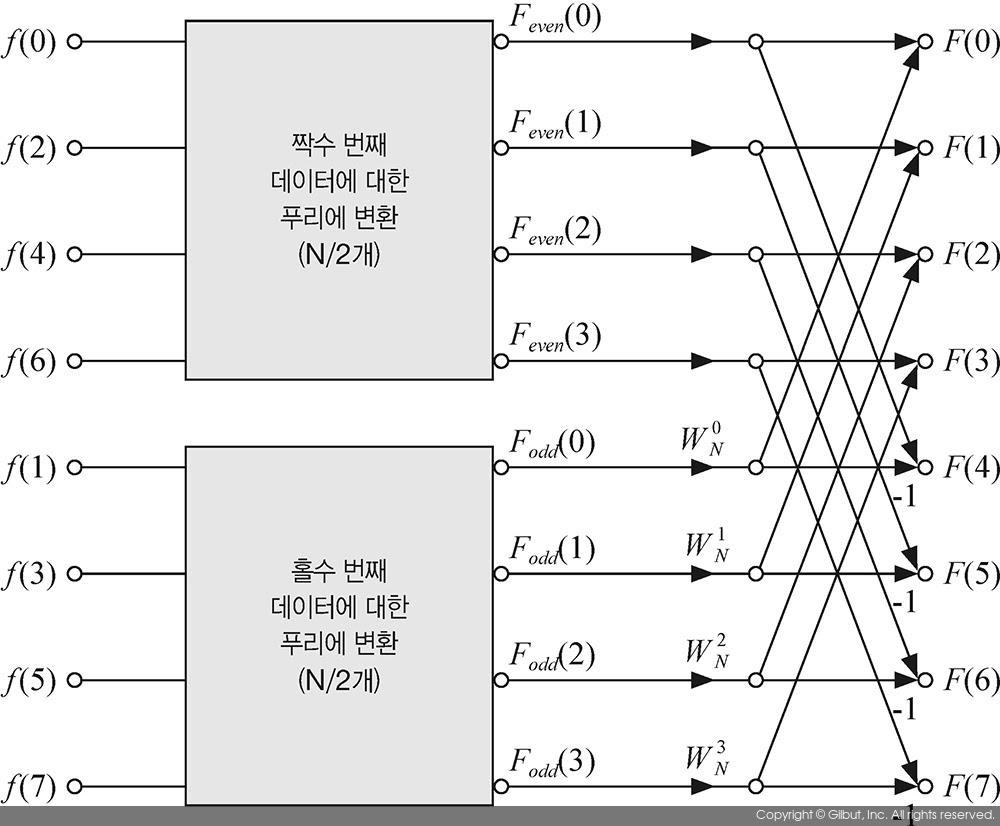
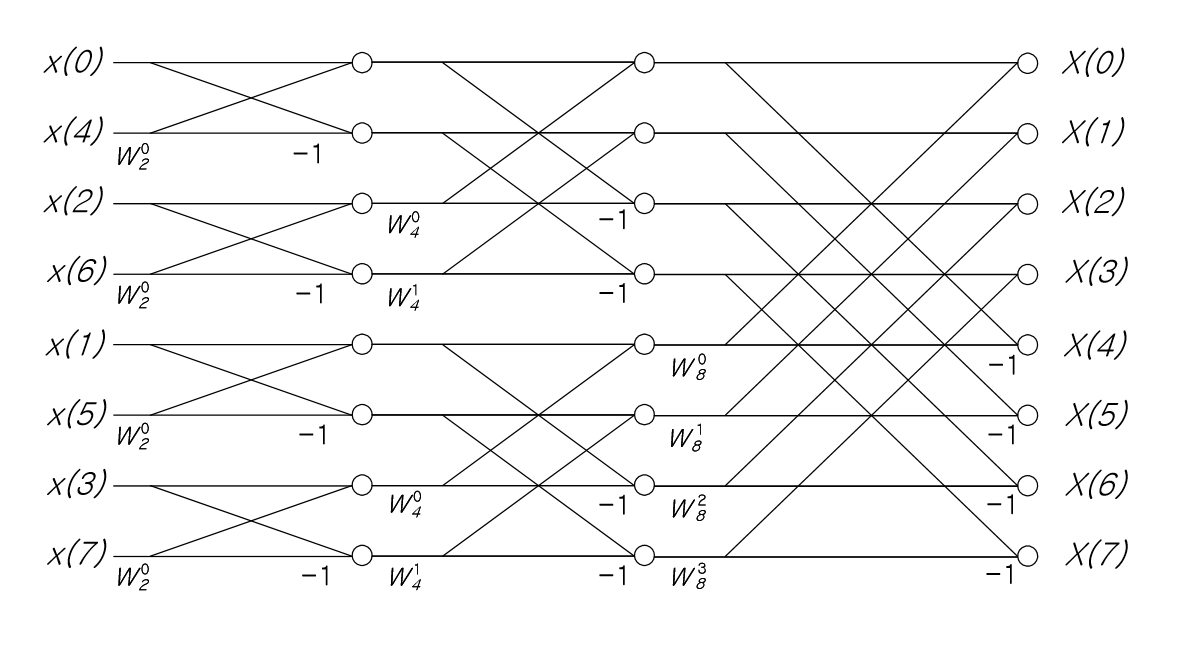
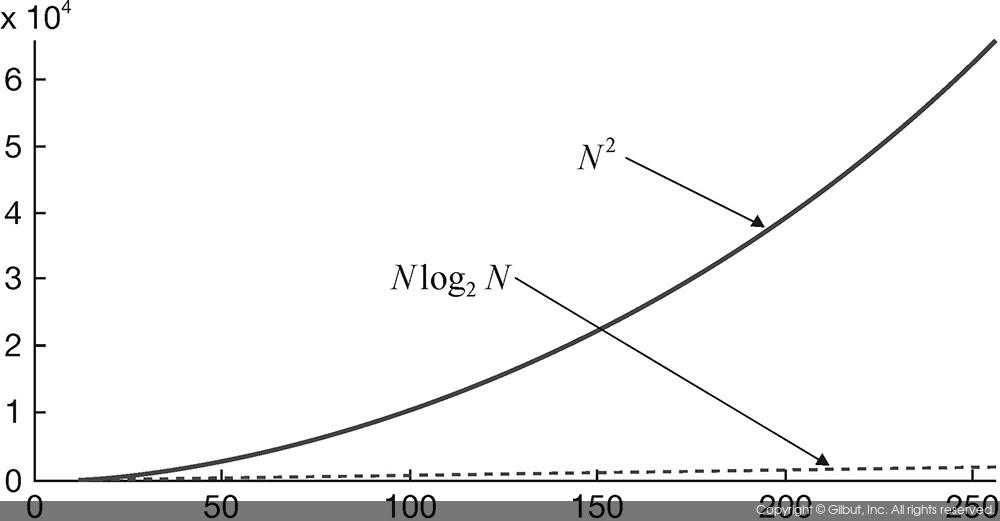
- 일반 이산 푸리에 변환(DFT)와 비교했을 떄, 고속 푸리에 변환(FFT)의 연산량이 훨씬 적다는 것을 알 수 있다.
10.1.5. 주파수 공간에서의 필터링
- 일반적으로 영상에서 픽셀의 값이 급격하게 변화하는 부분을 고주파(high frequency) 성분이 강하다고 하며, 상대적으로 픽셀값이 일정하거나 완만하게 변화하는 부분은 저주파(low frequency) 성분이 강하다고 한다.
- 체크 무늬 셔츠 사진 -> 고주파 성분이 강함.
- 맑은 하늘 사진 -> 저주파 성분이 강함.
- 주파수 공간에서 정의된 함수 F(u, v)에서 F(0, 0)에 가까운 위치의 값들을 저주파 성분이라고 하며, F(0, 0)에서 멀리 떨어진 위치의 값들을 고주파 성분이라고 한다.
- 주의해야 할 점은 영상과 같이 실수로 이루어진 함수를 푸리에 변환하면 입력 영상의 크기가 절반에 해당하는 신호가 대칭적으로 나타나기 때문에, 가장 강한 고주파 성분은 F(M/2, N/2) 위치가 된다.
- 주파수 공간에서의 필터링 방법은 다음과 같다.

-
주파수 공간에서의 필터링은 다음과 같은 수식이다.
- F(u, v)는 입력 영상이 이산 푸리에 변환되어 생성된 함수이다.
- H(u, v)는 필터 함수이다.
- G(u, v)는 필터링된 결과함수이다.
- 즉, 주파수 공간에서의 필터링은 함수의 특정 좌표의 값을 같은 좌표에서의 필터의 값과 곱하여 결과를 생성한다.
- 저역 통과 필터(lowpass filter)
- 저주파 성분만을 통과시키는 함수
- 저주파에 해당하는 위치의 함숫값만을 남기고 나머지 부분의 함숫값은 모두 0으로 만든다.
- 고역 통과 필터(highpass filter)
- 고주파 성분만을 통과시키는 함수
- 고주파에 해당하는 위치의 함숫값만을 남기고 나머지 부분의 함숫값을 모두 0으로 만든다.
- 저역 통과 필터와 고역 통과 필터의 수식
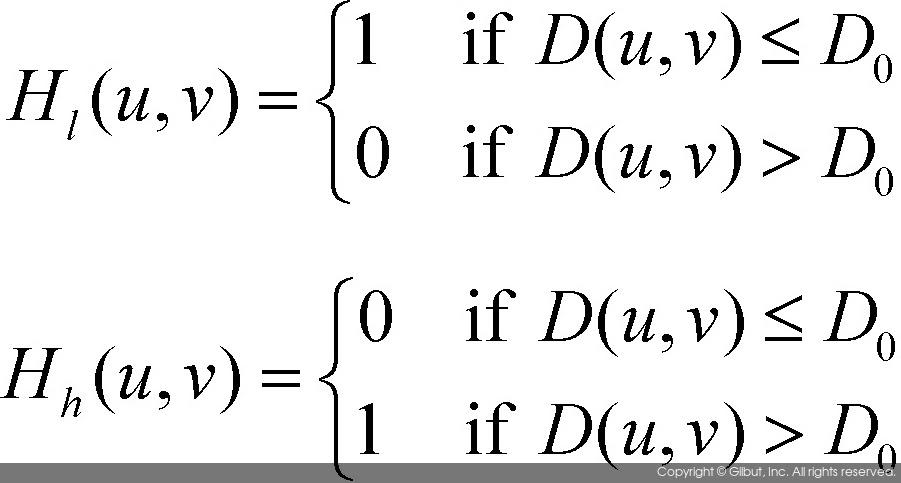
- \(D_0\)값은 임의의 양수값으로 차단 주파수(cutoff frequency)라고 부르며, 이는 저역 통과 필터 및 고역 통과 필터에서 걸러낼 주파수 성분의 양을 결정하는 값이다.
- 저역 통과 필터는 \(H_1(u, v)\)로, \(D_0\)값이 작아지면 적은 양의 저주파 성분만을 통과시키며, \(D_0\)값이 커지면 많은 양의 저주파 성분을 통과시킨다.
- 저역 통과 필터와 고역 통과 필터 결과 영상
- (a)는 원본 영상, (b)와 (c)는 차단 주파수가 각각 16, 32인 저역 통과 핕터링 결과 영상
- (d)와 (e)는 차단 주파수가 각각 16, 32인 고역 통과 필터링 결과 영상
- 가우시안 통과 필터
- 위에서 구한 차단 주파수는 임의로 설정했다면, 이번에는 가우시안 분포를 따라 설정해주는 가우시안 통과 필터이다.
- 가우시안 저역 통과 필터
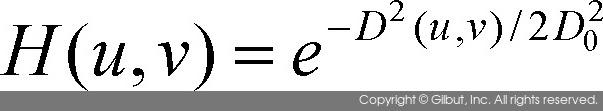
- 가우시안 고역 통과 필터
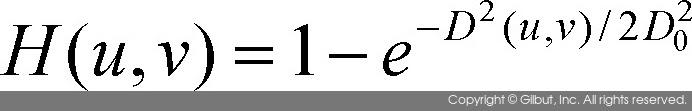
10.2. 변환영역 처리 실습
10.2.1. 공간 주파수의 이해
- 공간 주파수는 밝기의 변화 정도에 따라서 고주파 영역과 저주파 영역으로 분류한다.
- 저주파 공간 영역
- 화소 밝기가 거의 변화가 없거나 점진적으로 변화하는 것
- 영상에서 배경 부분이나 객체의 내부에 많이 있음
- 고주파 공간 영역
- 화소 밝기가 급변하는 것
- 경계부분이나 객체의 모서리 부분

- 경계 부분에 많은 고주파 성분을 제거하면, 경계가 흐려지는 영상을 얻을 수 있다.
- 경계 부분에 고주파 성분만을 취하면, 경계나 모서리만 포함하는 엣지 영상을 얻을 수 있다.
- 공간 영역상에서 저주파 성분과 고주파 성분이 혼합되어 있기 때문에 영역을 분리해서 선별적 처리가 어렵다. 따라서 변환영역에 대한 처리가 필요하다.
- 변환 영역 처리 과정
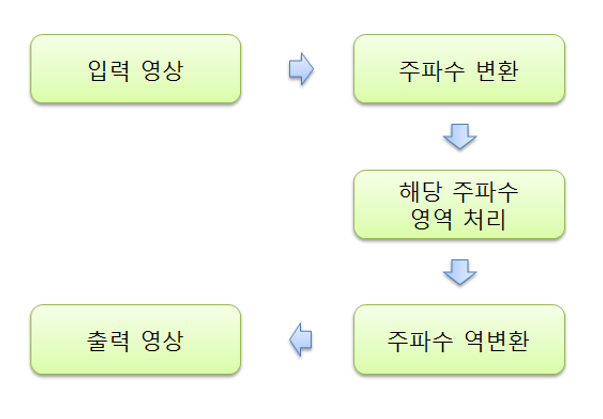
10.2.2. 이산 푸리에 변환
- 2차원 이산 푸리에 변환
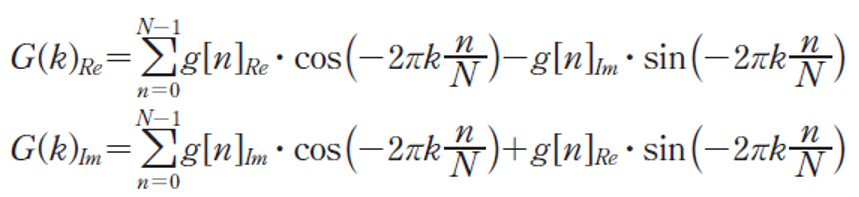
- 2차원 이산 푸리에 역변환
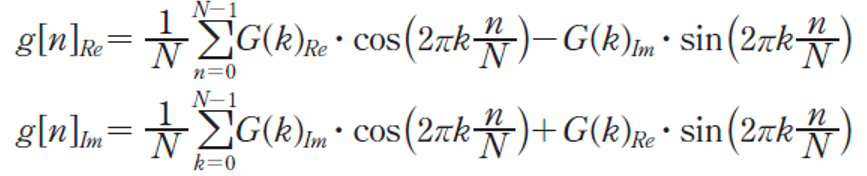
- 복소수의 실수부와 허수부를 벡터로 간주하여 벡터의 크기를 계산(주파수 스펙트럼)
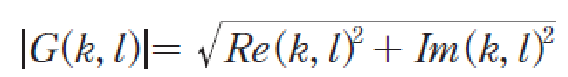
- 복소수의 실수부와 허수부의 기울기를 계산(주파수 위상)
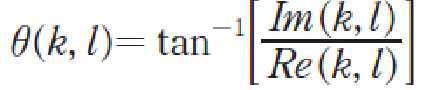
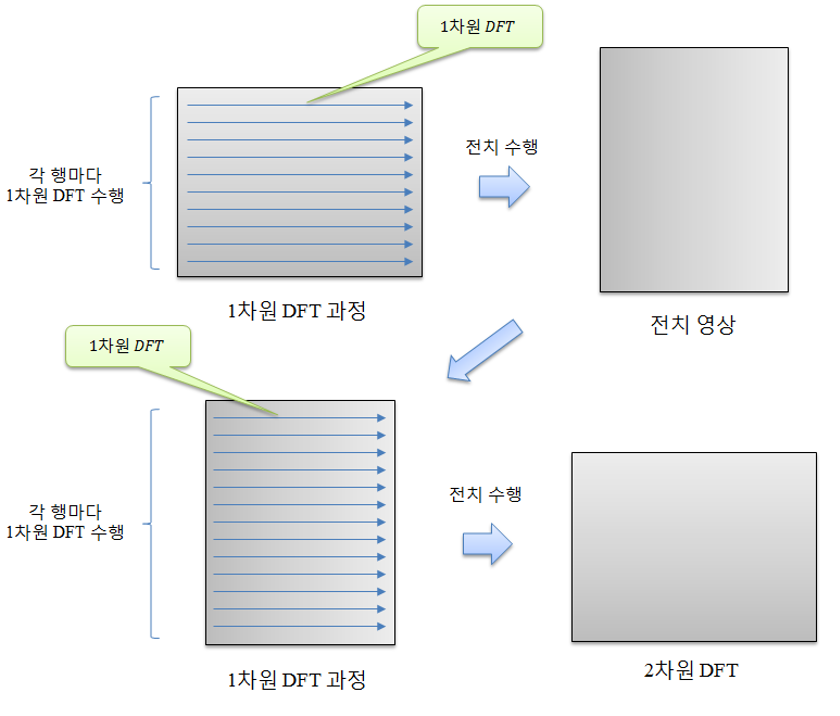
- 2차원 이산 푸리에 변환 수행 방법
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void log_mag(Mat complex_mat, Mat& dst)
{
Mat planes[2];
split(complex_mat, planes); // 2채널 복소 행렬 분리(실수부, 허수부로)
magnitude(planes[0], planes[1], dst); // 크기 계산
log(dst+1, dst); // magnitude에 1을 더해서 로그로 scale(10, 100, 1000 등의 값이 나올 수 있음 -> 정규화가 필요)
normalize(dst, dst, 0, 255, CV_MINMAX); // 정규화 수행(화면에 뿌려주기 위해서 0과 255사이값)
dst.convertTo(dst, CV_8U);
}
void shuffling(Mat mag_img, Mat& dst)
{
int cx = mag_img.rows / 2;
int cy = mag_img.cols / 2;
// 각 사분면 관심영역 지정
Rect q1(cx, 0, cx, cy); // 1사분면 사각형
Rect q2(0, 0, cx, cy); // 2사분면 사각형
Rect q3(0, cy, cx, cy); // 3사분면 사각형
Rect q4(cx, cy, cx, cy); // 4사분면 사각형
dst = Mat(mag_img.size(), mag_img.type());
mag_img(q1).copyTo(dst(q3));
mag_img(q3).copyTo(dst(q1));
mag_img(q2).copyTo(dst(q4));
mag_img(q4).copyTo(dst(q2));
}
// 1차원 신호의 이산 푸리에 변환 수행
Mat DFT_1D(Mat one_row, int dir)
{
int N = (int)one_row.total();
Mat dst(one_row.size(), CV_32FC2);
for (int k = 0; k < N; k++) {
Vec2f complex(0, 0);
for (int n = 0; n < N; n++)
{
float theta = (float)(dir * -2 * CV_PI * k * n / N); // 기저함수의 각도 계산
Vec2f value = one_row.at<Vec2f>(n);
complex[0] += (value[0] * cos(theta) - value[1] * sin(theta));
complex[1] += (value[1] * cos(theta) + value[0] * sin(theta));
}
dst.at<Vec2f>(k) = complex;
}
// -1이면 역변환, n으로 나눠줘야 함
if (dir == -1) dst /= N;
return dst;
}
void DFT_2D(Mat complex_img, Mat& dst, int dir)
{
complex_img.convertTo(complex_img, CV_32F);
Mat tmp(complex_img.size(), CV_32FC2, Vec2f(0, 0));
tmp.copyTo(dst);
for (int i = 0; i < complex_img.rows; i++) {
Mat one_row = complex_img.row(i);
Mat dft_row = DFT_1D(one_row, dir);
dft_row.copyTo(tmp.row(i));
}
transpose(tmp, tmp);
for (int i = 0; i < tmp.rows; i++) {
Mat one_row = tmp.row(i);
Mat dft_row = DFT_1D(tmp.row(i), dir);
dft_row.copyTo(dst.row(i));
}
transpose(dst, dst);
}
int main()
{
Mat image = imread("../image/dft_test1.jpg", 0);
CV_Assert(image.data);
Mat complex_img, dft_coef, dft_img, idft_coef, shuffling_img, idft_img[2];
Mat tmp[] = { image, Mat::zeros(image.size(), CV_8U) }; // 실수부를 영상, 허수부를 0값으로
merge(tmp, 2, complex_img);
DFT_2D(complex_img, dft_coef, 1); // 푸리에 정변환
log_mag(dft_coef, dft_img); // 로그 정규화
shuffling(dft_img, shuffling_img);
DFT_2D(dft_coef, idft_coef, -1); // 푸리에 역변환
split(idft_coef, idft_img);
idft_img[0].convertTo(idft_img[0], CV_8U);
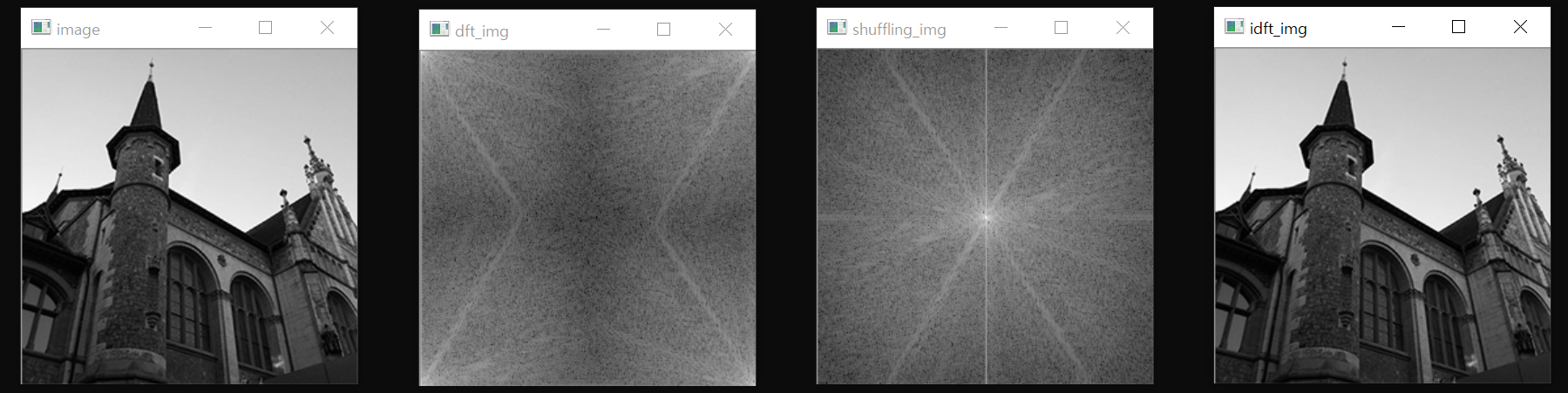
imshow("image", image);
imshow("dft_img", dft_img);
imshow("shuffling_img", shuffling_img);
imshow("idft_img", idft_img[0]);
waitKey();
return 0;
}
10.2.2.1. 실습 1
shuffling_img 영상의 원점에 반지름 20인 검은색 원(색=0)을 그린 것과 같은 효과를 내도록 푸리에 변환 영상을 처리 후 푸리에 역변환 결과를 확인하시오.

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void log_mag(Mat complex_mat, Mat& dst)
{
Mat planes[2];
split(complex_mat, planes); // 2채널 복소 행렬 분리(실수부, 허수부로)
magnitude(planes[0], planes[1], dst); // 크기 계산
log(dst + 1, dst); // magnitude에 1을 더해서 로그로 scale(10, 100, 1000 등의 값이 나올 수 있음 -> 정규화가 필요)
normalize(dst, dst, 0, 255, CV_MINMAX); // 정규화 수행(화면에 뿌려주기 위해서 0과 255사이값)
dst.convertTo(dst, CV_8U);
}
void shuffling(Mat mag_img, Mat& dst)
{
int cx = mag_img.rows / 2;
int cy = mag_img.cols / 2;
// 각 사분면 관심영역 지정
Rect q1(cx, 0, cx, cy); // 1사분면 사각형
Rect q2(0, 0, cx, cy); // 2사분면 사각형
Rect q3(0, cy, cx, cy); // 3사분면 사각형
Rect q4(cx, cy, cx, cy); // 4사분면 사각형
dst = Mat(mag_img.size(), mag_img.type());
mag_img(q1).copyTo(dst(q3));
mag_img(q3).copyTo(dst(q1));
mag_img(q2).copyTo(dst(q4));
mag_img(q4).copyTo(dst(q2));
}
// 1차원 신호의 이산 푸리에 변환 수행
Mat DFT_1D(Mat one_row, int dir)
{
int N = (int)one_row.total();
Mat dst(one_row.size(), CV_32FC2);
for (int k = 0; k < N; k++) {
Vec2f complex(0, 0);
for (int n = 0; n < N; n++)
{
float theta = (float)(dir * -2 * CV_PI * k * n / N); // 기저함수의 각도 계산
Vec2f value = one_row.at<Vec2f>(n);
complex[0] += (value[0] * cos(theta) - value[1] * sin(theta));
complex[1] += (value[1] * cos(theta) + value[0] * sin(theta));
}
dst.at<Vec2f>(k) = complex;
}
// -1이면 역변환, n으로 나눠줘야 함
if (dir == -1) dst /= N;
return dst;
}
void DFT_2D(Mat complex_img, Mat& dst, int dir)
{
complex_img.convertTo(complex_img, CV_32F);
Mat tmp(complex_img.size(), CV_32FC2, Vec2f(0, 0));
tmp.copyTo(dst);
for (int i = 0; i < complex_img.rows; i++) {
Mat one_row = complex_img.row(i);
Mat dft_row = DFT_1D(one_row, dir);
dft_row.copyTo(tmp.row(i));
}
transpose(tmp, tmp);
for (int i = 0; i < tmp.rows; i++) {
Mat one_row = tmp.row(i);
Mat dft_row = DFT_1D(tmp.row(i), dir);
dft_row.copyTo(dst.row(i));
}
transpose(dst, dst);
}
int main()
{
Mat image = imread("../image/dft_test1.jpg", 0);
CV_Assert(image.data);
Mat complex_img, dft_coef, dft_img, idft_coef, shuffling_img, idft_img[2];
Mat tmp[] = { image, Mat::zeros(image.size(), CV_8U) }; // 실수부를 영상, 허수부를 0값으로
merge(tmp, 2, complex_img);
DFT_2D(complex_img, dft_coef, 1); // 푸리에 정변환
Mat planes[2];
split(dft_coef, planes);
circle(planes[0], Point(0, 0), 20, Scalar(0), -1);
circle(planes[0], Point(dft_coef.cols, 0), 20, Scalar(0), -1);
circle(planes[0], Point(0, dft_coef.rows), 20, Scalar(0), -1);
circle(planes[0], Point(dft_coef.cols, dft_coef.rows), 20, Scalar(0), -1);
circle(planes[1], Point(0, 0), 20, Scalar(0), -1);
circle(planes[1], Point(dft_coef.cols, 0), 20, Scalar(0), -1);
circle(planes[1], Point(0, dft_coef.rows), 20, Scalar(0), -1);
circle(planes[1], Point(dft_coef.cols, dft_coef.rows), 20, Scalar(0), -1);
merge(planes, 2, dft_coef);
log_mag(dft_coef, dft_img); // 로그 정규화
shuffling(dft_img, shuffling_img);
DFT_2D(dft_coef, idft_coef, -1); // 푸리에 역변환
split(idft_coef, idft_img);
idft_img[0].convertTo(idft_img[0], CV_8U);
imshow("image", image);
imshow("dft_img", dft_img);
imshow("shuffling_img", shuffling_img);
imshow("idft_img", idft_img[0]);
waitKey();
return 0;
}
10.2.2.2. 실습 2
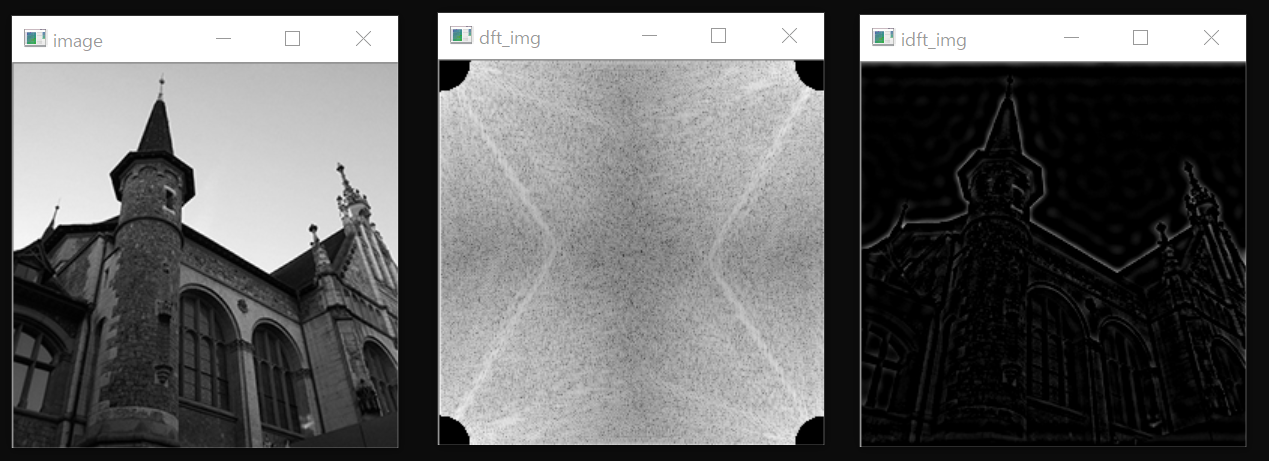
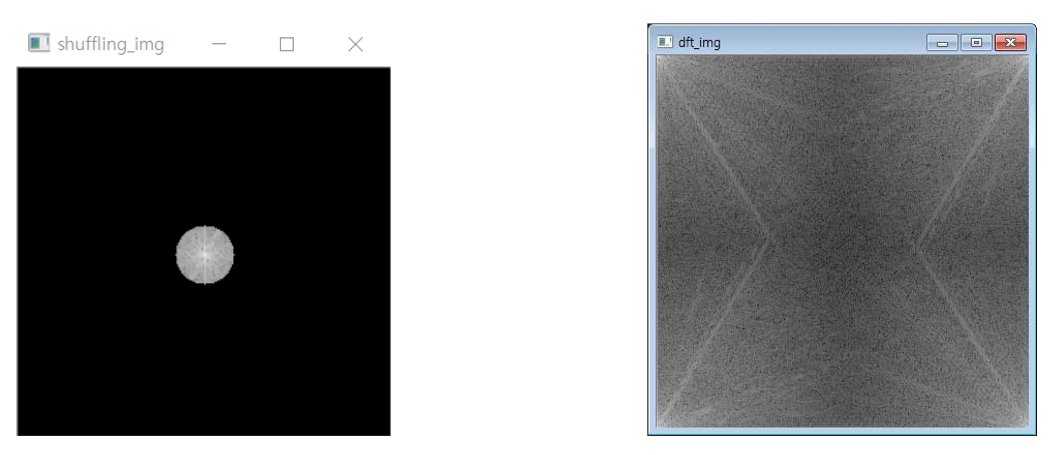
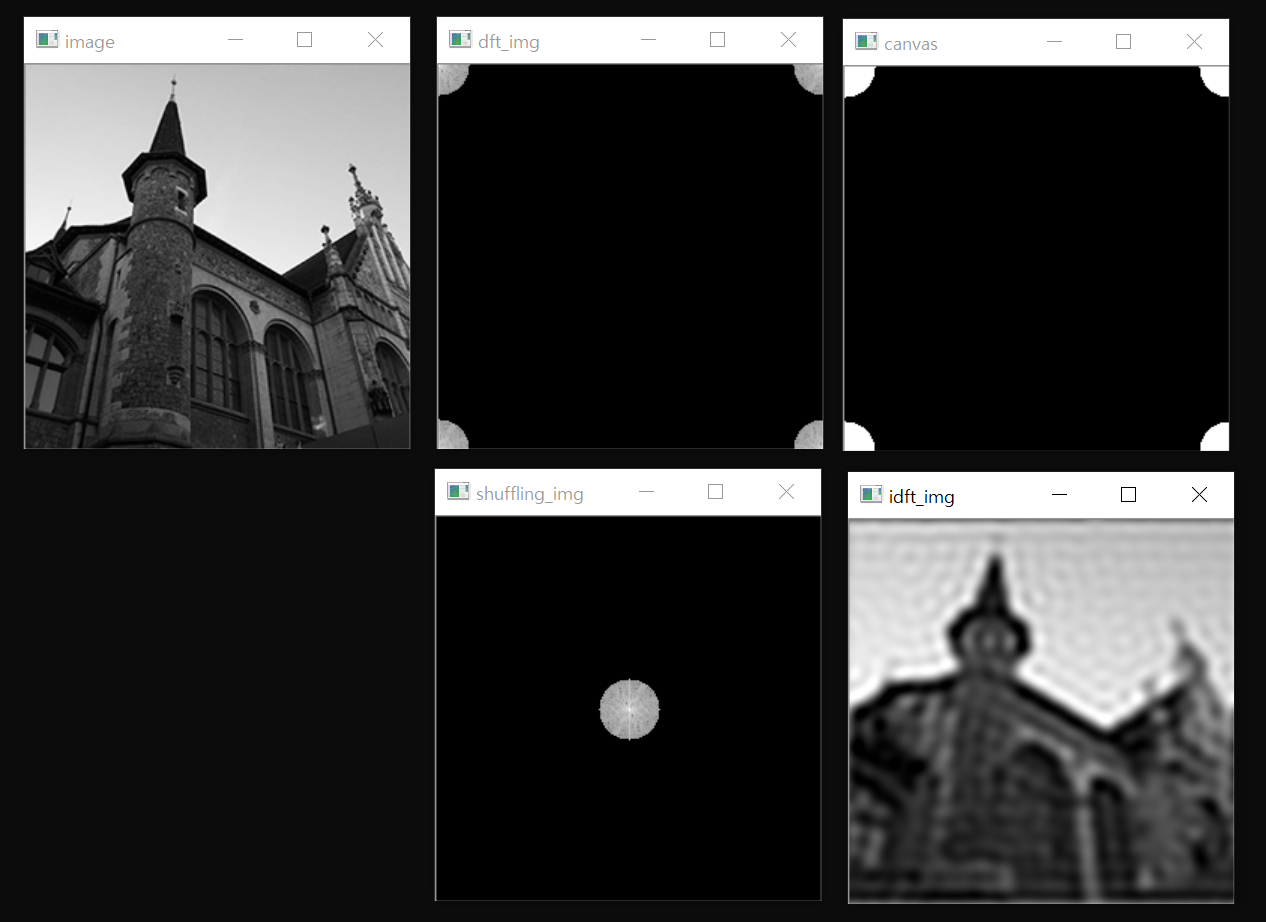
shuffling_img 영상의 원점에 반지름 20인 검은색 원을 그린 후 그 외부를 0으로 만든 효과를 내도록 푸리에 변환 영상을 처리 후 푸리에 역변환 결과를 확인하시오.
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void log_mag(Mat complex_mat, Mat& dst)
{
Mat planes[2];
split(complex_mat, planes); // 2채널 복소 행렬 분리(실수부, 허수부로)
magnitude(planes[0], planes[1], dst); // 크기 계산
log(dst + 1, dst); // magnitude에 1을 더해서 로그로 scale(10, 100, 1000 등의 값이 나올 수 있음 -> 정규화가 필요)
normalize(dst, dst, 0, 255, CV_MINMAX); // 정규화 수행(화면에 뿌려주기 위해서 0과 255사이값)
dst.convertTo(dst, CV_8U);
}
void shuffling(Mat mag_img, Mat& dst)
{
int cx = mag_img.rows / 2;
int cy = mag_img.cols / 2;
// 각 사분면 관심영역 지정
Rect q1(cx, 0, cx, cy); // 1사분면 사각형
Rect q2(0, 0, cx, cy); // 2사분면 사각형
Rect q3(0, cy, cx, cy); // 3사분면 사각형
Rect q4(cx, cy, cx, cy); // 4사분면 사각형
dst = Mat(mag_img.size(), mag_img.type());
mag_img(q1).copyTo(dst(q3));
mag_img(q3).copyTo(dst(q1));
mag_img(q2).copyTo(dst(q4));
mag_img(q4).copyTo(dst(q2));
}
// 1차원 신호의 이산 푸리에 변환 수행
Mat DFT_1D(Mat one_row, int dir)
{
int N = (int)one_row.total();
Mat dst(one_row.size(), CV_32FC2);
for (int k = 0; k < N; k++) {
Vec2f complex(0, 0);
for (int n = 0; n < N; n++)
{
float theta = (float)(dir * -2 * CV_PI * k * n / N); // 기저함수의 각도 계산
Vec2f value = one_row.at<Vec2f>(n);
complex[0] += (value[0] * cos(theta) - value[1] * sin(theta));
complex[1] += (value[1] * cos(theta) + value[0] * sin(theta));
}
dst.at<Vec2f>(k) = complex;
}
// -1이면 역변환, n으로 나눠줘야 함
if (dir == -1) dst /= N;
return dst;
}
void DFT_2D(Mat complex_img, Mat& dst, int dir)
{
complex_img.convertTo(complex_img, CV_32F);
Mat tmp(complex_img.size(), CV_32FC2, Vec2f(0, 0));
tmp.copyTo(dst);
for (int i = 0; i < complex_img.rows; i++) {
Mat one_row = complex_img.row(i);
Mat dft_row = DFT_1D(one_row, dir);
dft_row.copyTo(tmp.row(i));
}
transpose(tmp, tmp);
for (int i = 0; i < tmp.rows; i++) {
Mat one_row = tmp.row(i);
Mat dft_row = DFT_1D(tmp.row(i), dir);
dft_row.copyTo(dst.row(i));
}
transpose(dst, dst);
}
int main()
{
Mat image = imread("../image/dft_test1.jpg", 0);
CV_Assert(image.data);
Mat complex_img, dft_coef, dft_img, idft_coef, shuffling_img, idft_img[2];
Mat tmp[] = { image, Mat::zeros(image.size(), CV_8U) }; // 실수부를 영상, 허수부를 0값으로
merge(tmp, 2, complex_img);
DFT_2D(complex_img, dft_coef, 1); // 푸리에 정변환
Mat planes[2];
split(dft_coef, planes);
Mat canvas(dft_coef.rows, dft_coef.cols, CV_8U);
canvas = 0;
circle(canvas, Point(0, 0), 20, Scalar(255), -1);
circle(canvas, Point(dft_coef.cols, 0), 20, Scalar(255), -1);
circle(canvas, Point(0, dft_coef.rows), 20, Scalar(255), -1);
circle(canvas, Point(dft_coef.cols, dft_coef.rows), 20, Scalar(255), -1);
imshow("canvas", canvas);
for (int i = 0; i < dft_coef.rows; i++) {
for (int j = 0; j < dft_coef.cols; j++) {
if (canvas.at<uchar>(i, j) == 0) {
planes[0].at<float>(i, j) = 0;
planes[1].at<float>(i, j) = 0;
}
}
}
// vector<Mat> planesVec(2);
// planesVec[0] = planes[0];
// planesVec[1] = planes[1];
// merge(planesVec, dft_coef);
merge(planes, 2, dft_coef);
log_mag(dft_coef, dft_img); // 로그 정규화
shuffling(dft_img, shuffling_img);
DFT_2D(dft_coef, idft_coef, -1); // 푸리에 역변환
split(idft_coef, idft_img);
idft_img[0].convertTo(idft_img[0], CV_8U);
imshow("image", image);
imshow("dft_img", dft_img);
imshow("shuffling_img", shuffling_img);
imshow("idft_img", idft_img[0]);
waitKey();
return 0;
}
10.2.3. 고속 푸리에 변환
- 삼각함수의 주기성을 이용해 작은 단위로 분리하여, 반복적으로 수행하고 합해져서 효율성이 높아졌다.
- 푸리에 변환의 수식을 짝수부와 홀수부로 분리한다.
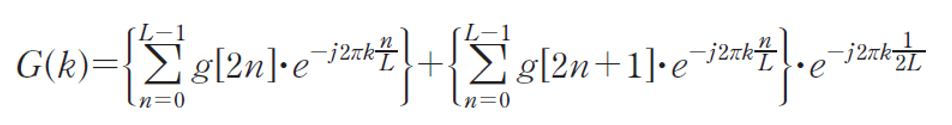
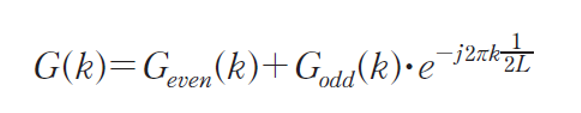
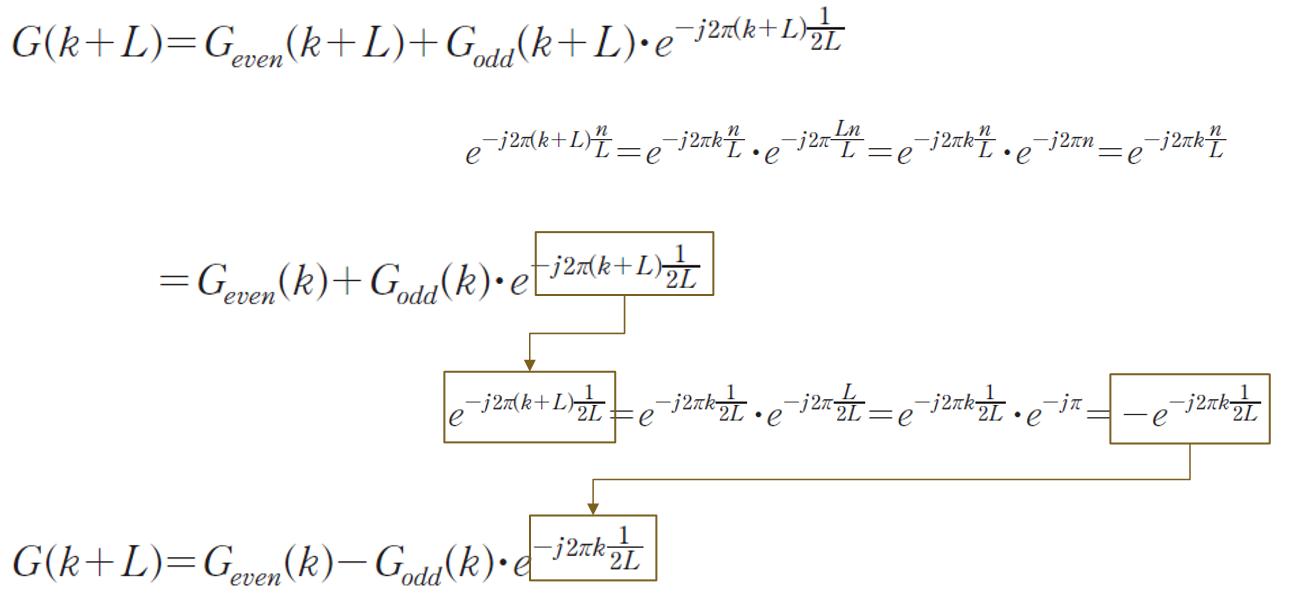
- 버터플라이 방법을 이용한다.
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void log_mag(Mat complex_mat, Mat& dst)
{
Mat planes[2];
split(complex_mat, planes);
magnitude(planes[0], planes[1], dst);
log(dst + 1, dst);
normalize(dst, dst, 0, 255, CV_MINMAX);
dst.convertTo(dst, CV_8U);
}
void shuffling(Mat mag_img, Mat& dst)
{
int cx = mag_img.cols / 2;
int cy = mag_img.rows / 2;
Rect q1(cx, 0, cx, cy); // 1사분면 사각형
Rect q2(0, 0, cx, cy); // 2사분면 사각형
Rect q3(0, cy, cx, cy); // 3사분면 사각형
Rect q4(cx, cy, cx, cy); // 4사분면 사각형
dst = Mat(mag_img.size(), mag_img.type());
mag_img(q1).copyTo(dst(q3));
mag_img(q3).copyTo(dst(q1));
mag_img(q2).copyTo(dst(q4));
mag_img(q4).copyTo(dst(q2));
}
Mat scramble(Mat signal)
{
Mat dst = signal.clone();
for (int i = 0, j = 0; i < dst.cols - 1; i++)
{
if (i > j) {
swap(dst.at<Vec2f>(i), dst.at<Vec2f>(j));
}
int m = dst.cols >> 1;
while ((j >= m) && (m >= 2))
{
j -= m;
m >>= 1;
}
j += m;
}
return dst;
}
Mat zeropadding(Mat img)
{
int m = 1 << (int)ceil(log2(img.rows));
int n = 1 << (int)ceil(log2(img.cols));
Mat dst(m, n, img.type(), Scalar(0));
Rect rect(Point(0, 0), img.size());
img.copyTo(dst(rect));
dst.convertTo(dst, CV_32F);
return dst;
}
void butterfly(Mat& dst, int dir)
{
int length = dst.cols;
int pair = 1;
for (int k = 0; k < ceil(log2(length)); k++)
{
int half_pair = pair;
pair <<= 1;
float theta = dir * (-2.0 * CV_PI / pair);
float wpr = -2.0 * sin(0.5 * theta) * sin(0.5 * theta);
float wpi = sin(theta);
float wre = 1.0;
float wim = 0.0;
for (int m = 0; m < half_pair; m++) {
for (int even = m; even < length; even += pair)
{
int odd = even + half_pair;
Vec2f G_even = dst.at<Vec2f>(even);
Vec2f G_odd = dst.at<Vec2f>(odd);
Vec2f G_odd_W(0, 0);
G_odd_W[0] = G_odd[0] * wre - G_odd[1] * wim;
G_odd_W[1] = G_odd[1] * wre + G_odd[0] * wim;
dst.at<Vec2f>(even) = G_even + G_odd_W;
dst.at<Vec2f>(odd) = G_even - G_odd_W;
}
float tmp = wre;
wre += tmp * wpr - wim * wpi;
wim += wim * wpr + tmp * wpi;
}
}
if (dir == -1) dst /= dst.cols;
}
void FFT_2D(Mat complex_img, Mat& dst, int dir)
{
dst = Mat(complex_img.size(), complex_img.type());
for (int i = 0; i < complex_img.rows; i++)
{
Mat scr_sn = scramble(complex_img.row(i));
butterfly(scr_sn, dir);
scr_sn.copyTo(dst.row(i));
}
transpose(dst, dst);
for (int i = 0; i < dst.rows; i++) {
Mat scr_sn = scramble(dst.row(i));
butterfly(scr_sn, dir);
scr_sn.copyTo(dst.row(i));
}
transpose(dst, dst);
}
int main()
{
Mat complex_img, idft_img, img_tmp[2];
Mat dft_coef1, dft_img1, shuffling_img1;
Mat dft_coef2, dft_img2, shuffling_img2;
Mat image = imread("../image/fft_test.jpg", 0);
CV_Assert(image.data);
Mat pad_img = zeropadding(image);
Mat tmp[] = { pad_img, Mat::zeros(pad_img.size(), pad_img.type()) };
merge(tmp, 2, complex_img);
FFT_2D(complex_img, dft_coef1, 1);
log_mag(dft_coef1, dft_img1);
shuffling(dft_img1, shuffling_img1);
dft(complex_img, dft_coef2);
log_mag(dft_coef2, dft_img2);
shuffling(dft_img2, shuffling_img2);
dft(dft_coef2, idft_img, DFT_INVERSE + DFT_SCALE);
split(idft_img, img_tmp);
cout << img_tmp[0](Rect(100, 100, 10, 10)) << endl;
img_tmp[0].convertTo(img_tmp[0], CV_8U);
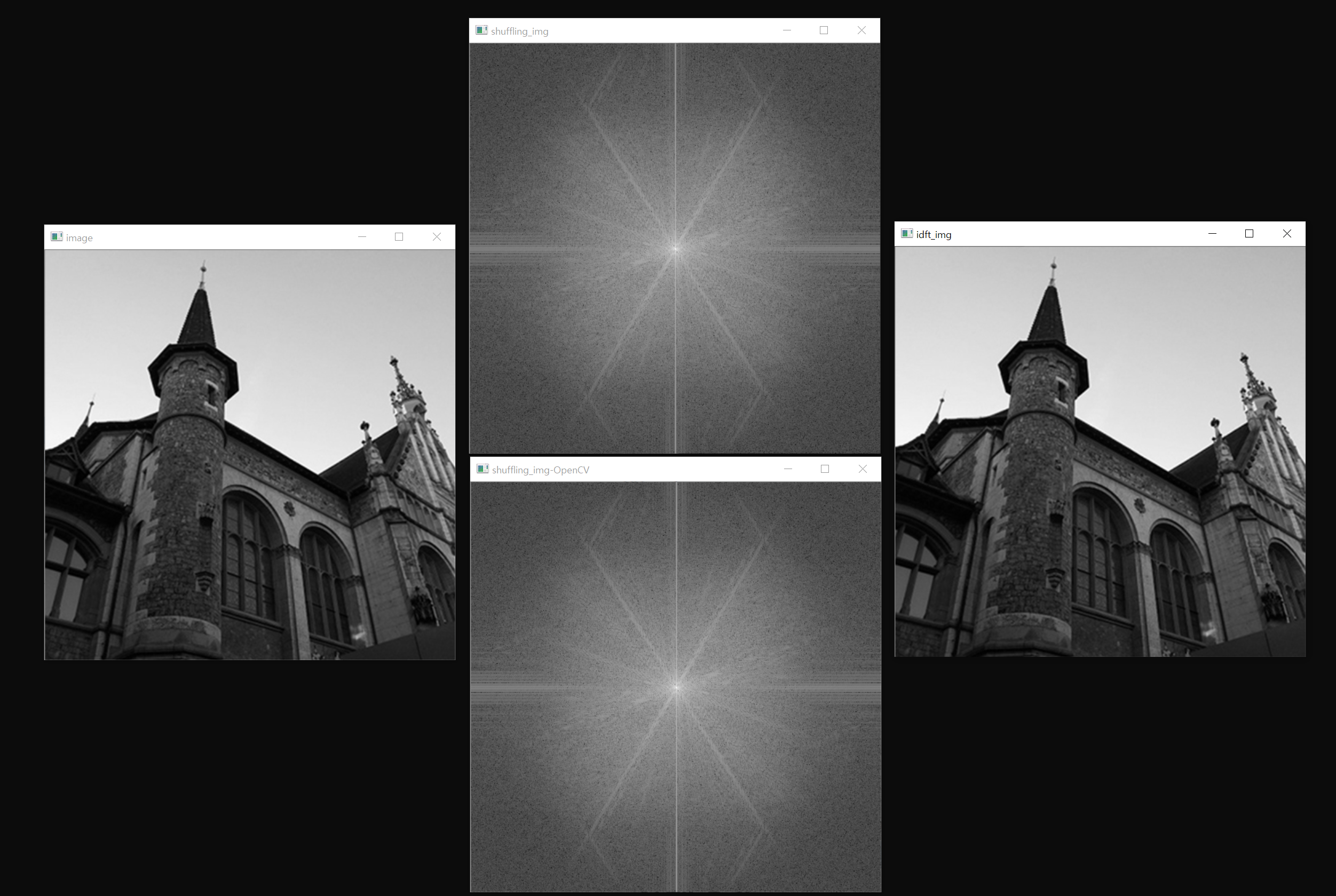
imshow("image", image);
imshow("shuffling_img", shuffling_img1);
imshow("shuffling_img-OpenCV", shuffling_img2);
imshow("idft_img", img_tmp[0]);
waitKey();
return 0;
}
10.2.4. 저주파 및 고주파 통과 필터링
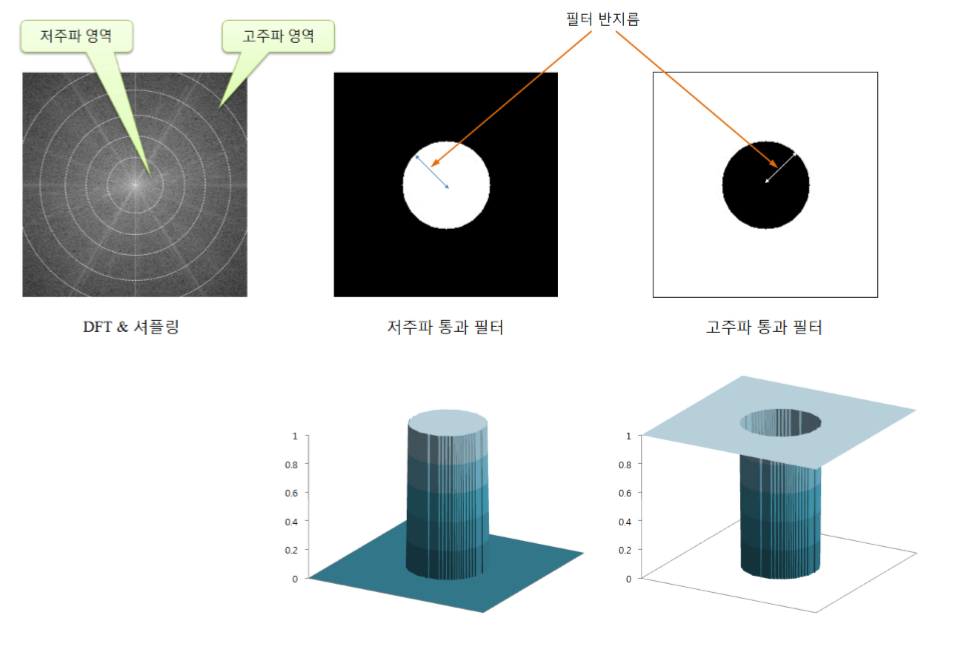
- 저주파 통과 필터링
- DFT 변환 영역에서 저주파 영역의 계수들은 통과, 고주파 영역의 계수들은 차단
- 고주파 통과 필터링
- DFT 변환 영역에서 고주파 영역의 게수들은 통과, 저주파 영역의 계수들은 차단
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void log_mag(Mat complex_mat, Mat& dst)
{
Mat planes[2];
split(complex_mat, planes);
magnitude(planes[0], planes[1], dst);
log(dst + 1, dst);
normalize(dst, dst, 0, 255, CV_MINMAX);
dst.convertTo(dst, CV_8U);
}
void shuffling(Mat mag_img, Mat& dst)
{
int cx = mag_img.cols / 2;
int cy = mag_img.rows / 2;
Rect q1(cx, 0, cx, cy); // 1사분면 사각형
Rect q2(0, 0, cx, cy); // 2사분면 사각형
Rect q3(0, cy, cx, cy); // 3사분면 사각형
Rect q4(cx, cy, cx, cy); // 4사분면 사각형
dst = Mat(mag_img.size(), mag_img.type());
mag_img(q1).copyTo(dst(q3));
mag_img(q3).copyTo(dst(q1));
mag_img(q2).copyTo(dst(q4));
mag_img(q4).copyTo(dst(q2));
}
Mat scramble(Mat signal)
{
Mat dst = signal.clone();
for (int i = 0, j = 0; i < dst.cols - 1; i++)
{
if (i > j) {
swap(dst.at<Vec2f>(i), dst.at<Vec2f>(j));
}
int m = dst.cols >> 1;
while ((j >= m) && (m >= 2))
{
j -= m;
m >>= 1;
}
j += m;
}
return dst;
}
Mat zeropadding(Mat img)
{
int m = 1 << (int)ceil(log2(img.rows));
int n = 1 << (int)ceil(log2(img.cols));
Mat dst(m, n, img.type(), Scalar(0));
Rect rect(Point(0, 0), img.size());
img.copyTo(dst(rect));
dst.convertTo(dst, CV_32F);
return dst;
}
void butterfly(Mat& dst, int dir)
{
int length = dst.cols;
int pair = 1;
for (int k = 0; k < ceil(log2(length)); k++)
{
int half_pair = pair;
pair <<= 1;
float theta = dir * (-2.0 * CV_PI / pair);
float wpr = -2.0 * sin(0.5 * theta) * sin(0.5 * theta);
float wpi = sin(theta);
float wre = 1.0;
float wim = 0.0;
for (int m = 0; m < half_pair; m++) {
for (int even = m; even < length; even += pair)
{
int odd = even + half_pair;
Vec2f G_even = dst.at<Vec2f>(even);
Vec2f G_odd = dst.at<Vec2f>(odd);
Vec2f G_odd_exp(0, 0);
G_odd_exp[0] = G_odd[0] * wre - G_odd[1] * wim;
G_odd_exp[1] = G_odd[1] * wre + G_odd[0] * wim;
dst.at<Vec2f>(even) = G_even + G_odd_exp;
dst.at<Vec2f>(odd) = G_even - G_odd_exp;
}
float tmp = wre;
wre += tmp * wpr - wim * wpi;
wim += wim * wpr + tmp * wpi;
}
}
if (dir == -1) dst /= dst.cols;
}
void FFT_2D(Mat complex_img, Mat& dst, int dir)
{
dst = Mat(complex_img.size(), complex_img.type());
for (int i = 0; i < complex_img.rows; i++)
{
Mat scr_sn = scramble(complex_img.row(i));
butterfly(scr_sn, dir);
scr_sn.copyTo(dst.row(i));
}
transpose(dst, dst);
for (int i = 0; i < dst.rows; i++) {
Mat scr_sn = scramble(dst.row(i));
butterfly(scr_sn, dir);
scr_sn.copyTo(dst.row(i));
}
transpose(dst, dst);
}
// 저주파 통과 필터 생성
Mat get_lowpassFilter(Size size, int radius)
{
Point center = size / 2;
Mat filter(size, CV_32FC2, Vec2f(0, 0));
circle(filter, center, radius, Vec2f(1, 1), -1);
return filter;
}
// 고주파 통과 필터 생성
Mat get_highpassFilter(Size size, int radius)
{
Point center = (size / 2);
Mat filter(size, CV_32FC2, Vec2f(1, 1));
circle(filter, center, radius, Vec2f(0, 0), -1);
return filter;
}
//주파수 공간 필터링 수행
void passFiltering(Mat dft_coef, Mat filter, Mat dst[2])
{
Mat filtered_mat, filtered_img, img_tmp[2];
multiply(dft_coef, filter, filtered_mat); //원소간 곱셈
log_mag(filtered_mat, dst[0]);
shuffling(filtered_mat, filtered_mat); // 역셔플링(dft_coef를 다시 역셔플링을 통해 저주파를 모서리로 보냄)
FFT_2D(filtered_mat, filtered_img, -1); //푸리에 역변환
split(filtered_img, img_tmp);
img_tmp[0].convertTo(dst[1], CV_8U);
}
void FFT(Mat image, Mat& dft_coef, Mat& dft_img) // fft 전체 과정 수행
{
Mat complex_img;
Mat pad_img = zeropadding(image); // 영삽입
Mat tmp[] = { pad_img, Mat::zeros(pad_img.size(), pad_img.type()) };
merge(tmp, 2, complex_img); // 복소 행렬 구성
FFT_2D(complex_img, dft_coef, 1); // fft 수행
// dft(complex_img, dft_coef, 0); // fft 수행
shuffling(dft_coef, dft_coef); // 셔플링
log_mag(dft_coef, dft_img); // 주파수 스펙트럼 영상
}
Mat IFFT(Mat dft_coef, Size size) // IFFT 전체 과정 수행
{
Mat idft_coef, idft_img[2];
shuffling(dft_coef, dft_coef); // 역 셔플링 수행
FFT_2D(dft_coef, idft_coef, -1);
// dft(dft_coef, idft_coef, DFT_INVERSE + DFT_SCALE);
split(idft_coef, idft_img); // 복소 행렬 분리
Rect img_rect(Point(0, 0), size);
idft_img[0](img_rect).convertTo(idft_img[0], CV_8U); // 영삽입 부분 제거
return idft_img[0];
}
int main()
{
Mat image = imread("../image/filter_test.jpg", 0);
CV_Assert(image.data);
Mat dft_coef, dft_img, low_dft, high_dft, filtered_mat1, filtered_mat2;
FFT(image, dft_coef, dft_img); // FFT 수행 및 셔플링
Mat low_filter = get_lowpassFilter(dft_coef.size(), 50); // 저주파 필터 생성
Mat high_filter = get_highpassFilter(dft_coef.size(), 20); // 고주파 필터 생성
multiply(dft_coef, low_filter, filtered_mat1); //원소간 곱셈
multiply(dft_coef, high_filter, filtered_mat2); //원소간 곱셈
log_mag(filtered_mat1, low_dft); // 주파수 스펙트럼
log_mag(filtered_mat2, high_dft);
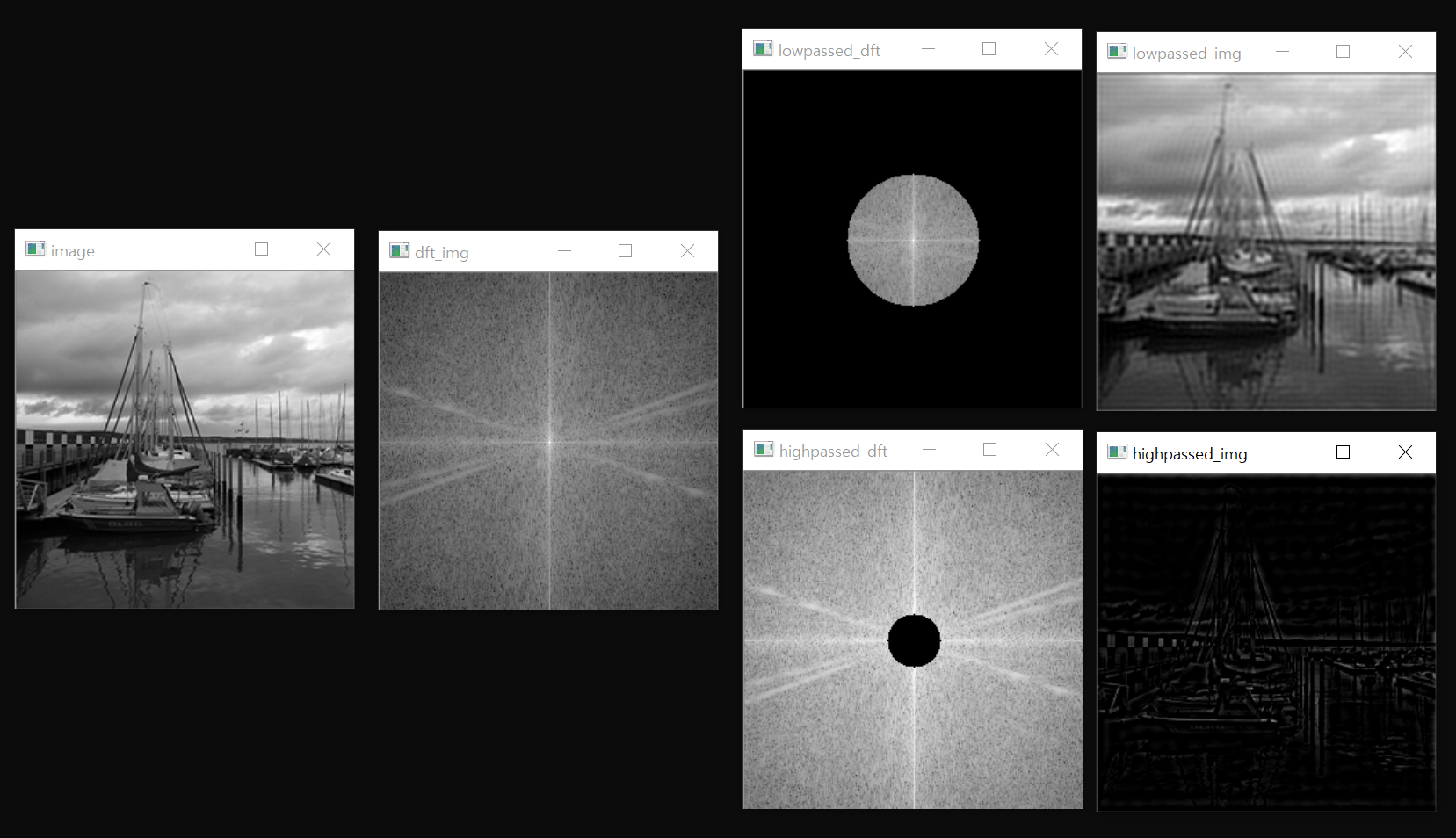
imshow("image", image);
imshow("dft_img", dft_img);
imshow("lowpassed_dft", low_dft); // 필터된 스펙트럼 영상
imshow("highpassed_dft", high_dft);
imshow("lowpassed_img", IFFT(filtered_mat1, image.size())); // 푸리에 환원 영상
imshow("highpassed_img", IFFT(filtered_mat2, image.size())); // 푸리에 환원 영상
waitKey();
return 0;
}
10.2.5. 버터워즈, 가우시안 필터링
- 대역 통과 필터(임의의 차단 주파수 계수 설정)
- 특정한 대역에서 급격하게 값을 제거하기 때문에 결과 영상의 화질 저하
- 객체의 경계부분 주위로 잔물결 같은 무늬가 나타난다.
- 해결 방법은 필터 원소값을 차단 주파수에서 급격하게 0으로 하지 않고 완만한 경사가 이루도록 버터워즈 필터나 가우시안 필터를 적용한다.
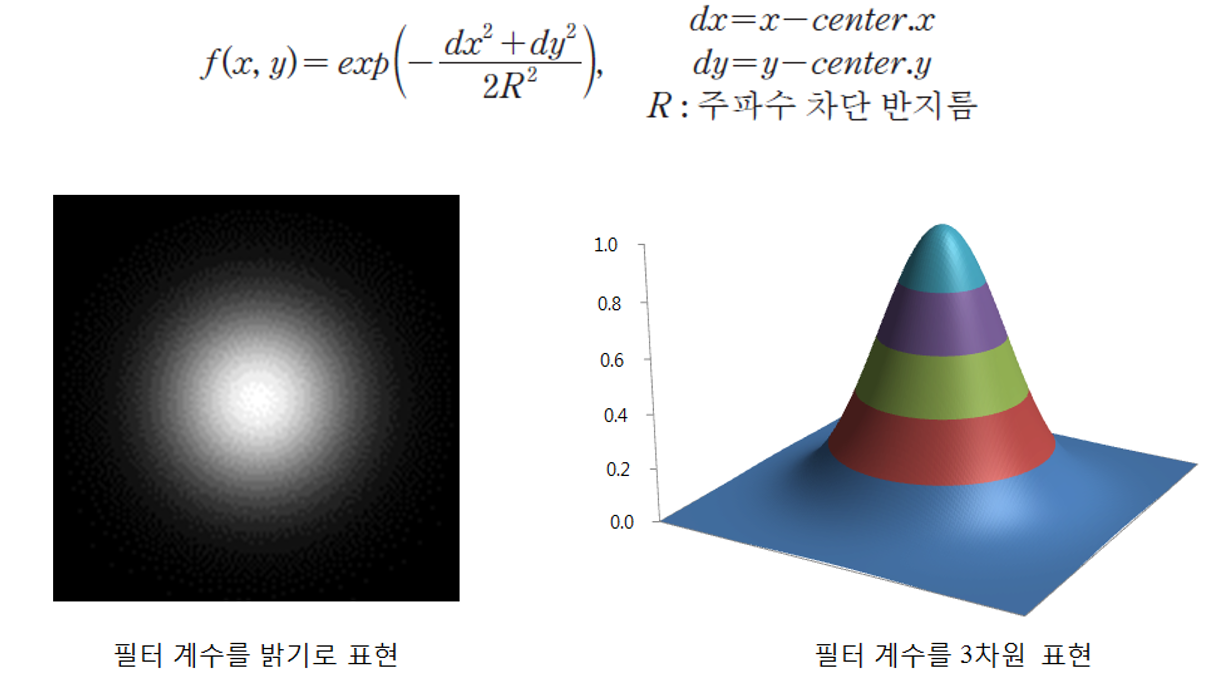
- 가우시안 필터
- 필터 원소의 구성을 가우시안 함수의 수식 분포를 갖게 함으로써 차단 주파수 부분을 점진적으로 구성한 것
- 버터워즈 필터
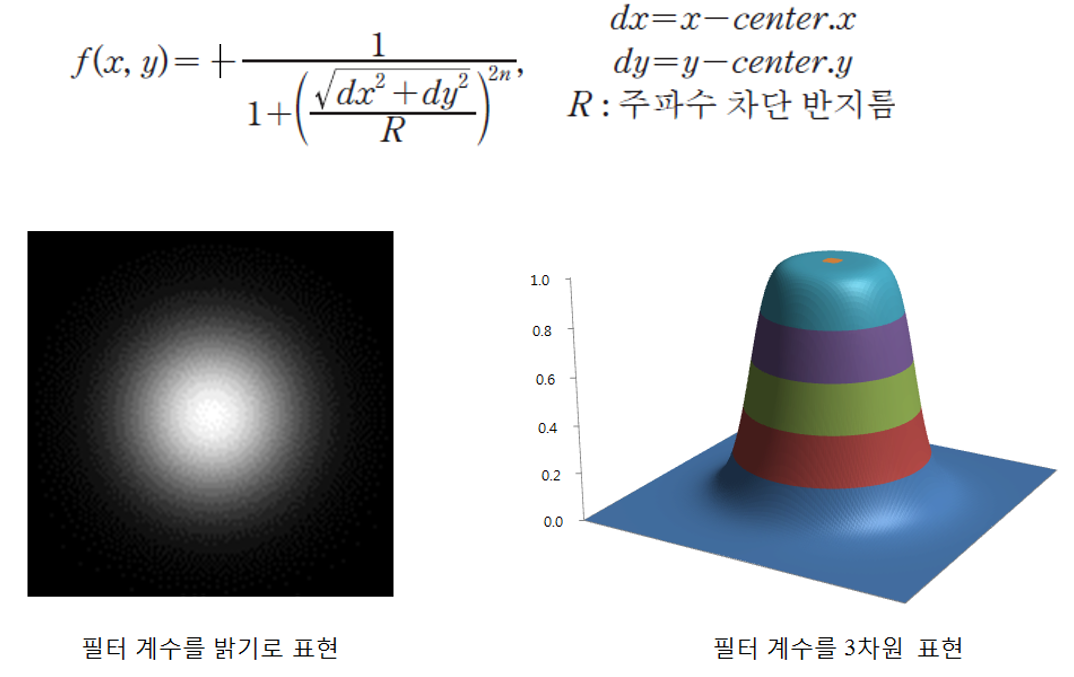
- 차단 주파수 반지름 위치(R)와 지수의 승수인 n값에 따라서 차단 필터의 반지름과 포물선의 곡률을 결정한 것
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void log_mag(Mat complex_mat, Mat& dst)
{
Mat planes[2];
split(complex_mat, planes);
magnitude(planes[0], planes[1], dst);
log(dst + 1, dst);
normalize(dst, dst, 0, 255, CV_MINMAX);
dst.convertTo(dst, CV_8U);
}
void shuffling(Mat mag_img, Mat& dst)
{
int cx = mag_img.cols / 2;
int cy = mag_img.rows / 2;
Rect q1(cx, 0, cx, cy); // 1사분면 사각형
Rect q2(0, 0, cx, cy); // 2사분면 사각형
Rect q3(0, cy, cx, cy); // 3사분면 사각형
Rect q4(cx, cy, cx, cy); // 4사분면 사각형
dst = Mat(mag_img.size(), mag_img.type());
mag_img(q1).copyTo(dst(q3));
mag_img(q3).copyTo(dst(q1));
mag_img(q2).copyTo(dst(q4));
mag_img(q4).copyTo(dst(q2));
}
Mat scramble(Mat signal)
{
Mat dst = signal.clone();
for (int i = 0, j = 0; i < dst.cols - 1; i++)
{
if (i > j) {
swap(dst.at<Vec2f>(i), dst.at<Vec2f>(j));
}
int m = dst.cols >> 1;
while ((j >= m) && (m >= 2))
{
j -= m;
m >>= 1;
}
j += m;
}
return dst;
}
Mat zeropadding(Mat img)
{
int m = 1 << (int)ceil(log2(img.rows));
int n = 1 << (int)ceil(log2(img.cols));
Mat dst(m, n, img.type(), Scalar(0));
Rect rect(Point(0, 0), img.size());
img.copyTo(dst(rect));
dst.convertTo(dst, CV_32F);
return dst;
}
void butterfly(Mat& dst, int dir)
{
int length = dst.cols;
int pair = 1;
for (int k = 0; k < ceil(log2(length)); k++)
{
int half_pair = pair;
pair <<= 1;
float theta = dir * (-2.0 * CV_PI / pair);
float wpr = -2.0 * sin(0.5 * theta) * sin(0.5 * theta);
float wpi = sin(theta);
float wre = 1.0;
float wim = 0.0;
for (int m = 0; m < half_pair; m++) {
for (int even = m; even < length; even += pair)
{
int odd = even + half_pair;
Vec2f G_even = dst.at<Vec2f>(even);
Vec2f G_odd = dst.at<Vec2f>(odd);
Vec2f G_odd_exp(0, 0);
G_odd_exp[0] = G_odd[0] * wre - G_odd[1] * wim;
G_odd_exp[1] = G_odd[1] * wre + G_odd[0] * wim;
dst.at<Vec2f>(even) = G_even + G_odd_exp;
dst.at<Vec2f>(odd) = G_even - G_odd_exp;
}
float tmp = wre;
wre += tmp * wpr - wim * wpi;
wim += wim * wpr + tmp * wpi;
}
}
if (dir == -1) dst /= dst.cols;
}
void FFT_2D(Mat complex_img, Mat& dst, int dir)
{
dst = Mat(complex_img.size(), complex_img.type());
for (int i = 0; i < complex_img.rows; i++)
{
Mat scr_sn = scramble(complex_img.row(i));
butterfly(scr_sn, dir);
scr_sn.copyTo(dst.row(i));
}
transpose(dst, dst);
for (int i = 0; i < dst.rows; i++) {
Mat scr_sn = scramble(dst.row(i));
butterfly(scr_sn, dir);
scr_sn.copyTo(dst.row(i));
}
transpose(dst, dst);
}
void FFT(Mat image, Mat& dft_coef, Mat& dft_img) // fft 전체 과정 수행
{
Mat complex_img;
Mat pad_img = zeropadding(image); // 영삽입
Mat tmp[] = { pad_img, Mat::zeros(pad_img.size(), pad_img.type()) };
merge(tmp, 2, complex_img); // 복소 행렬 구성
FFT_2D(complex_img, dft_coef, 1); // fft 수행
// dft(complex_img, dft_coef, 0); // fft 수행
shuffling(dft_coef, dft_coef); // 셔플링
log_mag(dft_coef, dft_img); // 주파수 스펙트럼 영상
}
Mat IFFT(Mat dft_coef, Size size) // IFFT 전체 과정 수행
{
Mat idft_coef, idft_img[2];
shuffling(dft_coef, dft_coef); // 역 셔플링 수행
FFT_2D(dft_coef, idft_coef, -1);
// dft(dft_coef, idft_coef, DFT_INVERSE + DFT_SCALE);
split(idft_coef, idft_img); // 복소 행렬 분리
Rect img_rect(Point(0, 0), size);
idft_img[0](img_rect).convertTo(idft_img[0], CV_8U); // 영삽입 부분 제거
return idft_img[0];
}
//가우시안 저주파 통과 필터
Mat getGausianFilter(Size size, int _sigma)
{
Point center = size / 2;
Mat filter(size, CV_32FC2, Vec2f(0, 0));
double sigma = 2 * _sigma * _sigma;
for (int i = 0; i < size.height; i++) {
for (int j = 0; j < size.width; j++)
{
// 중심점에서 계산
int x = pow(j - center.x, 2);
int y = pow(i - center.y, 2);
float result = exp((float)(-(x + y) / sigma));
filter.at<Vec2f>(i, j) = Vec2f(result, result);
}
}
return filter;
}
//버터워즈 저주파 통과 필터
Mat getButterworthFilter(Size size, int D, int n)
{
Point center = size / 2;
Mat filter(size, CV_32FC2, Vec2f(0, 0));
for (int i = 0; i < size.height; i++) {
for (int j = 0; j < size.width; j++)
{
int x = pow(j - center.x, 2);
int y = pow(i - center.y, 2);
float result = 1 / (1 + pow((float)sqrt(x + y) / D, 2 * n));
filter.at<Vec2f>(i, j) = Vec2f(result, result);
}
}
return filter;
}
int main()
{
Mat image = imread("../image/filter_test.jpg", 0);
CV_Assert(image.data);
Mat dft_coef, dft_img, filtered_mat1, filtered_mat2, gauss_dft, butter_dft;
FFT(image, dft_coef, dft_img); // FFT 수행 및 셔플링
Mat gauss_filter = getGausianFilter(dft_coef.size(), 30);
Mat butter_filter = getButterworthFilter(dft_coef.size(), 30, 4);
multiply(dft_coef, gauss_filter, filtered_mat1); //원소간 곱셈
multiply(dft_coef, butter_filter, filtered_mat2); //원소간 곱셈
log_mag(filtered_mat1, gauss_dft); // 주파수 스펙트럼
log_mag(filtered_mat2, butter_dft);
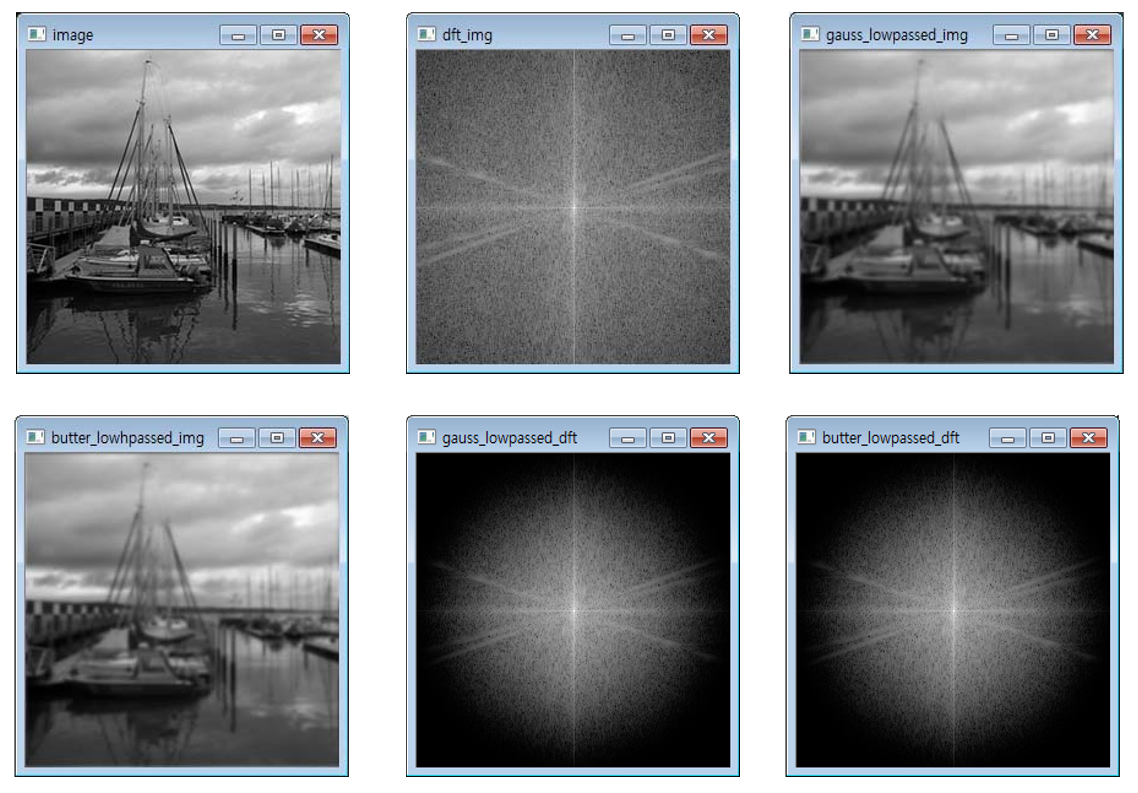
imshow("image", image);
imshow("dft_img", dft_img);
imshow("gauss_lowpassed_dft", gauss_dft);
imshow("butter_lowpassed_dft", butter_dft);
imshow("gauss_lowpassed_img", IFFT(filtered_mat1, image.size()));// IFFT 환원 영상
imshow("butter_lowhpassed_img", IFFT(filtered_mat2, image.size()));
waitKey();
return 0;
}
*/
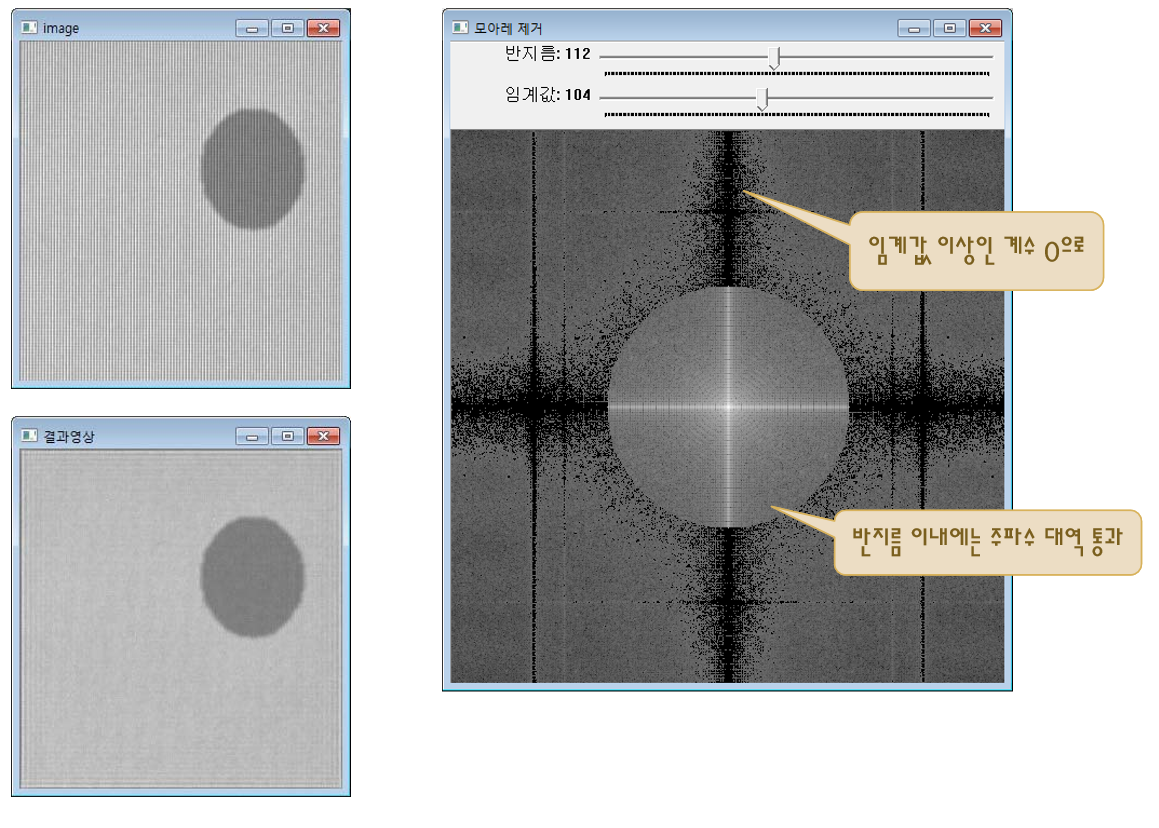
10.2.6. 모아레 제거
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
#include "fft.hpp"
Mat image, dft_coef, spectrum_img;
int radius, thres = 120;
void remove_moire(int value, void* userdata)
{
Mat remove_mask, remv_dft_coef, spectrum_tmp;
// 주파수 제거 위한 마스크 생성
threshold(spectrum_img, remove_mask, thres, 255, THRESH_TOZERO_INV);
// threshold(remove_mask, remove_mask, 1, 255, THRESH_BINARY);
circle(remove_mask, remove_mask.size() / 2, radius, Scalar(255), -1);
dft_coef.copyTo(remv_dft_coef, remove_mask);
log_mag(remv_dft_coef, spectrum_tmp); // 모아레 제거된 스펙트럼
Rect img_rect(Point(0, 0), image.size());
imshow("모아레 제거", spectrum_tmp);
imshow("결과영상", IFFT(remv_dft_coef, image.size()));
}
int main()
{
image = imread("../image/mo3.jpg", 0);
CV_Assert(image.data);
FFT(image, dft_coef, spectrum_img);
radius = dft_coef.rows / 4;
imshow("image", image);
imshow("모아레 제거", spectrum_img);
createTrackbar("반지름", "모아레 제거", &radius, 255, remove_moire);
createTrackbar("임계값", "모아레 제거", &thres, 255, remove_moire);
waitKey();
return 0;
}