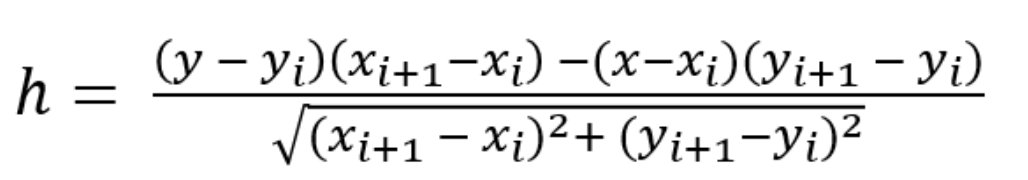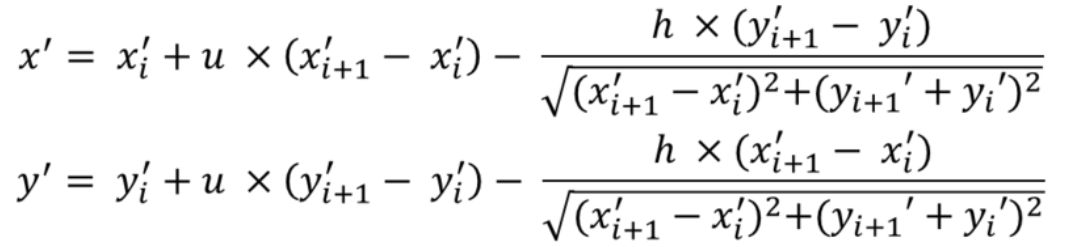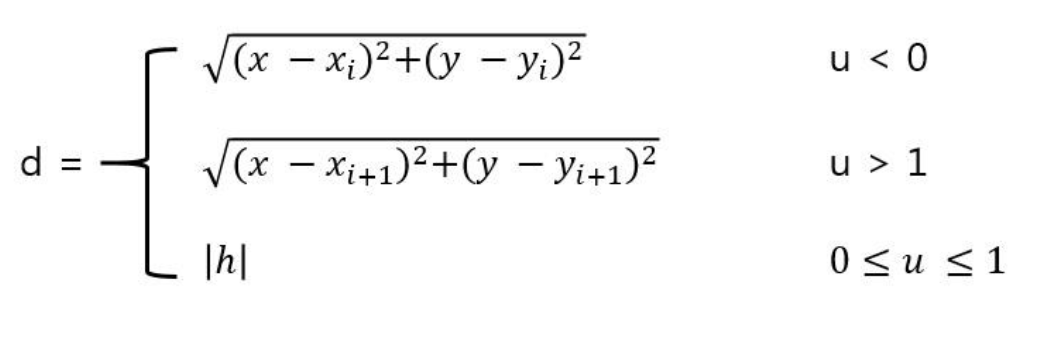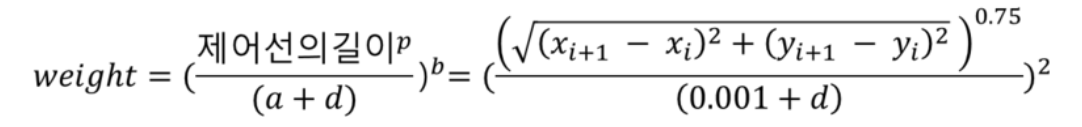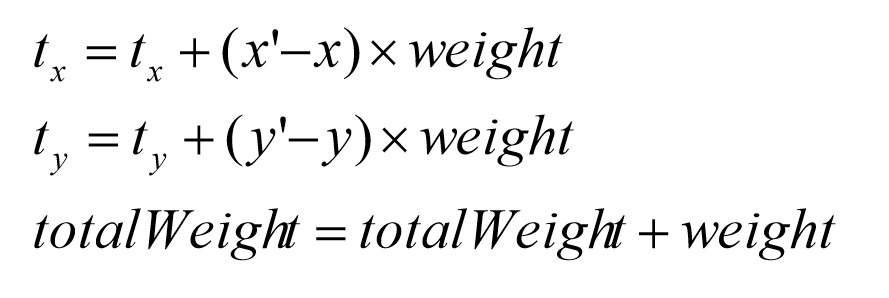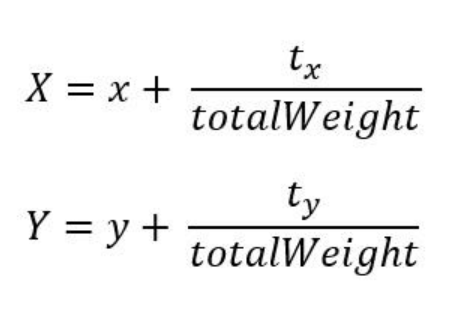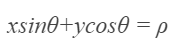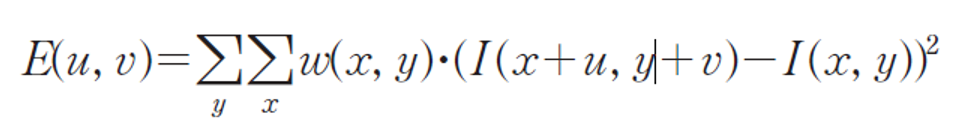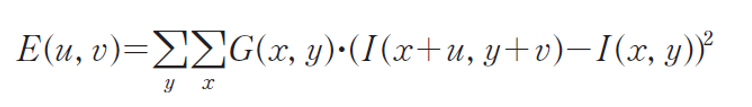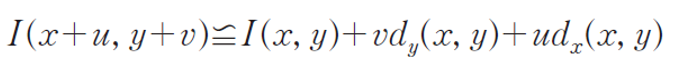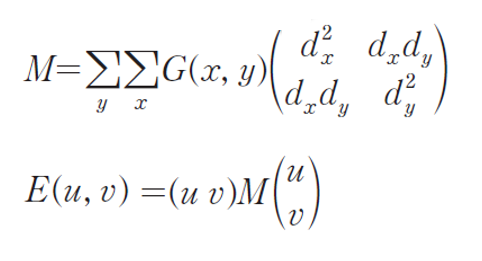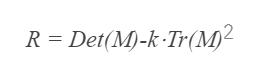Visual C++ 영상 처리 프로그래밍 gaussian37님의 영상 워핑
11. 영상 워핑과 모핑, 그리고 Feature 검출인식 및 실습
11.1. 영상 워핑과 모핑
11.1.1. 영상 워핑(Warping)
- 픽셀의 위치를 이동하는 기하학적 처리 중 한 기법이다.
- 회전, 이동, 확대/축소 등의 기하학적 처리는 모든 픽셀에 대해 일정한 규칙을 적용함으로써 균일한 반환 결과를 얻지만, 영상 워핑은 픽셀별로 이동 정도를 달리할 수 있어 고무판 위에 그려진 영상을 임의대로 구부리는 효과를 나타낼 수 있다.
- 인공위성이나 우주선으로부터 전공된 영상은 렌즈의 변형, 신호의 왜곡 등의 이유로 인해 일그러지는 경우가 많은데, 영상 워핑은 이러한 일그러짐을 복구하는데 사용한다.

- 입력 영상과 출력 영상의 대응관계 기술
- 제어선, 제어점, 그물망, 다각형 등을 이용
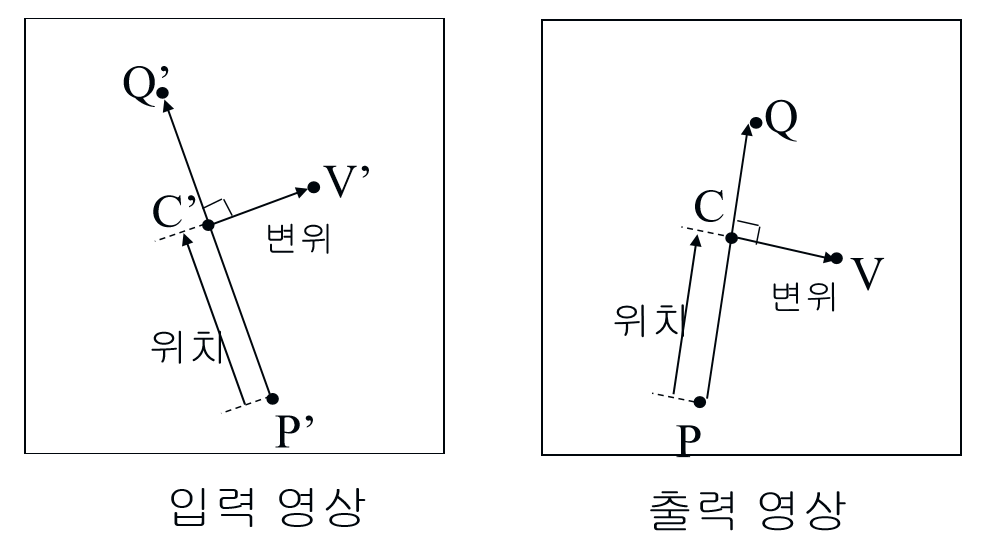
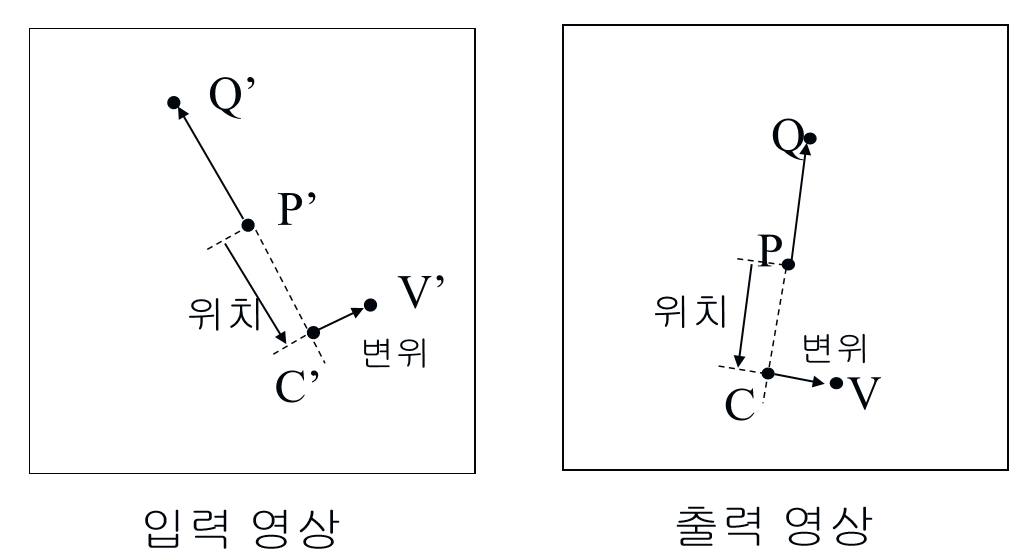
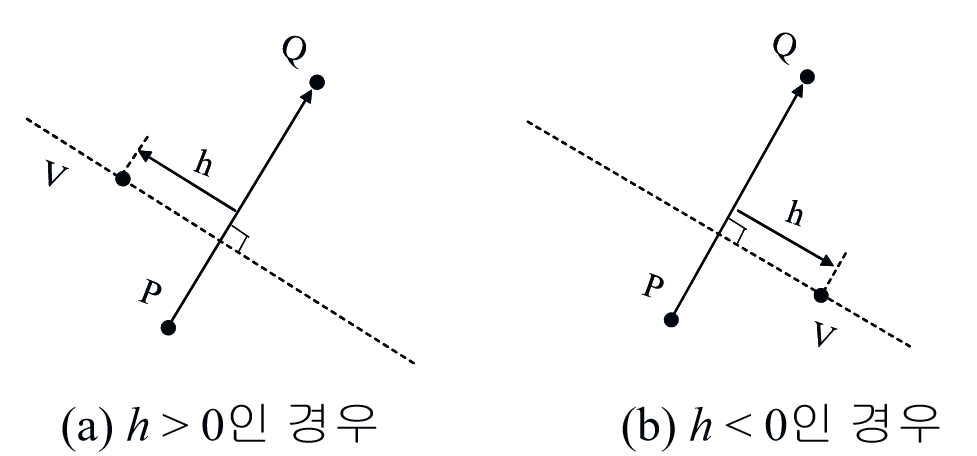
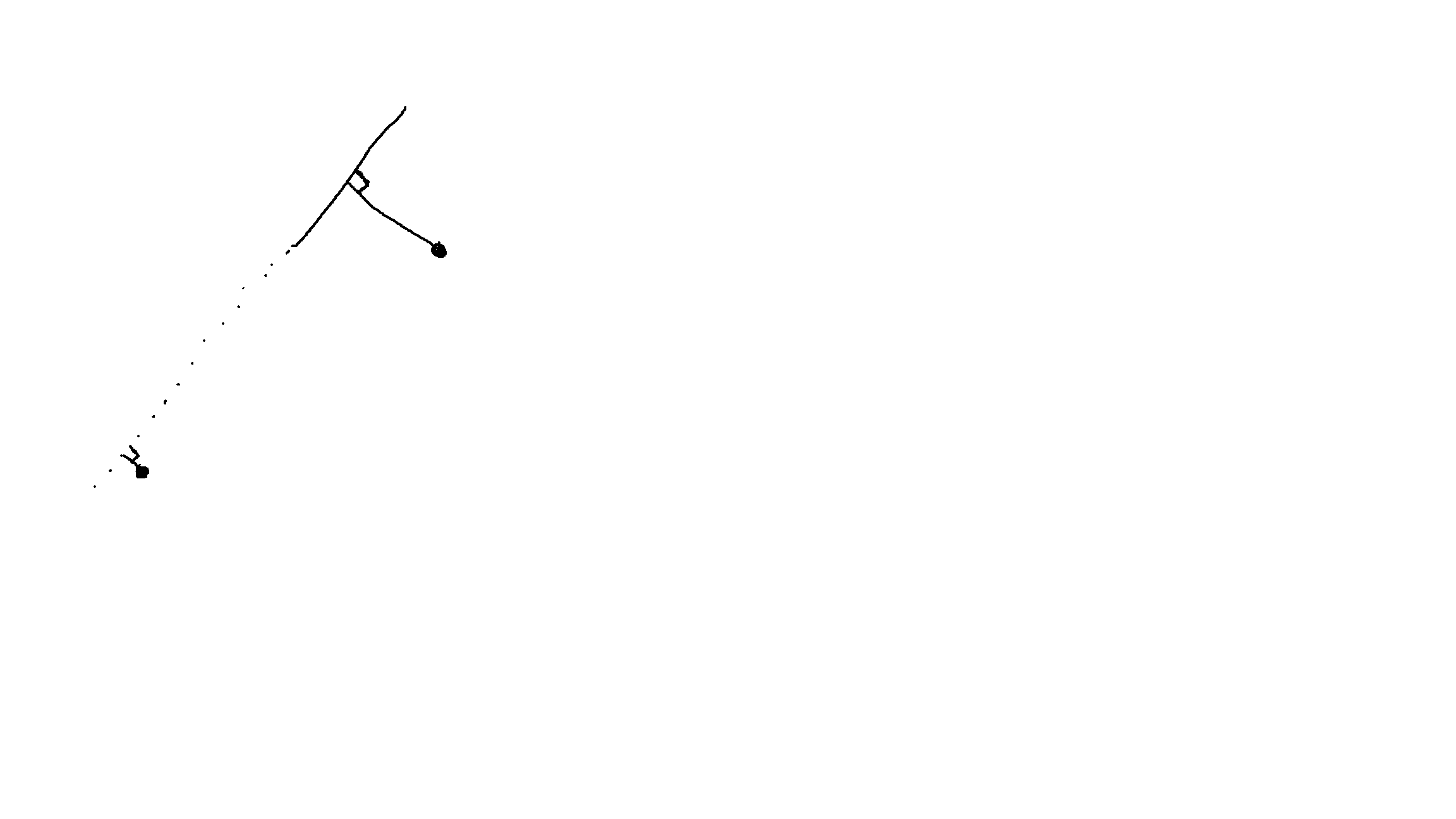
- 제어선을 이용하는 경우 아래의 그림과 같이 화소와 제어선 사이의 수직 교차점을 구한다. 그리고 화소와 수직 교차점 사이의 변위 정보와 제어선 내에서 수직 교차점의 위치 정보 두 가지를 활용하고, 역방향 사상을 이용하여 워핑을 수행한다.
- 수직 교차점이 제어선 내부에 있는 경우로, 출력 영상에서 제어선 PQ가 입력 영상에서 제어선 P’Q’에 대응되고, 출력 영상의 픽셀 V가 입력 영상의 픽셀 V’에 대응된다. 역방향 사상에 의하여 픽셀 V에 대응되는 V’의 위치를 계산하기 위해서 PQ내에서의 C의 상대적 위치와 동일하게 P’Q’내에서 C’의 위치를 찾는다. 그 다음에 C와 V사이의 변위만큼 C’으로부터 떨어진 점 V’를 찾는다.
- 수직 교차점이 제어선 외부에 있는 경우로, 동일하게 역방향 사상으로 구한다.
- 하나의 제어선에 대해서는 단순하게 픽셀의 이동 위치를 계산할 수 있지만, 여러 개의 제어선이 사용될 수 있다. 제어선이 여러 개일 경우에는 각 제어선은 영상의 모든 픽셀에 영향을 미치게 된다.
- 한 픽셀이 여러 개의 제어선으로부터 영향받는 것을 반영하기 위해 가중치를 사용한다.
- 제어선의 길이가 길수록 가중치가 커지고, 픽셀과 제어선 사이의 거리가 가까울수록 가중치가 커진다.
- b값이 커지면 픽셀들은 먼 거리에 있는 제어선들로부터 영향을 적게 받게 된다.
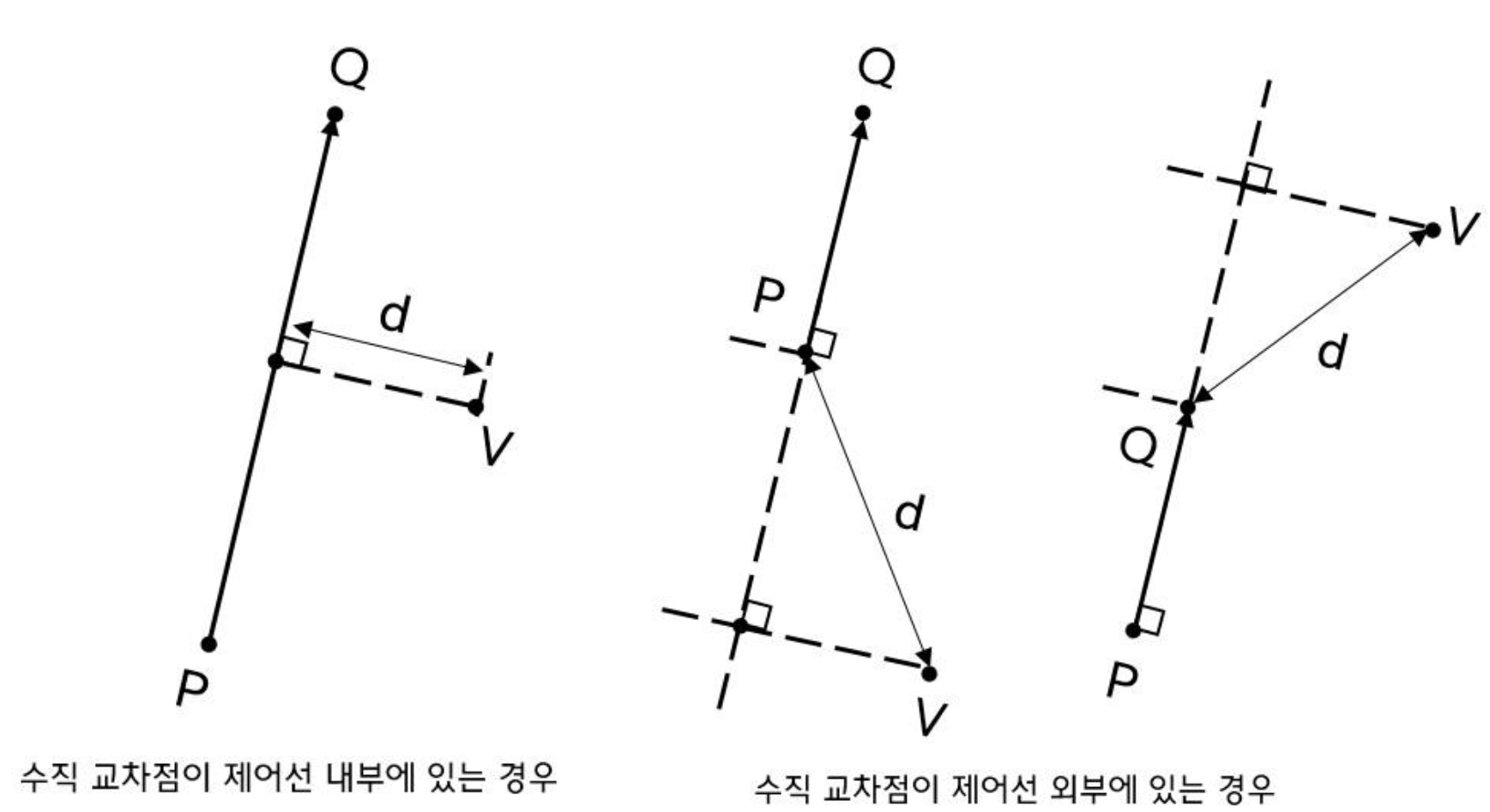
- 픽셀과 제어선의 거리는 수직 교차점의 위치에 따라 다르게 정의된다. 수직 교차점이 제어선 내부에 있는 경우에는 픽셀과 수직 교차점 사이의 거리가 사용되지만, 제어선 외부에 있는 경우에는 제어선의 양 끝점 중에서 픽셀과 가까운 점과 픽셀 사이의 거리가 사용된다.
- 만약 픽셀이 제어선 외부에 있지만 제어선과 가깝다고 가중치를 많이 주게되면, 영향을 이상하게 받을 수 있기 때문이다.
- 제어선이 여러 개인 경우의 출력 영상의 각 픽셀에 대한 입력 영상의 대응 픽셀을 구하는 warping() 함수의 알고리즘
- 워핑 영상 알고리즘 순서
1) 수직 교차점의 위치 계산
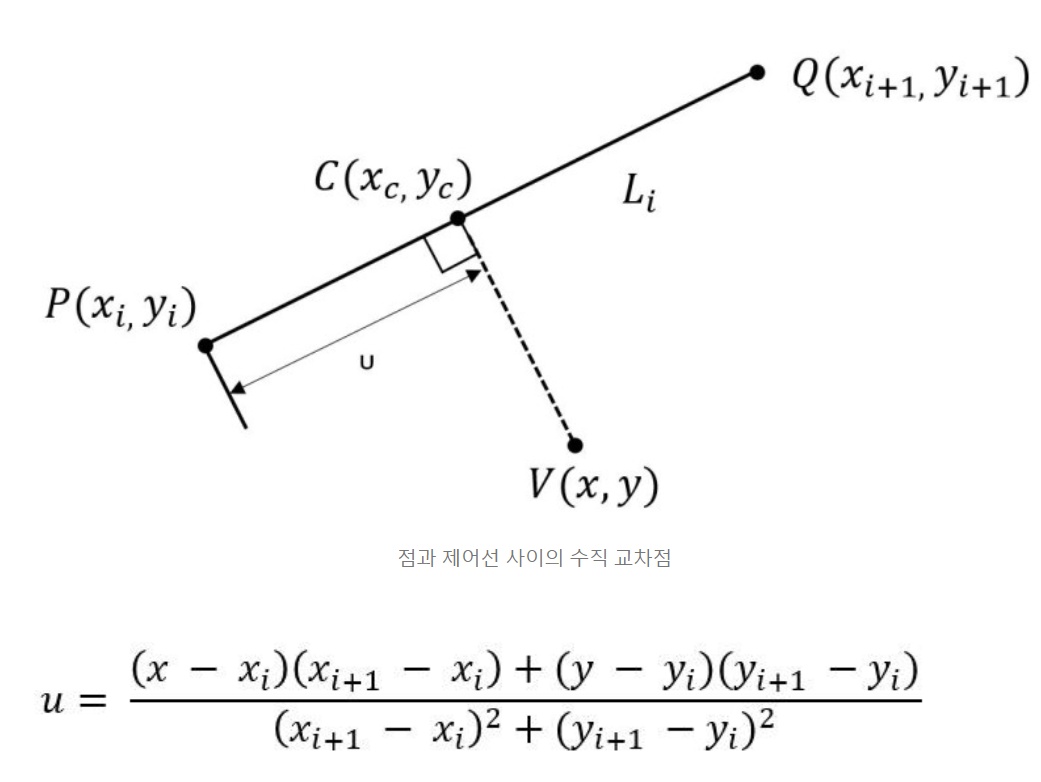
- 각 픽셀 V(x, y)에 대하여 각각의 제어선 \(L_i\)와의 수직 교차점의 위치를 구한다.
- V(x, y)에서 제어선 \(L_i\)에 내린 수선의 점 \(C(x_c, y_c)\)와 \(P(x_i, y_i)\) 사이의 거리를 u라 하면, u의 길이는 다음과 같다.
- u의 값은 수직 교차점의 위치에 따라 다음과 같은 범위의 값을 가진다.
2) 제어선으로부터의 수직 변휘 계산
- 출력 영상의 픽셀 V(x, y)에 대하여 각각의 제어선 \(L_i\)로부터의 수직 변위를 구한다.
- 변위 h의 값은 다음과 같은 범위를 가진다.
- 변위의 절대값은 수직 교차점과 픽셀 사이의 거리가 된다. 변위의 절대값이 아닌 제어선과 픽셀의 위치를 알기 위해서 변위를 구할 때, 절대값을 사용하지 않는다.
3) 입력 영상에서의 대응 픽셀 위치 계산
- 출력 영상의 각 픽셀 V(x, y)에 대해 각각의 제어선 \(L_i\)와의 수직 교차점의 위치 u와 수직 변위 h를 구한 다음, u와 h값을 이용하여 출력 영상의 V(x, y)에 대응되는 입력 영상의 픽셀 V’(x’, y’)을 찾는다.
- 출력 영상의 제어선 \(L_i\)에 대응되는 입력 영상에서의 제어선 \(L_i'\)의 양 끝점 좌표를 \((x_i', y_i')과 (x_(i+1)', y_(i+1)')\)이라고 하면 V’(x’, y’)은 다음 식과 같다.
4) 픽셀과 제어선 사이의 거리 계산
5) 제어선의 가중치 계산
- a, b, p의 상수값은 일반적으로 각각 0.001, 2.0, 0.75를 사용한다.
6) 입력 영상의 대응 픽셀과의 변위 누적
- 각 제어선 \(L_i\)에 대해 출력 영상의 픽셀 V(x, y)에 대응되는 입력 영상의 픽셀 V’(x’, y’)을 구하고, 가중치 weight을 구한 다음에 다음 식과 같이 V와 V’사이의 변위와 가중치의 곱을 계산하여 t_x, t_y 변수에 누적한다.
7) 입력 영상의 대응 픽셀 위치 계산 - 각 제어선에 대해 출력 영상의 픽셀 V(x, y)에 대응되는 입력 영상의 픽셀의 변위값을 구하여 이들의 합 \((t_x, t_y)\)를 계산한 다음에는 다음 식에 의해 V(x, y)에 대응되는 입력 영상의 픽셀 V(X, Y)의 위치를 계산한다.
- 워핑 영상 알고리즘 순서
11.1.2. 영상 모핑(Morphing)
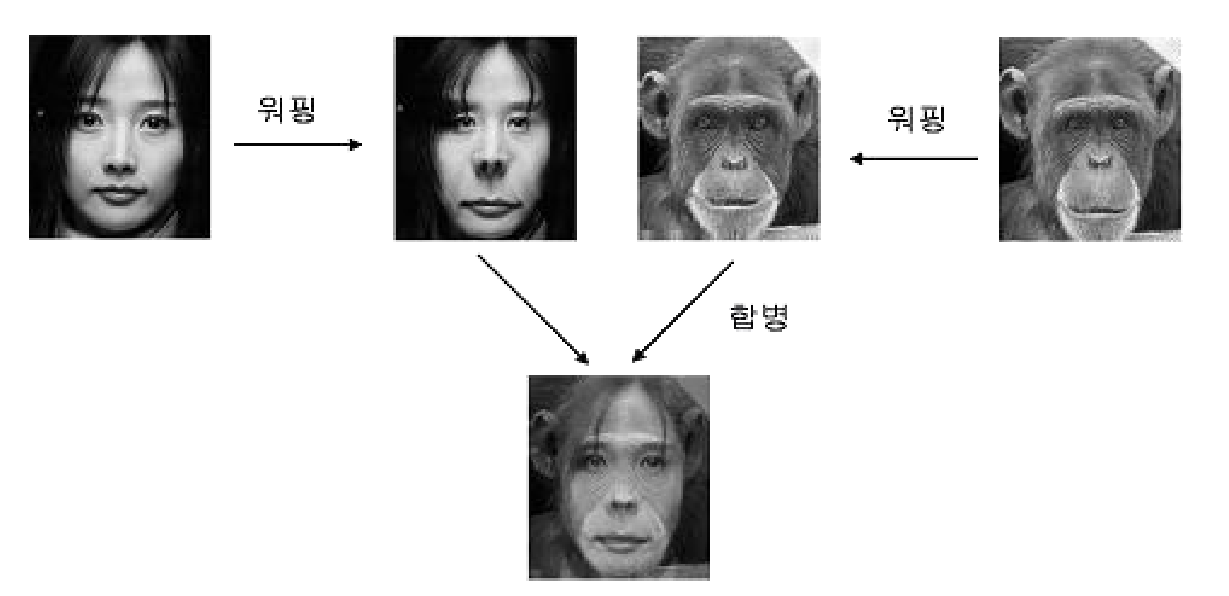
- 모핑은 하나의 형체가 전혀 다른 이미지로 변화하는 기법이다. 즉, 두 개의 서로 다른 이미지나 3차원 모델 사이의 변화하는 과정을 서서히 나타내는 것이다.
- 모핑은 워핑과 합병의 두 단계로 구성된다.
- 모핑을 위해서는 두 영상 사이의 대응 위치를 기술해야 한다.
- 워핑 단계
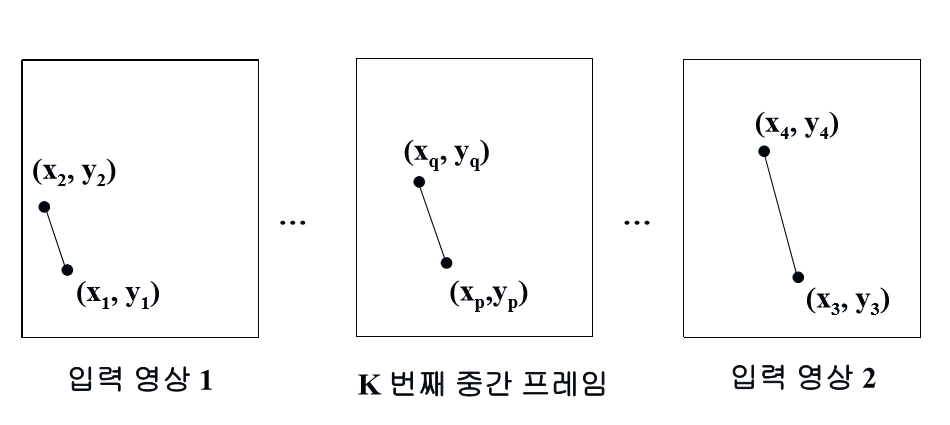
- 두 입력 영상의 제어선으로부터 보간법을 사용하여 생성한다.
- K번째 중간 프레임에 대한 제어선을 계산하면 다음과 같다.
- 합병 단계
- 워핑 단계를 거쳐 구해진 제어선을 다음 식으로 계산하여 합병한다.
11.2. Feature 검출인식 및 실습
11.2.1. 허프 변환 직선 검출
- 직선은 영상에서 찾을 수 있는 특징 중 가장 중요한 정보를 제공한다.
- 영상에서 직선 성분을 찾기 위해서는 우선 엣지 픽셀의 위치를 찾아내고, 이러한 엣지 픽셀들이 직선의 방정식에 맞게 일렬로 배열되어 있는지를 확인해야 한다.
- 주로 직선 검출은 허프 변환 기법을 사용한다.
- 허프 변환은 2차원 공간에서의 직선의 방정식으로 파라미터 공간으로 변환하여 직선을 찾는 알고리즘이다.
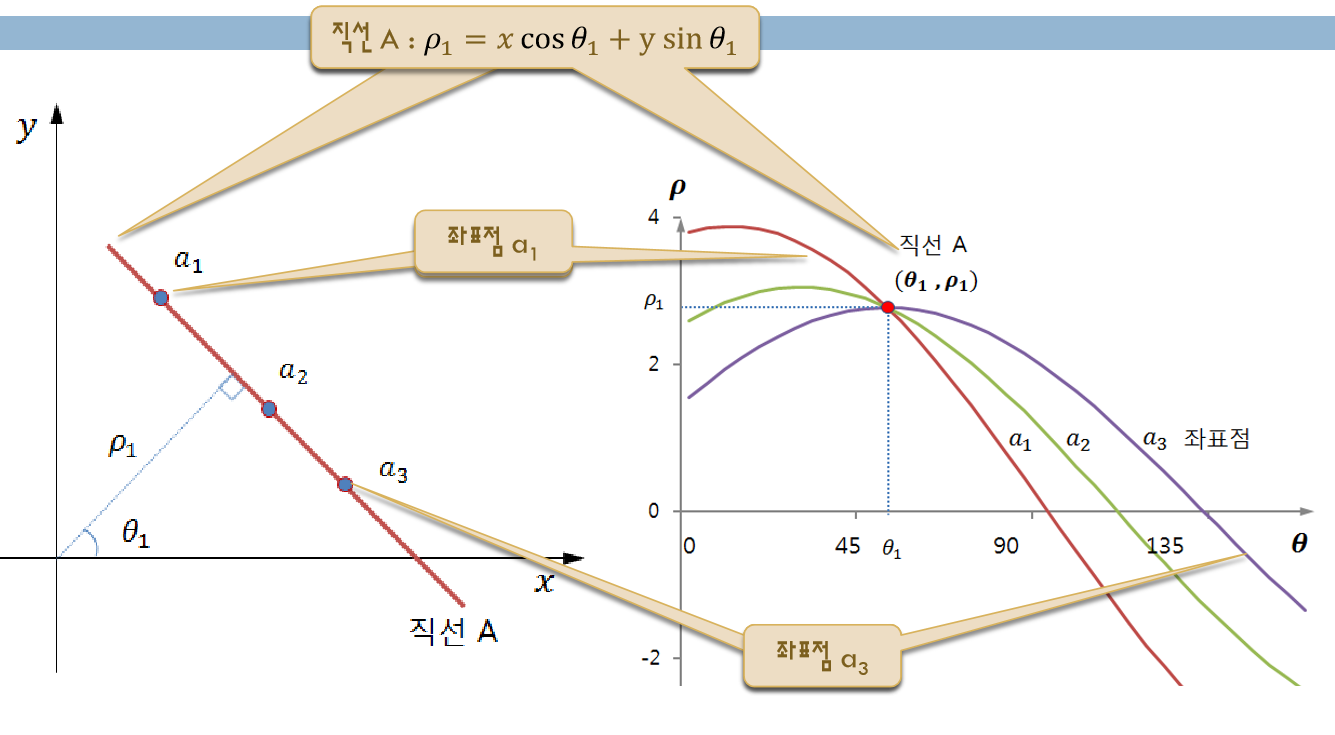
- 가장 기본적인 식인 y = ax + b는 xy 좌표 공간에서 a라는 기울기값과 b라는 절편값으로 표현되지만, 반대로 ab 좌표 공간에서 x와 y값을 구할 수도 있다. 허프 변환은 이러한 현상을 이용하여 xy공간에서의 직선을 찾는다.
- 예를 들어 다음 아래의 그림과 같이, xy 좌표 공간에서 직선의 방정식인 y = a’x + b’에 포함되는 점 \((x_i, y_i), (x_j, y_j)\)가 있다. 이들은 각각 ab 공간에서 오른쪽 직선으로 표현될 수 있다.
- 즉, xy 공간에서 직선에 있는 점들을 이용하여 생성한 ab 공간상의 직선들은 모두 (a’, b’)을 지나간다.
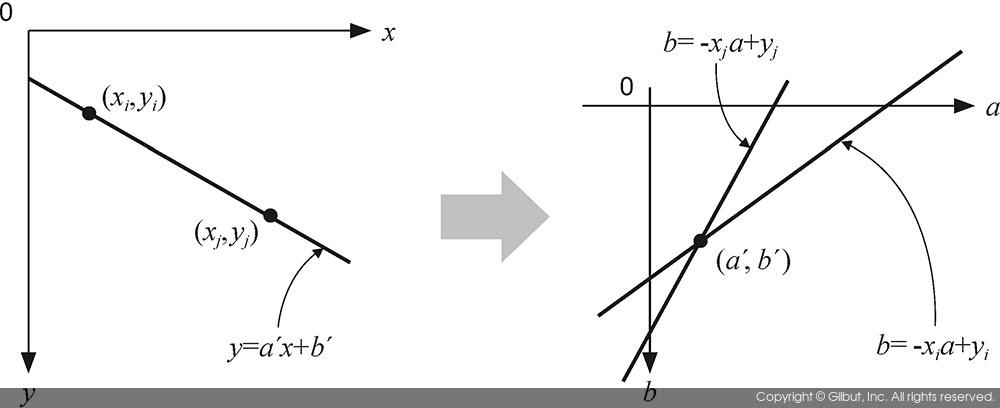
- 허프 변환을 이용하여 직선의 방정식을 찾으려면 xy 공간에서 에지로 판별된 모든 점을 이용하여 ab 파라미터 공간에 직선을 표현하고, 직선이 많이 교차되는 좌표를 모두 찾아야 한다.
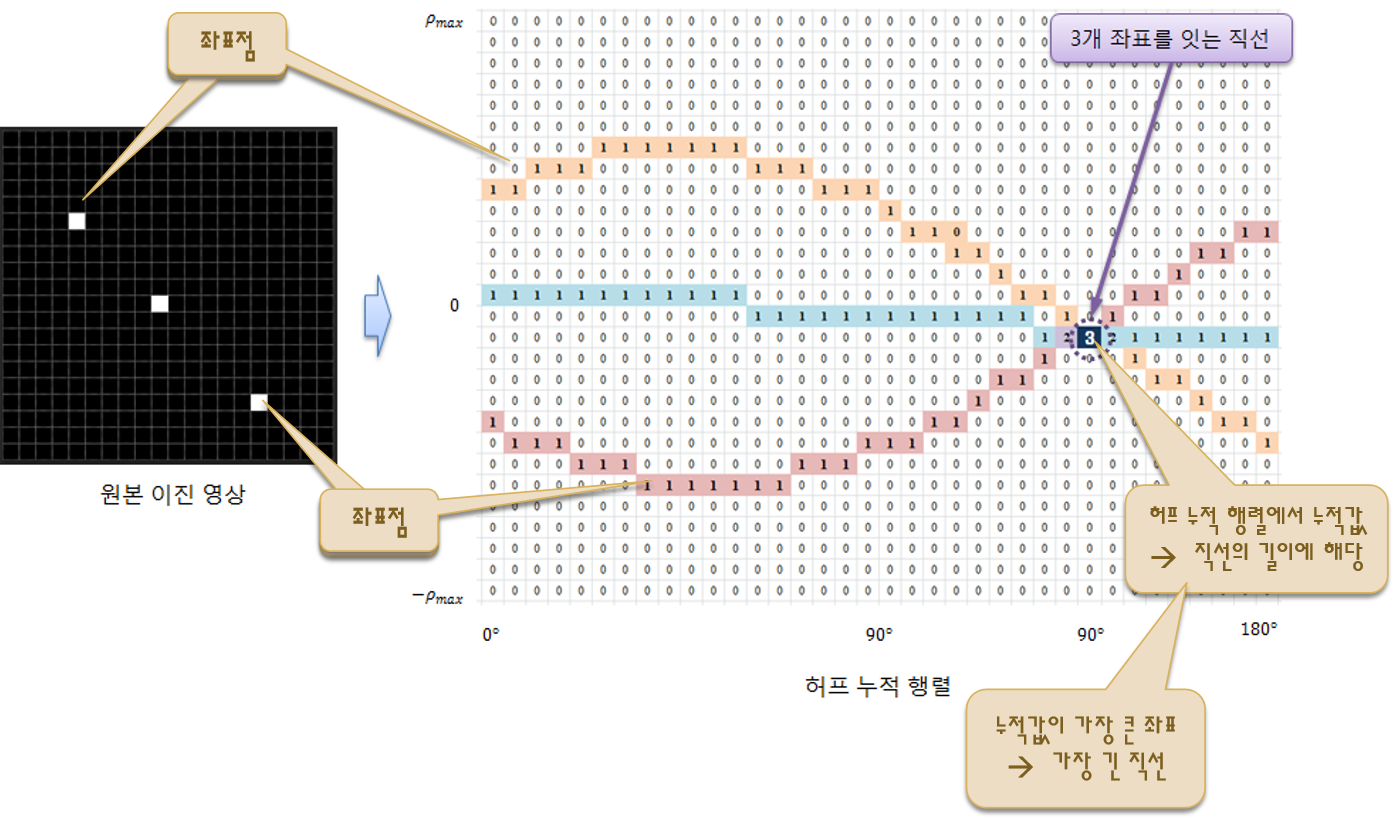
- 이때, 직선이 많이 교차하는 점을 찾기 위해서 보통 축적 배열(accumulation array)을 사용한다. 축적 배열은 0으로 초기화된 2차원 배열에서 직선이 지나가는 위치의 배열 원소값을 1씩 증가시켜 생성한다.
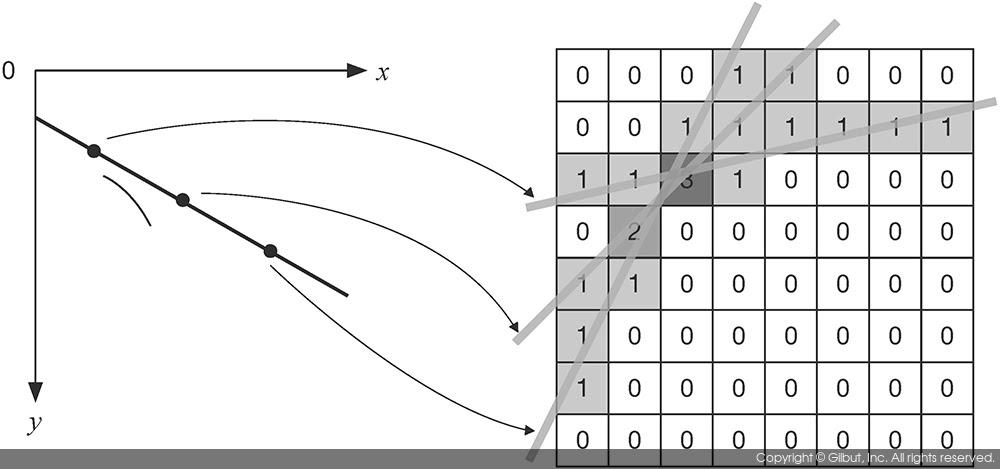
- 그러나 y = ax + b 형태의 직선의 방정식을 사용할 경우에 모든 형태의 직선을 표현하기 어렵기 때문에 극좌표계 형식의 직선의 방정식을 사용한다.
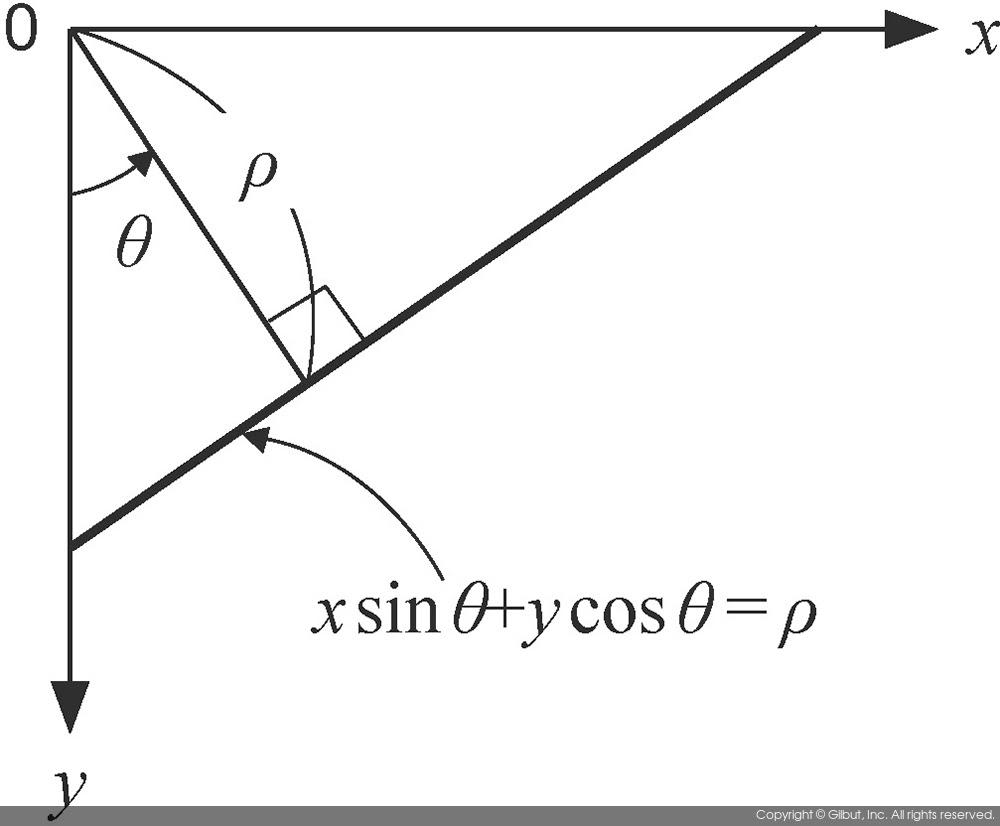
- 위 수식에서 p는 원점 (0, 0)에서 직선까지의 수직 거리를 의미하고, \(\Theta\)는 원점에서 직선에 수직선을 그렸을 때 y축과 이루는 각도의 크기를 의미한다.
- 이 경우 xy 공간에서 한 점은 \(p\Theta\) 공간에서는 삼각함수 그래프 형태의 공선으로 표현되고, \(p\Theta\) 공간에서 한 점은 xy 공간에서 직선으로 나타나게 된다.
- 극좌표계 형식의 직선의 방정식에서도 축적 배열을 사용하여 허프 변환을 수행하고, 축적 배열에서 국지적 최댓값이 발생하는 위치에서의 p와 \(\Theta\)를 찾아 직선의 방정식을 구할 수 있다.
- p와 \(\Theta\)는 실수값을 가지기 때문에 축적 배열을 구현하려면 p와 \(\Theta\)가 가질 수 있는 값의 범위를 적당한 크기로 나눠서 저장하는 양자화(quantization) 과정을 거쳐야 한다.
- 예를 들어 \(\Theta\)는 0부터 \(\pi\) 사이의 실수를 가질 수 있는데, 이 구간을 180단계 혹은 360단계로 나눌 수 있다. 구간을 촘촘하게 나누면, 정밀한 직선 검출이 가능하지만 연산 시간이 늘어날 수 있다.
-
허프 변환의 전체 과정은 다음과 같다.
1) 허프 변환 좌표계에서 행렬 구성
2) 영상 내 모든 화소의 직선 여부 검사
3) 직선 인지 좌표에 대한 허프 변환 누적 행렬 구성
4) 허프 누적 행렬의 지역 최댓값 선정(한 지점에서 여러 직선이 검출될 경우를 방지하기 위해 국지적 최댓값을 구한다)
5) 임계값 이상인 누적값(직선) 선별
6) 직선 \((P_i, \Theta_i)\)을 누적값 기준으로 내림차순 정렬
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void hough_coord(Mat image, Mat& acc_mat, double rho, double theta)
{
int acc_h = int((image.rows + image.cols) * 2 / rho); // 피타고라스 정리로 구한 수직선보다 살짝 더 큰 범위인 width + height로 범위를 설정
int acc_w = int(CV_PI / theta);
acc_mat = Mat(acc_h, acc_w, CV_32S, Scalar(0));
for (int i = 0; i < image.rows; i++) {
for (int j = 0; j < image.cols; j++)
{
Point pt(j, i); // 조회 좌표
if (image.at<uchar>(pt) > 0) { // 직선 여부 검사
for (int t = 0; t < acc_w; t++) // 행렬의 인덱스이므로 라디안이 필요
{
// pt(j, i)가 0보다 큰 값은 곧, 점을 뜻하므로, 점을 지나는 직선 방정식 구하기
double radian = t * theta;
double r = pt.x * cos(radian)+ pt.y * sin(radian);
r = cvRound(r / rho + acc_mat.rows / 2.0); // rho를 나누는 이유는 theta와 같은 이유(허프 좌표계에서 y값 역시 그냥 상수이지만, 좌표로 봤을 때는 인덱스값이기 때문에)
acc_mat.at<int>((int)r, t)++;
}
}
}
}
}
void acc_mask(Mat acc_mat, Mat& acc_dst, Size size, int thresh)
{
acc_dst = Mat(acc_mat.size(), CV_32S, Scalar(0)); // 마스크 적용 후의 결과영상 구하기
Point h_m = size / 2; // 마스크 크기 절반
for (int r = h_m.y; r < acc_mat.rows - h_m.y; r++) {
for (int t = h_m.x; t < acc_mat.cols - h_m.x; t++)
{
Point center = Point(t, r) - h_m;
int c_value = acc_mat.at<int>(center); // 입력영상(아까 위에서 만들어준 누적 허프 변환 행렬)의 중심화소
if (c_value >= thresh)
{
// 마스크만큼 정해준 영역에 대해서 순회하면서
double maxVal = 0;
for (int u = 0; u < size.height; u++) {
for (int v = 0; v < size.width; v++)
{
Point start = center + Point(v, u);
if (start != center && maxVal < acc_mat.at<int>(start))
maxVal = acc_mat.at<int>(start);
}
}
// 정해준 영역에서 가장 큰 값만 남기고, 나머지는 0으로 변환
Rect rect(center, size);
if (c_value >= maxVal)
{
acc_dst.at<int>(center) = c_value;
acc_mat(rect).setTo(0);
}
}
}
}
}
// 아까와 반대의 메커니즘
// 아까는 실좌표계에서 허프 변환 좌표계로 변환하는 과정이었다면,
// 여기서부터는 다시 마스크를 씌운 허프 변환 좌표계에서 구한 제일 가능성 높은 직선들을 다시 실좌표계로 변환하는 과정
void thres_lines(Mat acc_dst, Mat& lines, double _rho, double theta, int thresh)
{
for (int r = 0; r < acc_dst.rows; r++) {
for (int t = 0; t < acc_dst.cols; t++)
{
float value = (float)acc_dst.at<int>(r, t); // 누적값
if (value >= thresh) // 직선 길이 임계값
{
float rho = (float)((r - acc_dst.rows / 2) * _rho); // 수직거리 -> 위에 과정과 반대, 아까 acc_dst.rows / 2를 더했던 이유는 rho값이 음수가 될 수 있기 때문에
// 더했지만, 이번에는 반대로 실좌표계이므로 음수가 나와도 되기에 빼는 것. 또한, 다시 _rho를 아까는 곱했다면 이번에는 다시 나누기
float radian = (float)(t * theta); // 각도
Matx13f line(rho, radian, value); // 단일 직선
lines.push_back((Mat)line);
}
}
}
}
// lines에는 라디안(theat)값과 로우값들이 있음 -> 위에서 벡터 형태로 쌓았기 때문에
// sorting을 하는 이유는, 여러 개의 직선이 생기는 데, 그 중 몇 개만 추출하고 싶을 때를 위해서
void sort_lines(Mat lines, vector<Vec2f>& s_lines)
{
Mat acc = lines.col(2), idx;
sortIdx(acc, idx, SORT_EVERY_COLUMN + SORT_DESCENDING);
for (int i = 0; i < idx.rows; i++)
{
int id = idx.at<int>(i);
float rho = lines.at<float>(id, 0); // 로우 값
float radian = lines.at<float>(id, 1); // 라디안 값
s_lines.push_back(Vec2f(rho, radian)); // 정렬된 직선 벡터 - 누적값 내림차순
}
}
void houghLines(Mat src, vector<Vec2f>& s_lines, double rho, double theta, int thresh)
{
Mat acc_mat, acc_dst, lines;
hough_coord(src, acc_mat, rho, theta);
acc_mask(acc_mat, acc_dst, Size(3, 7), thresh);
thres_lines(acc_dst, lines, rho, theta, thresh);
sort_lines(lines, s_lines);
}
void draw_houghLines(Mat image, Mat& dst, vector<Vec2f> lines, int nline)
{
if (image.channels() == 3) image.copyTo(dst);
else cvtColor(image, dst, COLOR_GRAY2BGR);
for (int i = 0; i < min((int)lines.size(), nline); i++)
{
float rho = lines[i][0], theta = lines[i][1];
double a = cos(theta), b = sin(theta);
Point2d delta(1000 * -b, 1000 * a);
Point2d pt(a * rho, b * rho);
line(dst, pt + delta, pt - delta, Scalar(0, 255, 0), 1, LINE_AA);
}
}
int main()
{
Mat image = imread("../image/hough_test.jpg", 0);
CV_Assert(image.data);
Mat canny, dst1, dst2;
GaussianBlur(image, canny, Size(5, 5), 2, 2);
Canny(canny, canny, 100, 150, 3);
double rho = 1, theta = CV_PI / 180;
vector<Vec2f> lines1, lines2;
houghLines(canny, lines1, rho, theta, 50);
// HoughLines(canny, lines2, rho, theta, 50);
draw_houghLines(canny, dst1, lines1, 10);
// draw_houghLines(canny, dst2, lines2, 10);
imshow("source", image);
imshow("canny", canny);
imshow("detected lines", dst1);
// imshow("detected lines_OpenCV", dst2);
waitKey();
}
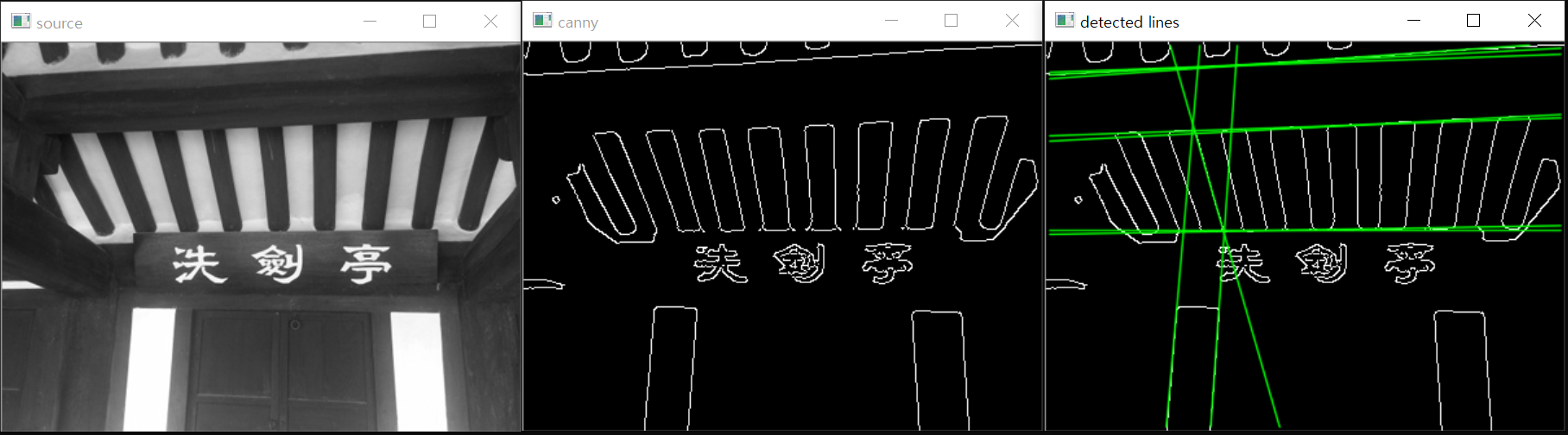
11.2.2. 허프 변환 원 검출
- 중심 좌표가 (a, b)이고 반지름이 r인 원의 방정식은 (x-a)^2 + (y-b)^2 = r^2이다.
- 원의 방정식은 세 개의 파라미터를 가지고 있으므로, 허프 변환을 적용하려면 3차원 파라미터 공간에서 축적 배열을 정의하고 가장 누적이 많은 위치를 찾아야 한다.
- 그러나 3차원 파라미터 공간에서 축적 배열을 정의하고 사용하려면 너무 많은 메모리와 연산 시간이 필요하기 때문에 허프 변환 대신 허프 그래디언트 방법을 사용한다.
-
허프 그래디언트 방법(Hough gradient method)
1) 영상에 존재하는 모든 원의 중심 좌표 찾기 -> 축적 배열
2) 검출된 원의 중심으로부터 원에 적합한 반지름 구하기 - 원의 중심을 찾기 위해 입력 영상의 모든 에지 픽셀에서 그래디언트를 구하고, 그래디언트 방향을 따르는 직선의 축적 배열값을 1씩 증가시킨다.
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main(void) {
Mat src = imread("../image/test.jpg", IMREAD_GRAYSCALE);
CV_Assert(src.data);
Mat blurred;
medianBlur(blurred, src, 5);
Mat dst;
cvtColor(src, dst, COLOR_GRAY2BGR);
vector<Vec3f> circles;
HoughCircles(blurred, circles, HOUGH_GRADIENT, 1, 20, 50, 35, 0, 0);
for (size_t i = 0; i < circles.size(); i++) {
Vec3i c = circles[i];
Point center(c[0], c[1]);
int radius = c[2];
circle(src, center, radius, Scalar(0, 0, 255), 2);
circle(src, center, 2, Scalar(0, 0, 255), 3);
}
imshow("src", src);
imshow("dst", dst);
waitKey(0);
return 0;
}
11.2.3. 허프 변환 심화 예제
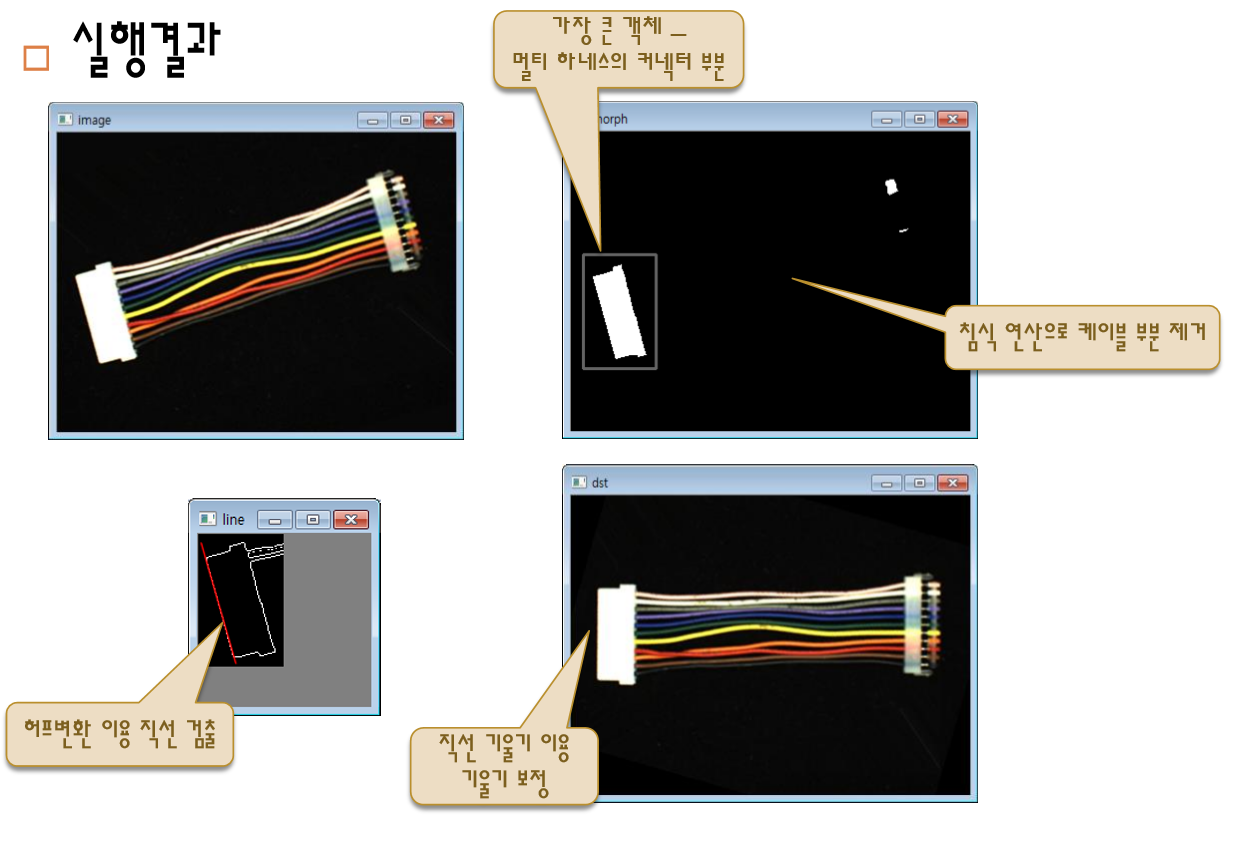
멀티 하네스의 기울기 보정
#include "hough.hpp"
// 가장 큰 객체 사각형 검색
void max_object(Mat img, Rect& rect)
{
vector<vector<Point>> contours;
findContours(img.clone(), contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE); // 외곽선 검출
int max_area = 0;
for (int i = 0; i < (int)contours.size(); i++) // 가장 큰 영역 가져오기
{
Rect r = boundingRect(contours[i]); // 외곽선 영역 포함 사각형
// 최대 크기 사각형 찾기
if (max_area < r.area()) {
max_area = r.area();
rect = r;
}
}
rect = rect - Point(10, 10) + Size(20, 20);
}
int main()
{
Rect rect(Point(0, 0), Point(10, 10));
Mat gray, canny, morph, th_gray, canny_line, dst;
double rho = 1, theta = CV_PI / 180; // 허프변환 거리간격, 각도간격
vector<Vec2f> lines; // 허프 검출 라인들
Mat image = imread("../image/5.tif", 1);
CV_Assert(image.data);
imshow("image", image);
cvtColor(image, gray, CV_BGR2GRAY); // 명암도 영상 변환
imshow("gray", gray);
threshold(gray, th_gray, 240, 255, THRESH_BINARY); //이진 영상 변환
imshow("th_gray", th_gray);
erode(th_gray, morph, Mat(), Point(-1, -1), 2); // 침식 연산
imshow("morph", morph);
max_object(morph, rect); // 가장 큰 객체 검색
rectangle(morph, rect, Scalar(255), 2); // 검색 객체 표시
imshow("rect", th_gray(rect));
// 커넥터 영역만 캐니 에지 수행
Canny(th_gray(rect), canny, 40, 100);
houghLines(canny, lines, rho, theta, 50);
draw_houghLines(canny, canny_line, lines, 1);
imshow("line", canny_line);
double angle = (CV_PI - lines[0][1]) * 180 / CV_PI; // lines[0][1]에는 theta값이 들어있음 -> 회전 각은 왜 이렇게 되나?
Point center = image.size() / 2;
Mat rot_map = getRotationMatrix2D(center, -angle, 1);
warpAffine(image, dst, rot_map, image.size(), INTER_LINEAR);
imshow("dst", dst);
resizeWindow("line", 150, 150);
waitKey(0);
return 0;
}
11.2.4. 코너 검출
- 코너 검출
- 에지나 직선은 영상 구조 파악 및 객체 검출에는 도움이 되지만, 영상 매칭에는 큰 도움이 되지 않는다. 에지 강도와 방향 정보만 가지고 있기에 영상 매칭하기엔 정보가 부족하다.
- 영상에서 특징(feature)이란 영상으로부터 추출할 수 있는 유용한 정보를 의미하며 평균 밝기, 히스토그램, 에지, 직선 성분, 코너 등이 있다.
- 영상의 특징 중에서 에지, 직선 성분, 코너처럼 영상 전체가 아닌 일부 영역에서 추출할 수 있는 특징을 지역 특징(local feature)이라 한다.
- 영상의 지역 특징 중 코너는 에지의 방향이 급격하게 변하는 부분으로서 삼각형의 꼭지점이나 연필 심처럼 뾰족하게 튀어나와 있는 부분이 된다.
- 코너는 에지나 직선 성분 등의 다른 지역 특징에 비해 분별력이 높고 대체로 영상 전 영역에 골고루 분포하기 때문에 영상을 분석하는 데 유용한 지역 특징으로 사용한다.
- 코너처럼 한 점의 형태로 표현할 수 있는 특징을 특징점(feature point)라고 하며, 특징점은 키포인트(key point) 또는 관심점(interest point)라고 부르기도 한다.
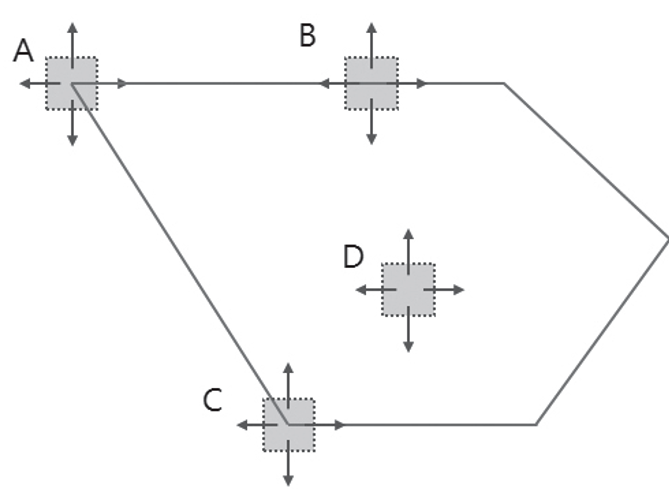
- 영상의 밝기 변화는 어느 위치에 따라 변화가 다르다.
- A, C - 모든 방향에서 밝기 변화가 크다.
- B - 한 방향(위쪽)으로 밝기 변화가 크다.
- D - 밝기 변화가 상대적으로 적다.
- 해리스 코너 검출
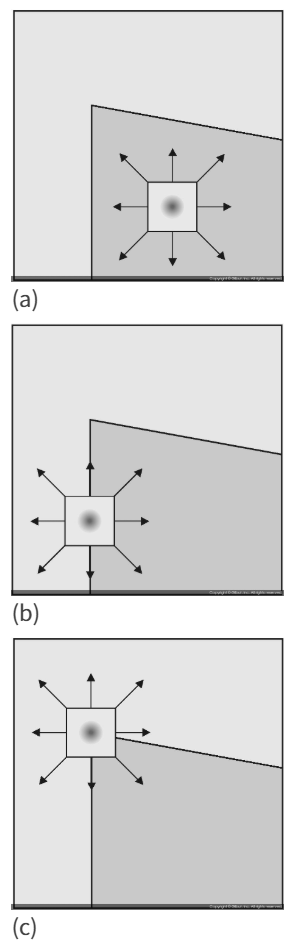
- 해리스 코너 검출 방법은 기본적으로 작은 윈도우를 상하좌우로 움직이며 윈도우 안의 픽셀값의 변화를 분석하여 코너인지 아닌지를 판별한다.
- (a)는 영상 내의 평탄한 영역에서 윈도우가 움직이는 경우로, 픽셀값이 균일한 영역에서는 윈도우 안에서의 픽셀값은 항상 일정할 것이다.
- (b)는 엣지 위치에 윈도우가 존재하는 경우로, 윈도우가 좌우로 움직이면 픽셀값의 변화가 있지만, 상하로 움직이는 경우에는 변화가 없다.
- (c)는 윈도우가 엣지에 걸쳐있는 경우로, 상하좌우 어느 방향으로 움직여도 그 안에 있는 값의 변화가 크게 나타난다.
- 이러한 방식으로 코너 위치를 판별할 수 있으며, 해리스 코너 검출기의 동작 방식이다.
- 해리스 코너 검출 알고리즘
- 모라벡(Moravec)의 방법
- 영상의 변화량(SSD, Sum of Squared Difference)로, 특정 윈도우를 이용하여 주변 픽셀과의 차이값을 나타내는 수식이다.
- 현재 화소에서 u, v 방향으로 이동했을 때의 밝기 변화량의 제곱을 나타내며, (u, v)는 상하좌우의 방향으로 한정된다.
- 문제는 0과 1의 값만을 가지는 이진 윈도우의 사용으로 노이즈에 취약하며, 4개의 방향으로만 한정시켰기 때문에 45도 간격의 에지만을 고려하는 문제가 있다.
- 해리스의 방법
- 이진 윈도우 w(u, v) 대신에 점진적으로 변화하는 가우시안 마스크 G(x, y)를 적용시켰으며, 모든 방향에서 검출할 수 있도록 미분을 도입하였다.
- 위의 수식에서 (u, v)만큼 이동된 위치에서의 픽셀값 I(x+u, y+v)는 테일러 급수(Taylor series)에 의해 다음과 같이 근사될 수 있다.
- 이 식을 다시 첫 번쩨 수식에 대입하여 정리하면 다음과 같다.
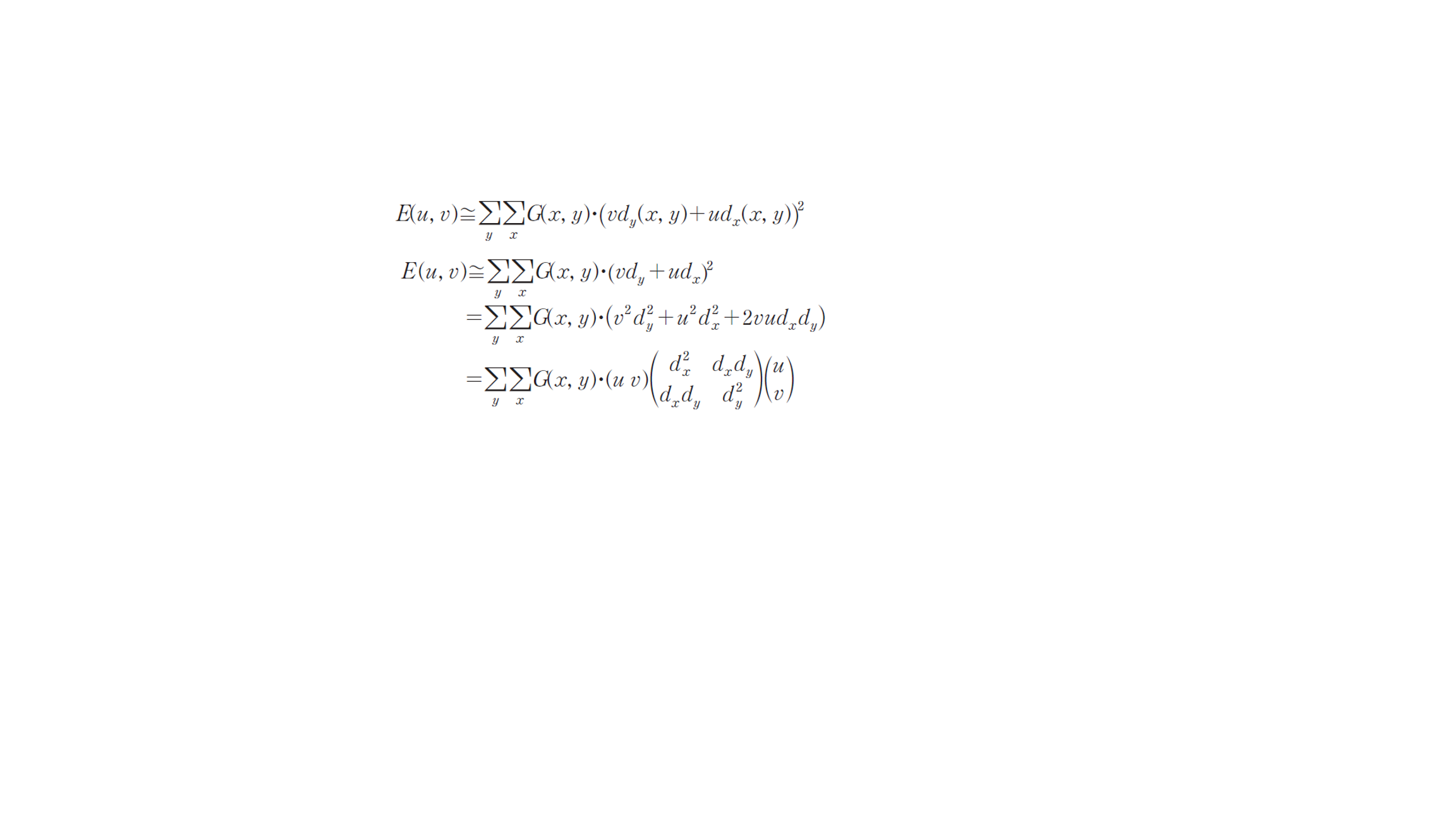
- 위 수식에서 중앙의 2x2 행렬을 M이라고 정의하면, 다음과 같이 다시 정리할 수 있다.
- 원래 함수 E(u, v)는 지역적 자기 상관 함수(local autocorrelation function)과 관련이 있으며, 행렬 M은 이 함수의 모양을 결정하는 행렬이다.
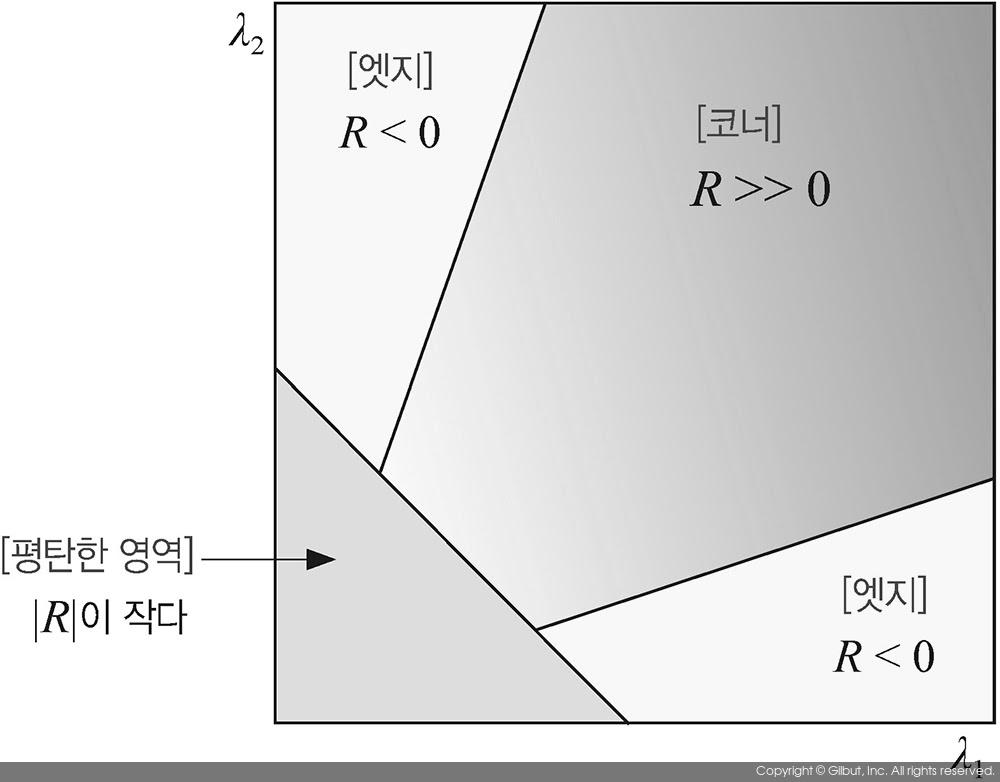
- 만약 행렬 M의 고윳값(eigenvalue)를 \(\lambda_1\), \(lambda_2\)라고 표현한다면, \(\lambda_1\)과 \(lambda_2\)의 값의 크기에 따라 해당 픽셀이 평탄한 영역인지 엣지, 혹은 코너 포인트 위치인지가 결정된다.
- \(\lambda_1\)과 \(lambda_2\)가 모두 작은 경우, 해당 점은 평탄한 영역에 속한 픽셀이다.
- \(\lambda_1\)과 \(lambda_2\) 중 하나는 큰 값, 다른 하나는 작은 값을 가지면 이는 엣지에 위치한 픽셀이다.
- \(\lambda_1\)과 \(lambda_2\)가 모두 큰 경우, 해당 점은 코너 포인트에 위치한 픽셀이다.
- 해리스 코너 포인트 검출 방법에서는 행렬 M의 고윳값을 직접 구하는 방법 대신 코너 응답 함수(corner response function)를 새롭게 정의하여 이 값을 코너 포인트를 찾는 척도로 사용한다.
- 위 수식에서 Det(M)은 행렬식이고, Tr(M)은 행렬 M의 대각합을 의미한다. 2x2 행렬 M에서 이 두 값은 고윳값 \(\lambda_1\), \(lambda_2\)에 대해 다음과 같은 성질을 만족한다.
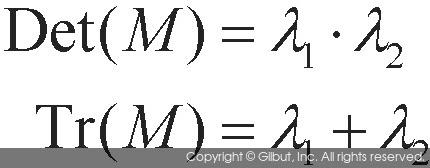
- 행렬의 고윳값을 직접 구하는 대신 행렬식과 대각합을 이용하여 고윳값의 곱과 합을 구할 수 있다. 코너 응답 함수 R의 값에 따라 평탄한 영역, 엣지 픽셀, 코너 픽셀로 구분한다.
- 모라벡(Moravec)의 방법
- 해리스 코너 검출 전체 과정 및 결과 1) 소벨 마스크로 미분 행렬 계산 (dx, dy) 2) 미분 행렬의 곱 계산 \((dx^2, dy^2, dxy)\) 3) 곱 행렬에 가우시안 마스크 적용 4) 코너 응답함수 \(C = Det(M) - Tr(M)^2\) 계산 5) 비최대치 억제
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void cornerharris(Mat image, Mat& corner, int bSize, int ksize, float k)
{
Mat dx, dy, dxy, dx2, dy2;
corner = Mat(image.size(), CV_32F, Scalar(0));
vector<int> a;
Sobel(image, dx, CV_32F, 1, 0, ksize);
Sobel(image, dy, CV_32F, 0, 1, ksize);
multiply(dx, dx, dx2);
multiply(dy, dy, dy2);
multiply(dx, dy, dxy);
// 미분 행렬 제곱
Size msize(5, 5);
GaussianBlur(dxy, dxy, msize, 0);
GaussianBlur(dx2, dx2, msize, 0);
GaussianBlur(dy2, dy2, msize, 0);
for (int i = 0; i < image.rows; i++) {
for (int j = 0; j < image.cols; j++)
{
float a = dx2.at<float>(i, j);
float b = dy2.at<float>(i, j);
float c = dxy.at<float>(i, j);
corner.at<float>(i, j) = (a * b - c * c) - k * (a + b) * (a + b);
}
}
}
Mat draw_coner(Mat corner, Mat image, int thresh)
{
int cnt = 0;
normalize(corner, corner, 0, 100, NORM_MINMAX, CV_32FC1, Mat());
for (int i = 1; i < corner.rows - 1; i++) {
for (int j = 1; j < corner.cols - 1; j++)
{
float cur = (int)corner.at<float>(i, j);
if (cur > thresh)
{
if (cur > corner.at<float>(i-1, j) &&
cur > corner.at<float>(i, j-1) &&
cur > corner.at<float>(i+1, j) &&
cur > corner.at<float>(i, j+1))
{
circle(image, Point(j, i), 2, Scalar(255, 0, 0), -1);
cnt++;
}
}
}
}
cout << "코너수: " << cnt << endl;
return image;
}
Mat image, corner1, corner2;
void cornerHarris_demo(int thresh, void*)
{
Mat img1 = draw_coner(corner1, image.clone(), thresh);
Mat img2 = draw_coner(corner2, image.clone(), thresh);
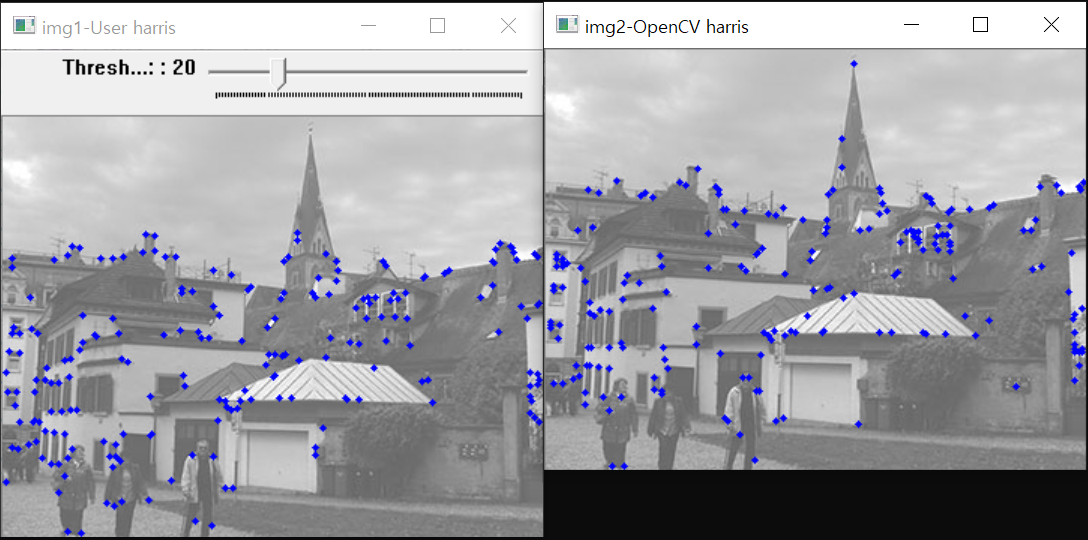
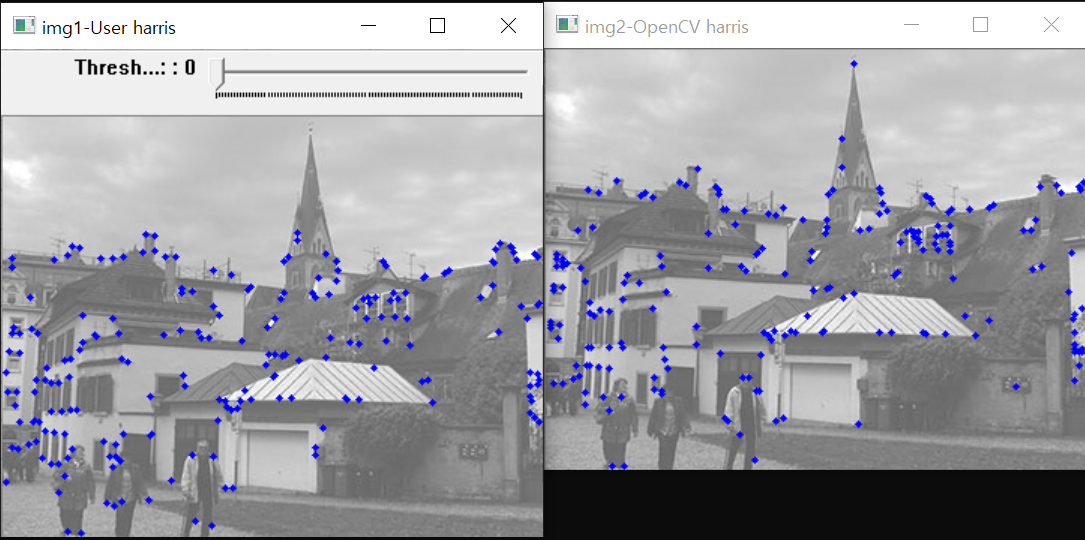
imshow("img1-User harris", img1);
imshow("img2-OpenCV harris", img2);
}
int main()
{
image = imread("../image/harris_test.jpg", 1); // 컬러 영상입력
CV_Assert(image.data);
int blockSize = 4;
int apertureSize = 3;
double k = 0.04;
int thresh = 20;
Mat gray;
cvtColor(image, gray, CV_BGR2GRAY);
cornerharris(gray, corner1, blockSize, apertureSize, k); // 직접 구현 함수
cornerHarris(gray, corner2, blockSize, apertureSize, k); // OpenCV 제공 함수
cornerHarris_demo(0, 0);
createTrackbar("Threshold: ", "img1-User harris", &thresh, 100, cornerHarris_demo);
waitKey();
}
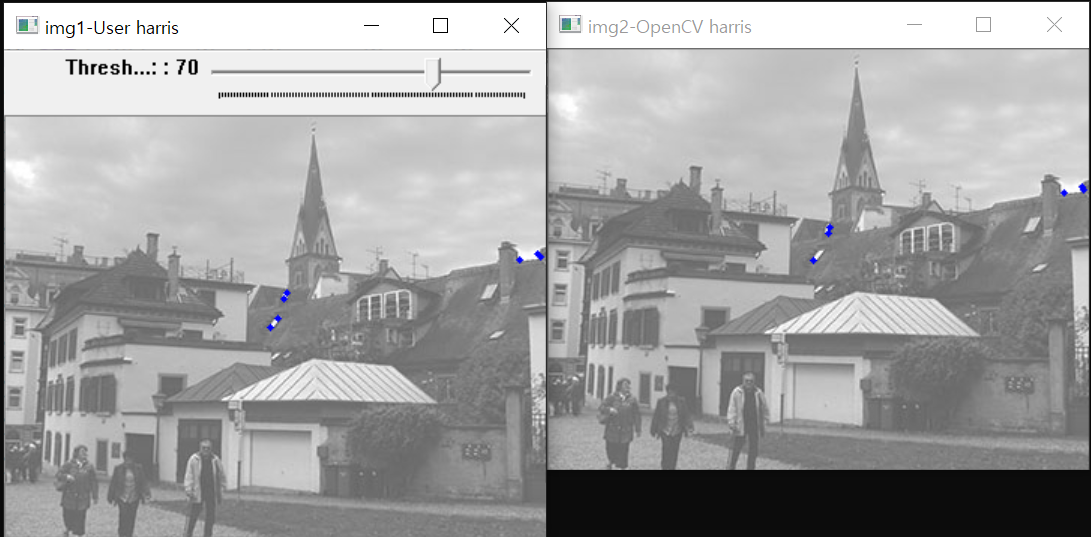
11.2.5. K-최근접 이웃 분류기의 이해
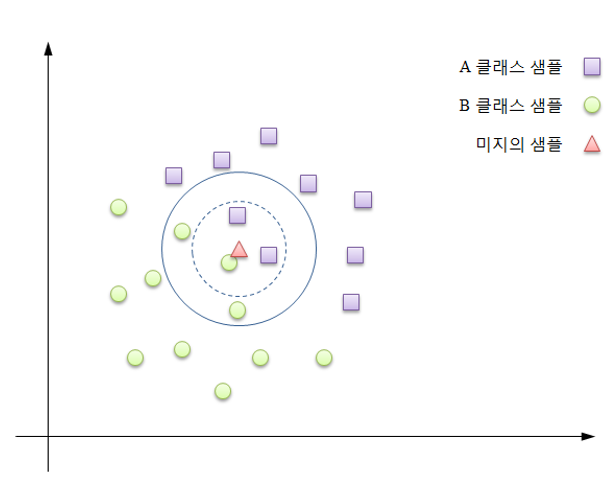
- 최근접 이웃 알고리즘
- 기존에 가지고 있는 데이터들을 일정한 규칙에 의해 분류된 상태에서 새로운 입력 데이터의 종류를 예측하는 분류 알고리즘
- 장점
- 단순하고 효율적이다.
- 기저 데이터 분포에 대한 가정을 하지 않는다. = 비모수이고, 분포에 대한 가정이 없다.
- 훈련 단계가 빠르다.
- 어떤 데이터가 주어져도 해당 사례에 대한 유사성을 측정할 수 있다.
- 단점
- 대용량 데이터에 대한 계산 효율성이 매우 떨어진다.
- 성능이 차원에 달려있다.
- 모델을 생성하지 않아 특징과 클래스간의 관계를 이해하는 능력이 제약된다.
- 적절한 k의 선택이 필요하다.
- 분류 단계가 느리다.
- k는 최근접 이웃의 개수를 임의로 사용해도 된다는 것을 의미하는 변수 항목이며, k가 선택된 이후 알고리즘은 여러 범주로 분류되어 명목 변수로 레이블된 예시들로 구성된 훈련 데이터셋을 필요로 한다.
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void make_tranData(Mat trainData, Mat group[2], Mat& classLable)
{
int half = trainData.rows / 2;
Range r1(0, half);
Range r2(half, trainData.rows);
group[0] = trainData.rowRange(r1);
group[1] = trainData.rowRange(r2);
randn(group[0], 150, 50);
randn(group[1], 250, 50);
classLable.rowRange(r1).setTo(0);
classLable.rowRange(r2).setTo(1);
}
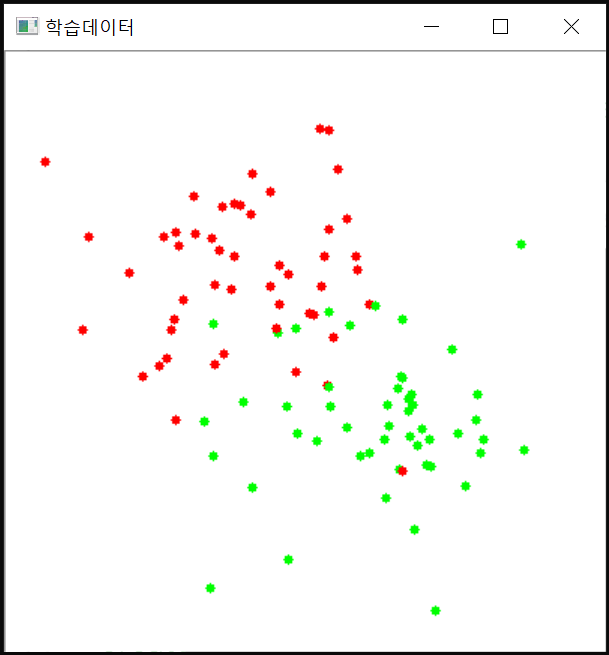
// group[0]은 빨간색 원(윗쪽)
// group[1]은 초록색 원(아랫쪽)
void draw_points(Mat& image, Mat group[2])
{
for (int i = 0; i < group[0].rows; i++)
{
Point2f pt1(group[0].at<float>(i, 0), group[0].at<float>(i, 1)); // 윗부분 (x, y)
Point2f pt2(group[1].at<float>(i, 0), group[1].at<float>(i, 1)); // 아랫부분 (x, y)
circle(image, pt1, 3, Scalar(0, 0, 255), FILLED);
circle(image, pt2, 3, Scalar(0, 255, 0), FILLED);
}
}
int main()
{
int Nsample = 100;
Mat trainData(Nsample, 2, CV_32FC1, Scalar(0));
Mat classLable(Nsample, 1, CV_32FC1, Scalar(0));
Mat image(400, 400, CV_8UC3, Scalar(255, 255, 255));
Mat group[2];
make_tranData(trainData, group, classLable);
draw_points(image, group);
imshow("학습데이터", image);
waitKey();
return 0;
}
// KNearst 클래스
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
void make_trainData(Mat trainData, Mat group[2], Mat& classLable)
{
int half = trainData.rows / 2;
Range r1(0, half);
Range r2(half, trainData.rows);
group[0] = trainData.rowRange(r1);
group[1] = trainData.rowRange(r2);
randn(group[0], 150, 50);
randn(group[1], 250, 50);
classLable.rowRange(r1).setTo(0);
classLable.rowRange(r2).setTo(1);
}
void draw_points(Mat& image, Mat group[2])
{
for (int i = 0; i < group[0].rows; i++)
{
Point2f pt1(group[0].at<float>(i, 0), group[0].at<float>(i, 1));
Point2f pt2(group[1].at<float>(i, 0), group[1].at<float>(i, 1));
circle(image, pt1, 3, Scalar(0, 0, 255), FILLED);
circle(image, pt2, 3, Scalar(0, 255, 0), FILLED);
}
}
void kNN_test(Ptr<ml::KNearest> knn, int K, Mat& image)
{
for (int y = 0; y < image.rows; y++) {
for (int x = 0; x < image.cols; x++)
{
Matx12f sample((float)x, (float)y);
Mat response;
knn->findNearest(sample, K, response); // 분류 수행
int resp = (int)response.at<float>(0);
if (resp == 1) image.at<Vec3b>(y, x) = Vec3b(0, 180, 0);
else image.at<Vec3b>(y, x) = Vec3b(0, 0, 180);
}
}
}
int main()
{
int Nsample = 100;
Mat trainData(Nsample, 2, CV_32FC1, Scalar(0));
Mat classLable(Nsample, 1, CV_32FC1, Scalar(0));
Mat group[2];
make_trainData(trainData, group, classLable);
Mat image(400, 400, CV_8UC3, Scalar(255, 255, 255));
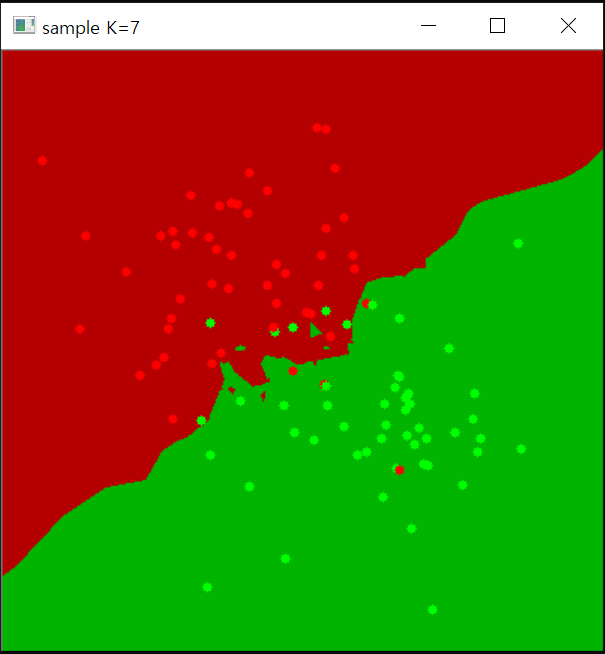
int K = 7;
Ptr<ml::KNearest> knn = ml::KNearest::create();
knn->train(trainData, ml::ROW_SAMPLE, classLable);
kNN_test(knn, K, image);
draw_points(image, group);
imshow("sample K=" + to_string(K), image);
waitKey();
return 0;
}
11.2.6. K-NN으로 숫자 분류하기 실습
#include "kNN.hpp"
int main()
{
Size size(40, 40); // 학습 셀 크기
int K = 15; // 선출하는 이웃 샘플수
int Nclass = 10; // 인식 숫자(카테고리) 개수
int Nsample = 20; // 숫자당 학습 샘플수
string image_file = "../image/train_numbers.png";
Mat train_image = imread(image_file, 0); // 영상 로드
CV_Assert(train_image.data);
threshold(train_image, train_image, 32, 255, CV_THRESH_BINARY);
Mat trainData, classLable;
for (int i = 0, k = 0; i < Nclass; i++) {
for (int j = 0; j < Nsample; j++, k++)
{
Point start(j * size.width, i * size.height);
Rect roi(start, size);
Mat part = train_image(roi); // 숫자 영상 분리
Mat num = find_number(part); // 숫자 영역 영상
Mat data = place_middle(num, size); // 정규화 및 1행데이터 구성
trainData.push_back(data); // 학습 데이터 수집
classLable.push_back(i); // 레이블링
}
}
Ptr<ml::KNearest> knn = ml::KNearest::create();
knn->train(trainData, ml::ROW_SAMPLE, classLable); // k-NN 학습
int no;
cout << "영상번호를 입력하세요: ";
cin >> no; // 영상번호 입력
string demo_file = format("../image/num/%02d.png", no);
Mat test_img = imread(demo_file, 0); // 실험 영상 로드
CV_Assert(test_img.data); // 예외처리
threshold(test_img, test_img, 128, 255, THRESH_BINARY); // 이진화
Mat num = find_number(test_img); // 숫자객체 검출
Mat data = place_middle(num, size); // 숫자객체 셀 중심 배치
Mat result;
knn->findNearest(data, K, result); // 숫자 분류 수행
cout << "분류결과 : " << result.at<float>(0) << endl;
imshow("test_img", test_img);
waitKey();
return 0;
}
11.2.7. 영상 워핑과 영상 모핑
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
Point2f pt1, pt2;
Mat image;
void morphing()
{
Mat dst(image.size(), image.type(), Scalar(0));
int width = image.cols;
int height = image.rows;
for (float y = 0; y < image.rows; y += 0.1f) {
for (float x = 0; x < image.cols; x += 1) // x가 0.1인 이유는 값이 너무 크면 홀이 생겨버리기 때문에
{
float ratio;
if (y < pt1.y) {
ratio = y / pt1.y;
}
else {
ratio = (height - y) / (height - pt1.y);
}
/*
if (x < pt1.x) {
ratio = x / pt1.x;
}
else {
ratio = (width - x) / (width - pt1.x);
}
float dx = ratio * (pt2.x - pt1.x);
float dy = ratio * (pt2.y - pt1.y);
dst.at<uchar>(y, x + dx) = image.at<uchar>(y, x); // 역방향 사상
// dst.at<uchar>(y + dy, x) = image.at<uchar>(y, x); // 역방향 사상
}
}
dst.copyTo(image);
imshow("image", image);
}
void onMouse(int event, int x, int y, int flags, void* param)
{
if (event == EVENT_LBUTTONDOWN) {
pt1 = Point2f(x, y);
}
else if (event == EVENT_LBUTTONUP) {
pt2 = Point2f(x, y);
morphing();
}
}
int main()
{
image = imread("../image/warp_test.jpg", 0);
CV_Assert(image.data);
imshow("image", image);
setMouseCallback("image", onMouse);
waitKey();
return 0;
}