선형대수학
챕터1: 벡터, 행렬, 행렬식
1.1. 벡터와 공간
1.1.1. 벡터(vector)
수치의 조합을 정리하여 나타내는 기법이다. 수를 나열한 것으로, 성분수를 명시하고 싶을 때는 \(\begin{pmatrix} 3 \\ 0 \end{pmatrix}\) \(\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\) 각각 2차원 벡터, 3차원 벡터로 불린다.
1.1.2. 공간(space)
2차원 벡터는 \(x, y\)축으로 이루어지는 좌표에 점으로 찍을 수 있으며, 3차원 벡터는 \(x, y, z\)축으로 이루어진 좌표에 점을 찍을 수 있다. 이런 식으로 벡터들은 공간에 대응시킬 수 있다.
1.1.3. span
동사로 ‘포괄하다’, ‘걸치다’, ‘가로지르다’의 의미를 가지며, 일반적으로 “span a space” 라고 하는데 “어떤 공간을 포괄하다”라는 의미이다.
- 두 개의 벡터 \(v_1\) = [2, 3], \(v_2\) = [3, 2]가 있다고 가정하자. \(v_1\)과 \(v_2\)가 어떤 공간을 포괄한다고 할 때, 이것이 의미하는 것은?
span이라는 것은 이 벡터들로 형성할 수 있는 공간을 의미한다. 즉, 선형 조합을 통해 만들어지는 공간이다.
1.1.4. 기저(bias)
특정 벡터 \(\overrightarrow{v}\)를 지정하는데, ‘여기’라고 손가락으로 가리키는 것 보다 말로도 위치를 전달할 수 있도록 ‘번지(좌표)’를 매겨주자. 아래의 그림과 같은 기준이 되는 벡터 \(\overrightarrow{e_1}\), \(\overrightarrow{e_2}\)를 정한다.
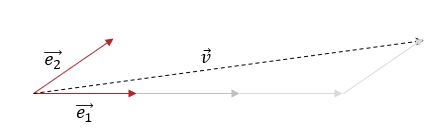
기준을 정하면 ”\(\overrightarrow{e_1}\) 을 3칸, \(\overrightarrow{e_2}\) 를 2칸” 처럼 말하여 벡터 \(\overrightarrow{v}\)의 위치를 지정할 수 있다.
기저는 어떤 공간을 span하면서 독립인 벡터들이라 할 수 있다.
- 기저는 2가지의 성질을 가지고 있다.
기저 벡터들은 서로 독립이다.
기저 벡터들은 공간을 span 한다.
- 3차원 공간 \(R^3\)에 대한 기저는 무엇일까? 즉, 독립이면서 3차원 공간을 span하는 벡터는 무엇일까?
가장 쉽게 떠올릴 수 있는 벡터는 바로, \(e_1\) = [1, 0, 0], \(e_2\) = [0, 1, 0], \(e_3\) = [0, 0, 1] 이다.
이들 벡터는 서로 독립이면서, 직관적으로 생각해보면 각각 \(x\)축, \(y\)축, \(z\)축을 나타낸다.
위의 형태를 표준 기저라 하며, 기저를 표현할 수 있는 벡터는 무수히 많다.
1.1.5. 차원(dimension)
\(n\)차원이면 기저 벡터는 \(n\)개이다. 즉, 차원은 기저 벡터의 개수라 할 수 있다.
1.2. 행렬과 사상
1.2.1. 행렬은 사상이다
\(n\)차원 벡터 \(x\)에 \(m \times n\) 행렬 \(A\)를 곱하면 \(m\)차원 벡터 \(y = Ax\)가 얻어진다. 즉, 행렬 \(A\)를 지정하면 벡터를 다른 벡터에 옮기는 사상이 결정된다. 행렬을 단순히 “수가 나열되어 있다”로 보지말고, “사상되어 있다”로 보자.
1.2.2. 행렬의 곱은 사상의 합이다
\(A, B\)를 각각 \(m \times n, n \times p\) 행렬이라고 하자. \(A\)와 \(B\)의 곱 \(AB\)는 다음과 같은 항을 갖는 \(m \times p\) 행렬로 정의된다.
\({\displaystyle (\mathbf {AB} )_{ij}=A_{i1}B_{1j}+A_{i2}B_{2j}+\cdots +A_{in}B_{nj}=\sum _{k=1}^{n}A_{ik}B_{kj}}{\displaystyle (\mathbf {AB} )_{ij}=A_{i1}B_{1j}+A_{i2}B_{2j}+\cdots +A_{in}B_{nj}=\sum _{k=1}^{n}A_{ik}B_{kj}}\)
즉, \({\displaystyle \mathbf {AB} ={\begin{pmatrix}\sum _{k=1}^{n}A_{1k}B_{k1}&\sum _{k=1}^{n}A_{1k}B_{k2}&\cdots &\sum _{k=1}^{n}A_{1k}B_{kp}\\\sum _{k=1}^{n}A_{2k}B_{k1}&\sum _{k=1}^{n}A_{2k}B_{k2}&\cdots &\sum _{k=1}^{n}A_{2k}B_{kp}\\\vdots &\vdots &&\vdots \\\sum _{k=1}^{n}A_{mk}B_{k1}&\sum _{k=1}^{n}A_{mk}B_{k2}&\cdots &\sum _{k=1}^{n}A_{mk}B_{kp}\end{pmatrix}}}\)
좌측 행렬의 열 수와 우측 행렬의 행 수가 서로 같아야, 두 행렬의 곱이 정의된다.[위키백과]
세 행렬 \(A, B, C\)의 곱을 살펴보자.
- ’\(A\)하고, \(B\)한다’를 하고 나서 \(C\)를 한다.
- \(A\)를 하고 나서 ‘\(B\)하고, \(C\)한다’를 한다.
위의 표현을 식으로 나타내면 \(C(BA) = (CB)A\)와 같다. 이렇듯, 행렬의 곱은 결합법칙이 성립한다.
두 행렬 \(A, B\)의 곱을 살펴보자. 행렬 \({\displaystyle A={\begin{bmatrix}a\\b\end{bmatrix}}}\)와 \({\displaystyle B={\begin{bmatrix}c&d\end{bmatrix}}}\)가 있을 때, 이 둘의 곱셈은 다음과 같다.
\({\displaystyle A\times B={\begin{bmatrix}a\\b\end{bmatrix}}\times {\begin{bmatrix}c&d\end{bmatrix}}={\begin{bmatrix}ac&ad\\bc&bd\end{bmatrix}}}\)
\({\displaystyle B\times A={\begin{bmatrix}c&d\end{bmatrix}}\times {\begin{bmatrix}a\\b\end{bmatrix}}=ca+db}\)
위의 표현을 식으로 나타내면 \(AB \neq BA\)로, 행렬의 곱은 교환법칙이 성립하지 않는다.
1.2.3. 행렬 연산의 성질
- \((cA)x = c(Ax) = A(cx)\)
- \((A + B)x = Ax + Bx\)
- \(A + B = B + A\)
- \((A + B) + C = A + (B + C)\)
- \((c + c')A = cA + c'A\)
- \((cc')A = c(c'A)\)
- \(A(B + C) = AB + AC\)
- \((A + B)C = AC + BC\)
- \((cA)B = c(AB) = A(cB)\)
1.2.4. 행렬의 거듭제곱은 사상의 반복이다
정방행렬 \(A\)에 대해 \(AA = A^2, AAA = A^3\)은 사상으로서 ‘\(A\)하고 한층 더 \(A\)한다’, ‘\(A\)하고 \(A\)하고 \(A\)한다’이다. 즉, \(A^n\)은 ‘\(A\)를 \(n\)번 반복 적용한다’이다.
1.2.5. 영행렬, 단위행렬, 대각행렬
- 영행렬: 모든 성분이 \(0\)인 행렬로, 모든 것을 원점으로 이동시키는 사상이다.
- 단위행렬: \(\setminus\) 방향의 대각선 위만 1이고, 나머지는 모두 \(0\)인 행렬로, 아무것도 하지 않는 사상이다.
- 대각행렬: \(\setminus\) 방향의 대각선상의 값을 대각성분이라 하고 나머지 값을 비대각성분이라 하는데, 비대각성분이 모두 \(0\)인 행렬이다. 대각행렬은 축에 따르는 신축(늘고 줄음)이고, 대각성분이 각 축의 늘고 주는 배율이 되는 사상이다.