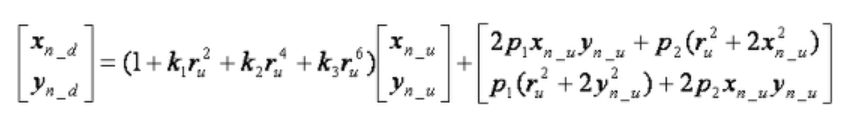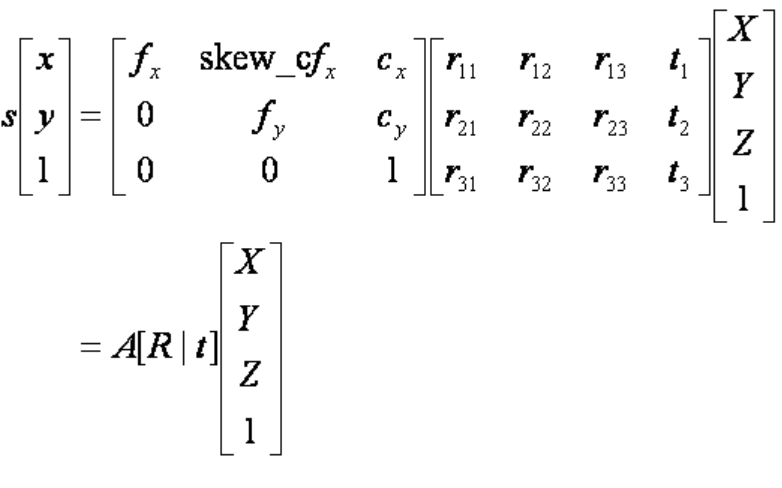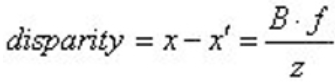Mobile Robotics and ROS [Day 4]

Published On June 20, 2020

다크 프로그래머

Perception ~ Visual Perception

Vision for Robotics
Camera Model
Perspective Projection
Camera Calibration
Distance Measure with Camera
Image Processing

1. Vision for Robotics

카메라: 캡처된 상을 디지털 이미지로 변환
다양한 분야에서 사용가능한 어플리케이션

2. Camera Model

Pinhole Camera Model
- geometry 측정을 위한 카메라
- 핀홀에 있는 구멍에만 특정 물체의 빛이 투과됨
- 역상으로 맺힘
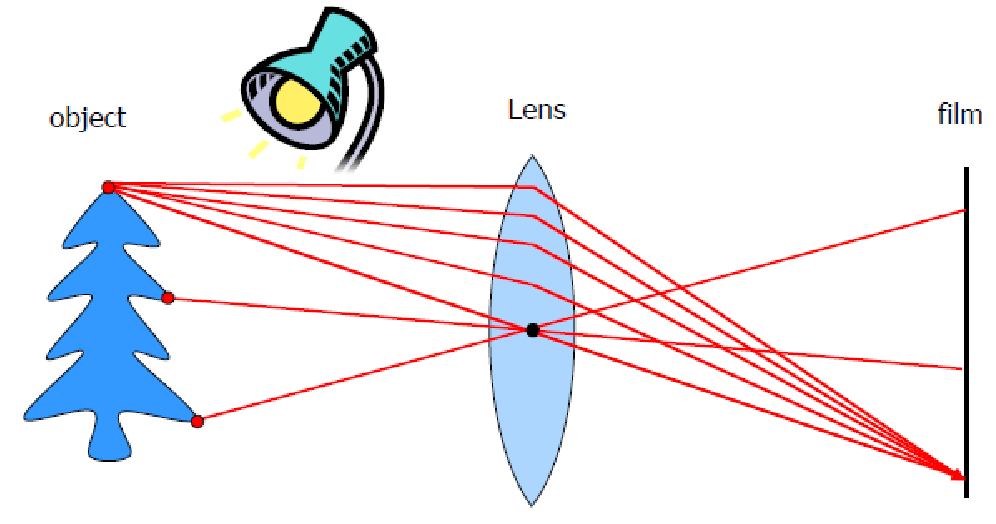
- 필름에 투과되는 중심점을 Optical Center, 상이 맺혀지는 뒷면을 Image Plane
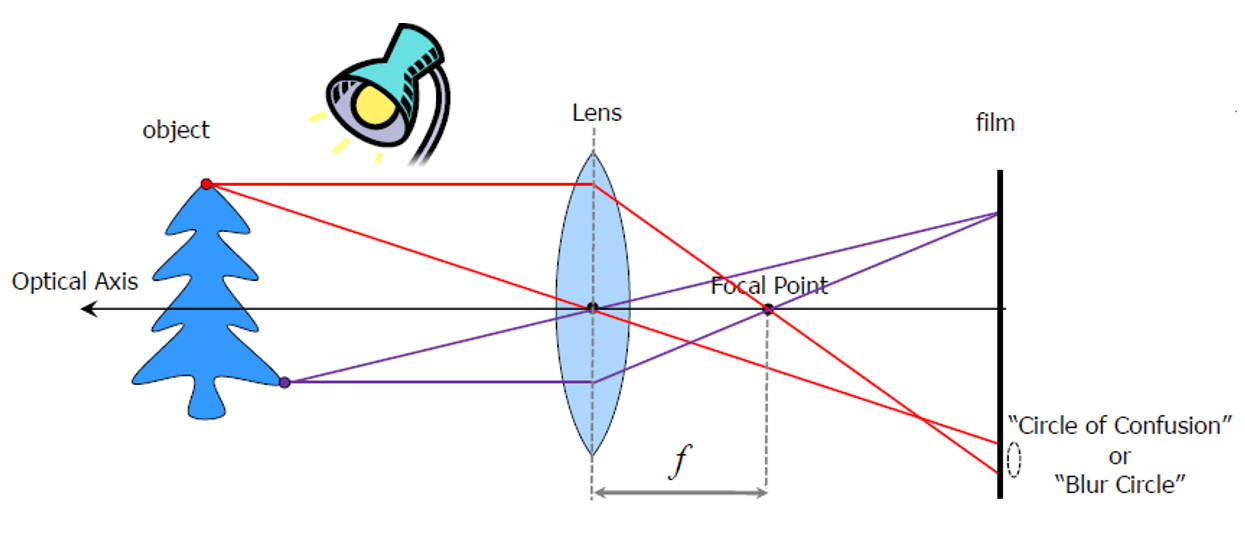
- 핀홀이 작을수록 투과되는 빛의 양이 줄어들 수밖에 없어서 흐릿해짐 » 렌즈를 사용하면 빛을 모아서 한 점에 맺히도록(볼록렌즈) -> 밝고 선명한 영상을 얻을 수 있음
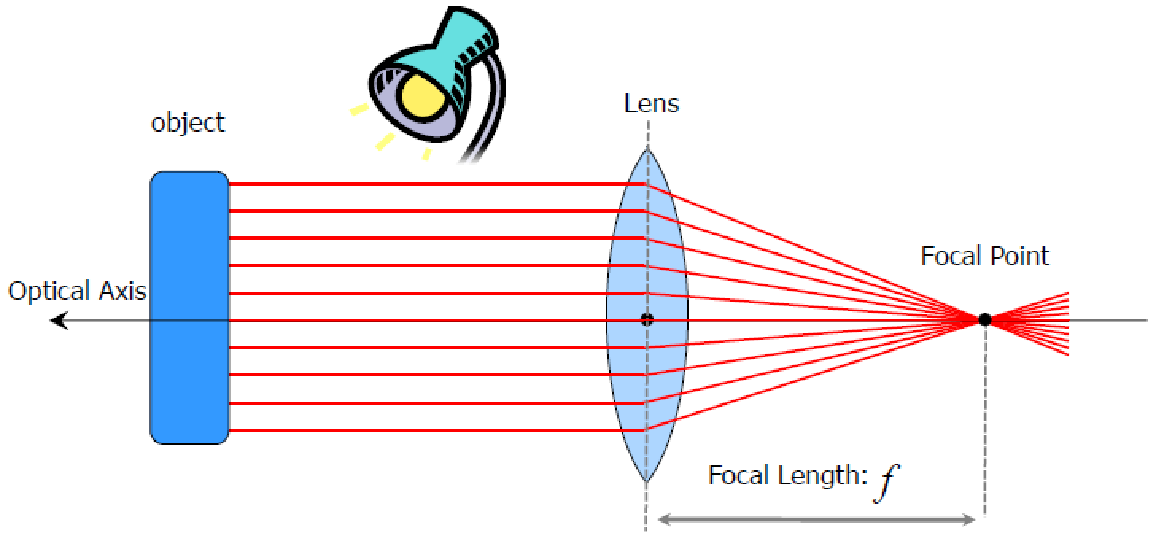
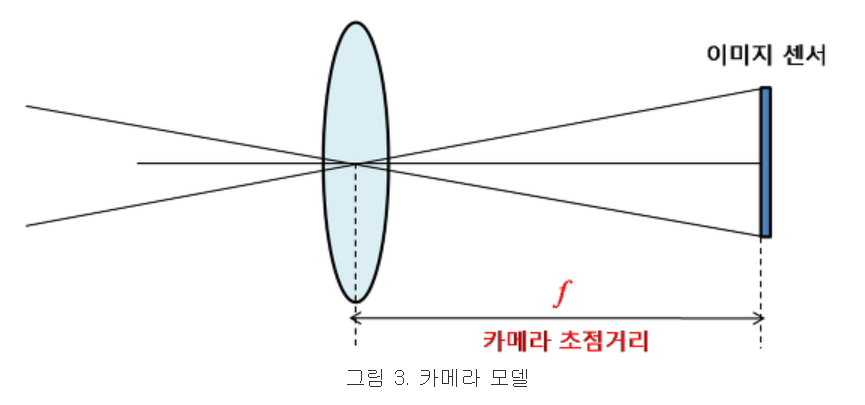
- 초점이 모아지는 부분을 Focal Point
- 렌즈와 Focal Point 사이의 거리를 Focal Length
- 렌즈와 물체간의 평행한 축을 Optical Axis

3. Perspective Projection

레이를 따라서 한 점들이 모여서 만들어짐
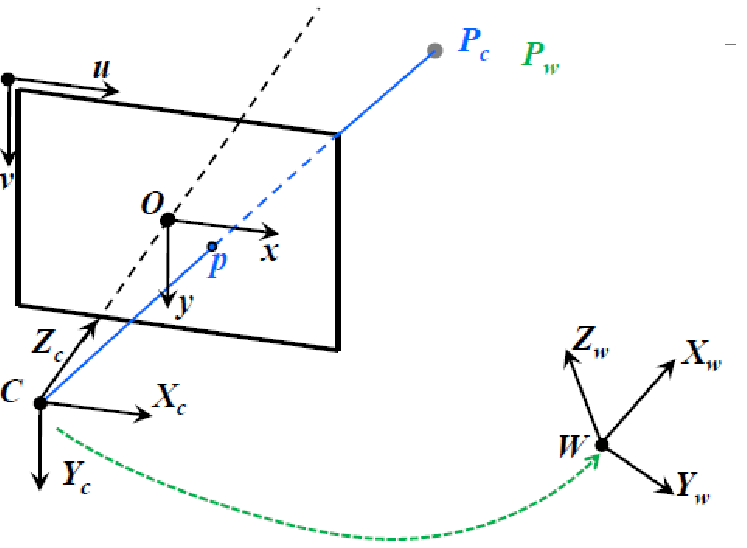
3차원의 공간의 점들이 2차원 점들에 닿으면서 COP(Center of Projection)로 도달하는데, 이 때 2차원들의 집합이 Projection Plane임
Perspective Camera
- COP를 기준으로 3차원 좌표계가 형성
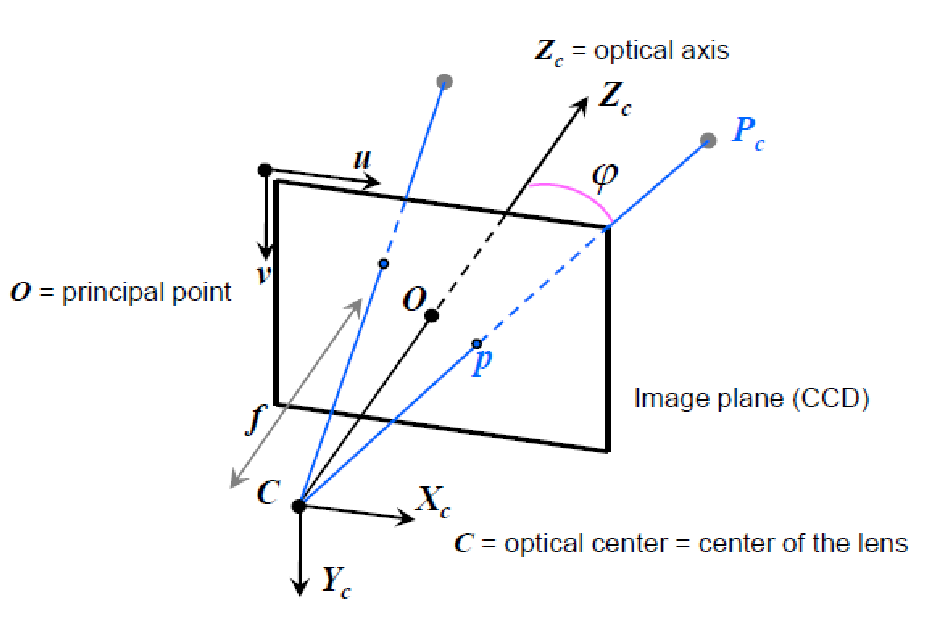
- CCD, CMOS 센서가 놓여있는 위치가 Image Plane(무한대가 아닌 한정된 영역)
- 가장 좌측 위쪽을 Image Plane의 COP라 한다.
- Optical axis와 Image Plane과 만나는 점이 Principal point라 한다.
- 카메라는 거리를 측정할 수 없지만, 앵글은 측정 가능(bearing sensor) -> 3차원에서 2차원으로 줄어들기 때문에 거리 계산은 불가능하지만, ray들과 COP가 주어지므로, 각도를 구할 수 있다.
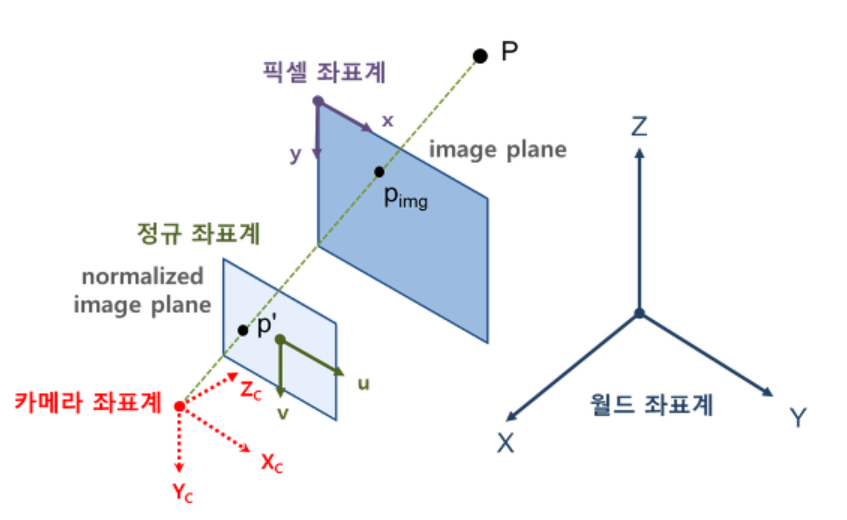
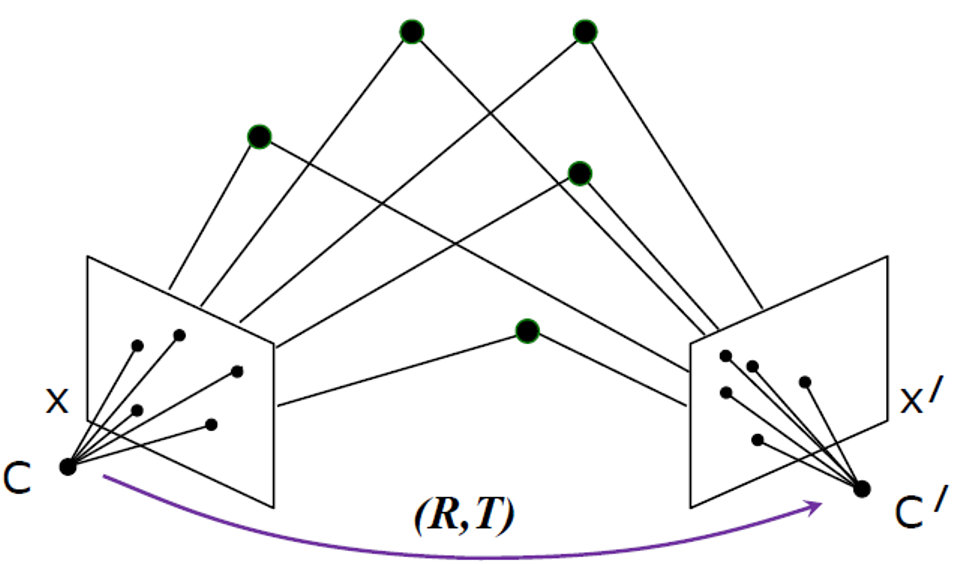
World to Pixel coordinates
- frame 간에 상관관계를 알면, world point와 기준 포인트 간의 거리를 알 수 있음
- Rotation / Translation
- \(P_w -> P_c\)(점이 바뀌는 것이 아니라(점은 그대로 있음), 표현하는 방식이 카메라 프레임으로 바뀌는 것)
- \(P_w\)가 Image plane의 (u, v)로 픽셀 점으로 변환이 가능
- Homogeneous Coordinates(동차 좌표계)
  - (x, y)를 (x, y, 1)로 표현하는 것이다. 좀 더 일반적으로 임의의 상수 w에 대해 (x, y)를 (wx, wy, w)로 표현한 것이다.
  - 역으로 동차 좌표계에서 원래의 좌표를 구하려면 끝자리가 1이 되도록 scale을 바꾼 후 1을 빼면 된다. 즉, \((x, y, \alpha)\)는 \((x/\alpha, y/\alpha, 1)\)과 같으며, 실제 2D 좌표는 \((x/\alpha, y/\alpha)\)와 같다.
  - 동차 좌표계를 사용하는 이유는 perspective 변환을 하나의 단일 행렬로 표현할 수 있기 때문이다.
- 각 필요한 변수를 구하는 과정을 Camera Calibration
- 호모지니어스 matrix - 1을 넣어줘서 하나의 매트릭스로 표현 가능
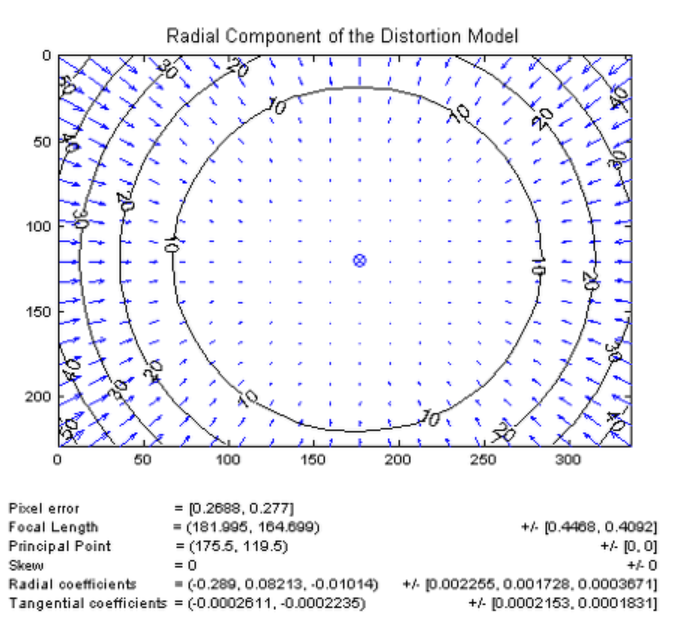
Radial distortion(방사형 왜곡)
- 렌즈를 사용하다보면 왜곡이 발생 가능(가장 자리로 갈 수록 곡률에 의해 영상이 왜곡)하다. 이러한 영상 왜곡은 시각적인 문제외에도 영상분석을 통해서 정확한 수치 계산이 필요할 때 문제가 된다.
- 예를 들어, 영상에서 검출한 물체의 실제 위치를 알기 위해 영상좌표를 물리적인 좌표로 변환한다면 영상왜곡 정도에 따라 심각한 오차가 발생할 것이다.
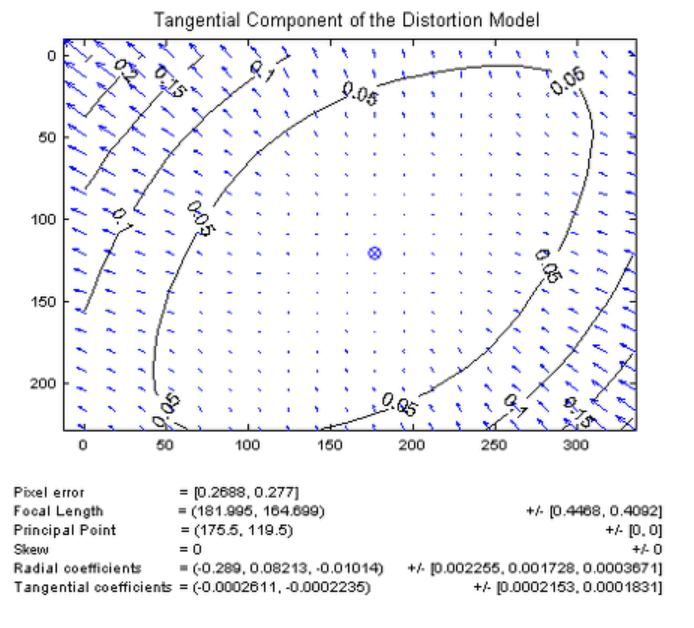
- 렌즈 왜곡에는 크게 방사 왜곡(radial distortion)과 접선 왜곡(tangential distortion)이 있다.
- 방사 왜곡은 볼록렌즈의 굴절률에 의한 것으로 영상의 왜곡 정도가 중심에서 거리에 의해 결정되는 왜곡이다.
- 접선 왜곡은 카메라 제조과정에서 카메라 렌즈와 이미지 센서(CCD, CMOS)의 수평이 맞지 않거나 또는 렌즈 자체의 centering이 맞지 않아서 발생하는 왜곡으로 타원형 형태로 왜곡 분포가 달라진다.
- 렌즈계의 왜곡 모델은 다음과 같으며, 우변의 첫 번째 항은 방사 왜곡, 두 번째 항은 접선 왜곡을 나타낸다.
- \(k_1, k_2, k_3\)는 방사 왜곡의 계수, \(p_1, p_2\)는 접선 왜곡의 계수이며, \(r_u\)는 왜곡이 없을 때의 중심까지의 거리(반지름)이다.

4. Camera Calibration

카메라 캘리브레이션이란?
- 우리가 실제 눈으로 보는 세상은 3차원이지만, 카메라로 찍으면 2차원이 된다. 이 때, 3차원의 점들이 이미지 상에서 어디에 맺히는지는 기하학적으로 생각하면, 영상을 찍을 당시의 카메라의 위치 및 방향에 의해 결정된다.
- 하지만, 실제 이미지는 사용된 렌즈, 렌즈와 이미지 센서와의 거리, 렌즈와 이미지 센서가 이루는 각 등 카메라 내부의 기구적인 부분에 의해 크게 영향을 받는다.
- 따라서, 3차원 점들이 영상에 투영된 위치를 구하거나 역으로 영상좌표로부터 3차원 공간좌표를 복원할 때에는 이러한 내부 요인을 제거해야 한다. 이러한 내부 요인의 파라미터 값을 구하는 과정을 카메라 캘리브레이션이라고 한다.

캘리브레이션의 개요

카메라 영상은 3차원 공간상의 점들을 2차원 이미지 평면에 투사(perspective projection)함으로써 얻어진다.
핀홀 카메라 모델에서 이러한 변환 관계는 다음과 같다.

(X, Y, Z)는 월드 좌표계 상의 3D 점의 좌표, [R

t]는 월드 좌표계를 카메라 좌표계로 변환시키기 위한 회전/이동변환 행렬이며, A는 intrinsic camera matrix이다.

수직적으로 보면 캘리브레이션은 위와 같은 3차원 공간좌표와 2차원 영상좌표 사이의 변환관계 또는 변환관계를 설명하는 파라미터를 찾는 과정이다.

위의 수식에서 [R

t]를 카메라 외부 파라미터, A를 내부 파라미터라고 하며, 둘을 합쳐서 camera matrix 또는 projection matrix라고 한다.

카메라 내부 파라미터(Intrinsic Parameters)
- 초점거리(focal length)
  - 렌즈중심과 이미지센서(CCD, CMOS)와의 거리
  - 디지털 카메라 등에서 초점거리는 mm단위로 표현되지만, 카메라 모델에서의 초점거리(f)는 픽셀 단위로 표현된다.
  - 이미지의 픽셀은 이미지 센서의 셀에 대응되기 때문에, 초점거리(f)가 픽셀 단위라는 의미는 초점거리가 이미지 센서의 셀 크기에 대한 상대적인 값으로 표현된다는 의미이다.
  - 픽셀 단위로 표현하는 이유는 이미지 픽셀과 동일한 단위로 초점거리를 표현함으로써 영상에서의 기하학적 해석을 용이하게 하기 위함이다.
  - 카메라 모델에서 초점거리를 하나의 값으로 f라 표현하지 않고, 이미지 센서의 물리적인 셀 간격이 가로 방향과 세로 방향이 서로 다를 수 있기에 \(f_x, f_y\)로 구분하여 표현한다.
  - 카메라 모델의 렌즈중심(초점)은 핀홀 카메라 모델에서 핀홀(pinhole)에 해당한다. 핀홀 카메라 모델은 모든 빛은 한 점(초점)을 직선으로 통과하여 이미지 평면에 투영된다는 모델이다. 이러한 핀홀 모델은 3D 공간과 2D 이미지 평면 사이의 기하학적 투영 관계를 단순화시켜준다.
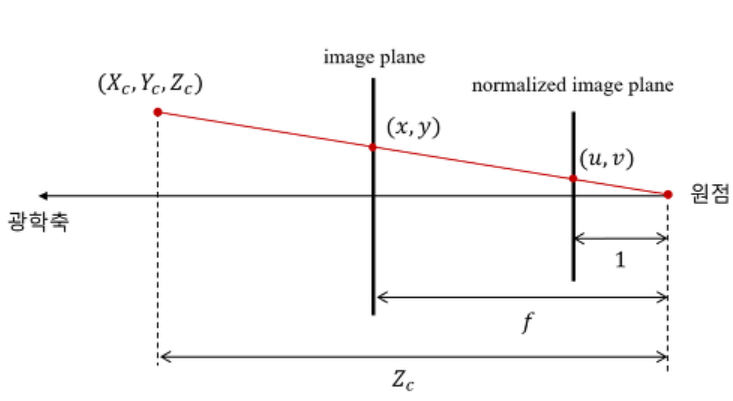
  - 초점으로부터 거리가 1인 평면을 normalized image plane이라고 부르며, 이 평면상의 좌표를 가상의 이미지 평면인 normalized image coordinate라고 한다.
  - 카메라 좌표계 상의 한 점 \((X_c, Y_c, Z_c)\)를 영상좌표계로 변환할 때, 먼저 \((X_c, Y_c)\)를 \(Z_c\)(카메라 초점에서의 거리)로 나누는 것은 normalized image plane 상의 좌표로 변환하는 것이며, 여기에 다시 초점거리 f를 곱하면 원하는 이미지 평면에서의 영상좌표(pixel)이 나온다. 그러나 이미지에서 픽셀좌표는 이미지의 중심이 아닌 이미지의 좌상단 모서리를 기준으로 하기 때문에 실제 최종적인 영상좌표는 여기에 \((c_x, c_y)\)를 더한 값이 된다.
- 주점(principal point)
  - 주점 \((c_x, c_y)\)는 카메라 렌즈의 중심, 즉 핀홀에서 이미지 센서에 내린 수선의 발의 영상좌표로서 일반적으로 말하는 영상 중심점과는 다른 의미이다.
  - 예를 들어, 카메라 조립과정에서 오차로 인해 렌즈와 이미지 센서가 수평이 어긋나면 주점과 영상중심은 다른 값을 가질 것이다.
  - 영상기하학에서는 단순한 이미지 중심점보다는 주점이 훨씬 중요하다.
- 비대칭 계수(skew coefficient)
  - 비대칭 계수는 이미지 센서의 cell array의 y축이 기울어진 정도이다.
카메라 외부 파라미터(Extrinsic Parameters)
- 카메라 좌표계와 월드 좌표계 사이의 변환 관계를 설명하는 파라미터로서, 두 좌표계 사이의 회전 및 평행이동 변환으로 표현된다.
- 카메라 외부 파라미터는 카메라 고유의 파라미터가 아니기 때문에 카메라를 어떤 위치에 어떤 방향으로 설치했는지에 따라 달라지고, 월드 좌표계를 어떻게 정의했느냐에 따라서 달라진다.

5. Distance Measure with Camera

거리 정보를 측정
- 하나의 점을 가지고는 거리 측정이 어려움
  => 카메라를 2대 이상 사용
  => 카메라 사이의 거리차를 이용(Stereo Vision)
- 예를 들어, 공을 던졌다 잡을 때 한쪽 눈을 감고 던졌다 잡으려고 하면 공과 거리감이 사라져 잡기가 어려워진다. 사라진 거리 정보를 복원하기 위해서는 또 다른 위치에서 찍은 다른 사진이 필요하다. 때문에 사람의 눈도 2개가 있어 물체를 서로 다른 장소(양쪽 각각의 눈 위치)에서 보고, 그 영상의 차이를 이용해 거리를 복원한다.
- 이처럼 “같은 물체에 대해 서로 다른 장소에서 촬영한 여러 이미지에서 물체의 3차원 정보를 계산하는 학문 분야”가 스테레오 비전이다.
Stereo Vision
- 3차원 거리 정보는 시차(disparity), 초점거리(focal length), 베이스라인(baseline)을 통해 획득이 가능하다.
- disparity는 좌/우 영상에서 동일하게 나타나는 물체에 대한 x축 위치 차이를 의미한다.
- 초점거리는 이미지 평면(CCD, CMOS)와 카메라 렌즈와의 거리이다.
- 베이스라인은 좌/우 카메라의 간격이다.
- 거리 정보와 Disparity와의 관계
  - 왼쪽 영상의 한 점의 위치에 비해 오른쪽 영상의 대응점 위치의 차이를 disparity라고 부르며, 그 관계식은 다음과 같다.
  - 얼마나 멀리 있느냐, 가까이 있느냐를 알 수 있음
  - 스테레오 카메라로 어떤 물체를 촬영해보면, 가까이에 있는 물체는 왼쪽 영상과 오른쪽 영상에 그 차이가 두드러지게 나타나고, 멀리있는 물체는 차이가 상대적으로 작게 나타난다.
  - 왼쪽 카메라와 오른쪽 카메라의 거리가 멀면 disparity도 크게 나타나기에 거리정보를 보다 정밀하게 파악할 수 있다.
- 이제 disparity를 계산하여 나온 거리정보에서 왼쪽 이미지의 한 점이 오른쪽 이미지 상 어디에 존재하는지를 찾아내야 한다. 이를 매칭 또는 correspondence라고 부른다.
- 문제는 해상도의 영상에서 거리를 추출하면서 계산되는 연산량이 늘어나면서 연산 시간도 늘어나게 된다.
- Disparity Map
  - 원본 이미지에서 모든 이미지 픽셀의 해당 지점을 식별하며, 왼쪽과 오른쪽 각각의 응답에 대한 쌍의 disparity를 계산한다.
  - 가까운 물체는 더 큰 차이를 나타내며, 맵은 disparity가 작을수록 어둡고, disparity가 클수록 밝다(카메라로부터 거리가 가깝다).
- Correspondence Problem
  - 왼쪽과 오른쪽 이미지가 어떻게 같은가가 중요
    1) Normalized Cross-Correlation(NCC)
    - template matching이란 입력으로 들어온 source image에서 원하는 template을 찾는 것을 말하는데, template image와 같은 사이즈의 window를 가지고 source image의 모든 subimage들과 비교하면서 유사도가 가장 높은 부분을 찾는다.
    - 그리고 이러한 크기가 같은 두 이미지 유사도를 구하는 방법 중 하나가 NCC이다.
    
    2) Sum of Squared Differences(SSD)
    - SSD의 가장 잘 알려진 예는 표준편차(standard deviation)이다.
    - 표준편차는 산포도의 일종으로 여러 값들이 평균으로부터 얼마나 떨어져있는지를 계량화한 것인데, “편차의 제곱”의 합을 도수로 나누어 계산한다.
    - 이처럼 여러 개의 관측값들이 평균으로부터 얼마나 떨어져있는지를 계량화하고자 할 때, sum of squares를 구한다.
    
    3) Structure From Motion(SFM)
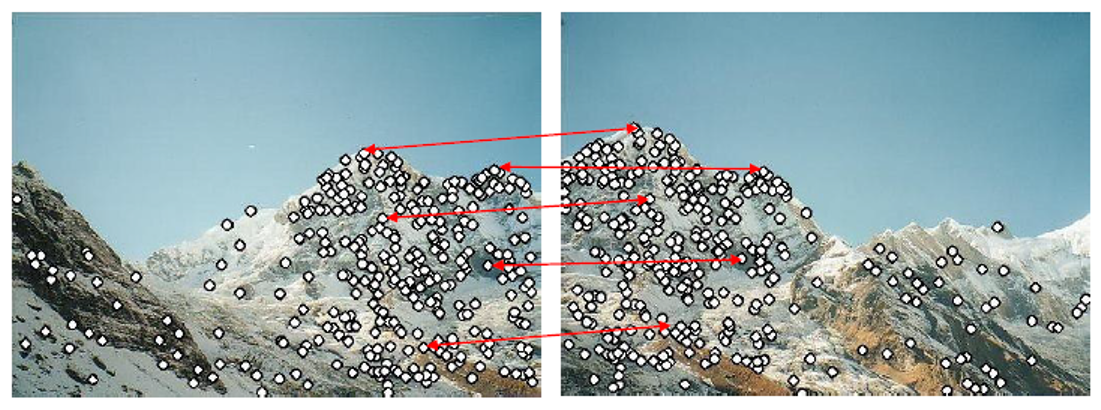
    - SFM은 2차원으로 촬영한 이미지의 모션정보를 이용해 촬영된 이미지의 카메라 위치와 방향을 역추적한 후 이미지들과 카메라들의 관계를 구조화하는 알고리즘이다.
    - SFM을 이용해, 각 촬영 이미지의 고유한 특징점(Feature Point)을 얻고 각 촬영 장면마다 특징점들과 관계를 서로 매칭하고 계산해 카메라의 위치를 얻을 수 있다.

6. Image Processing

이미지/영상 처리: 이미지/영상를 개선시키기 위해(enhance)
intensities(밝기값): 에너지에서 얻은 값들(각각의 화소가 가지는 값들)
- 이미지: intensities의 매트릭스 형태로 나타난다.
- 가로, 세로 사이즈가 이미지의 해상도
- 픽셀은 하나의 intensities를 담고 있는 것
- 픽셀의 개수가 resolution
- 1바이트로 표현함(0~255)
영상에서는 어떤 정보가 USEFUL, REDUNDANT 하는가?
- 값이 바뀌는(변화율이 큰) -> USEFUL
- intensities가 급격하게 바뀌는 지점이 고주파 성분이 바뀌는 지점
  -> 고주파 성분이 영상에서 중요한 정보(에지, 코너 등)
Image filtering(특정한 성분을 제거하거나 추출하는 작업)
1) Low pass: low frequency 성분만을 필터링
- 노이즈가 있는 경우(intensities에 너무 많은 노이즈가 껴있는 경우) 사용
- 픽셀에 대한 인텐시티브 값을 평균으로 만들어서 필터로 사용(스무딩) -> 영상이 blur 해질 수 있음
- 인텐시티브 값들을 순서대로 만들어서 중간값을 취하는 방법 -> 스무딩은 average를 추출

2) High pass: high frequency 성분만을 필터링
- 정보를 사용하기 위해서 사용
- 차이가 많이 나는 두드러진 부분만을 추출
- 엣지 성분이 주로 추출
spatial filter(공간상의 필터링)
- \(S_(xy)\)는 점 (x, y)를 중심으로 이미지의 이웃 픽셀의 영역으로, 필터링은 출력 이미지의 대응되는 픽셀의 새로운 값을 만들어내는 것이다.
- average filter는 마스크의 모든 필터를 합하여 평균을 내는 것
필터링 명령에 가장 기본적이 활용이 가능한 방법
- Correlation
  - 매칭(내가 원하는 샘플과 이미지에서 어디 부분이 일치하는지)
  - 얼마만큼 비슷한지
  - 큰 값일 수록 매칭이 높음
  - SSD(Sum of Squared Differences)라고 하는 에러를 제곱하여 최소화가 되도록
  - 가장 작은 값이 가장 닮아있는 위치
  - 차이가 너무 크면 안좋기 때문에 normalize할 수도 있다
    -> Filter 값에 I를 곱하는 것(Correlation) : 가장 정확히 매칭된 포인트들 끼리 합을 하는 것이 가장 큰 값을 가질 것임
    -> 절대값이 커지는 것이 correlation이 좋다고 할 수 있지만, 어느 경우에는 차이가 많이 나는 경우에도 절대값이 커지게 되어 일치하는 값보다 더 매칭이라고 할 수 있다(착각) -> 이를 해결
    => 지금 있는 템플릿과 현재 템플릿의 인텐시브 값을 노멀라이즈해서(0~1값) -> 코렐레이션 -> 베스트 매칭 -> 크기값을 노멀라이즈
  - 가우시안 분포를 따라 가우시안 값을 넣어준다.
- Convolution
  - correlation은 유사성 정도를 나타내는 함수라면, convolution은 하나의 함수와 또 다른 함수를 이용하여 새로운 함수를 구하는 함수이다.
Edge Detection
- 목표 - high pass filter 사용
- 한 방향으로 인텐시티 값이 불연속적인 값을 엣지라 함
- 엣지는 인텐시티가 급격하게 변하는 부분에 일치해서 만들어짐(검정이었다가 흰색으로 바뀌는 경계)
- 엣지는 인텐시티 차이값을 구해서 만들 수 있음
- 노이즈가 있는 경우에는 인텐시티의 차이가 너무 높아서 이걸 미분하게 되면 변화율이 너무 심한 상태가 되어버림
  -> 노이즈 필터링이 필요함(가우시안)
  -> 노이즈가 스무딩되면서 제거되고, 다시 필터를 적용
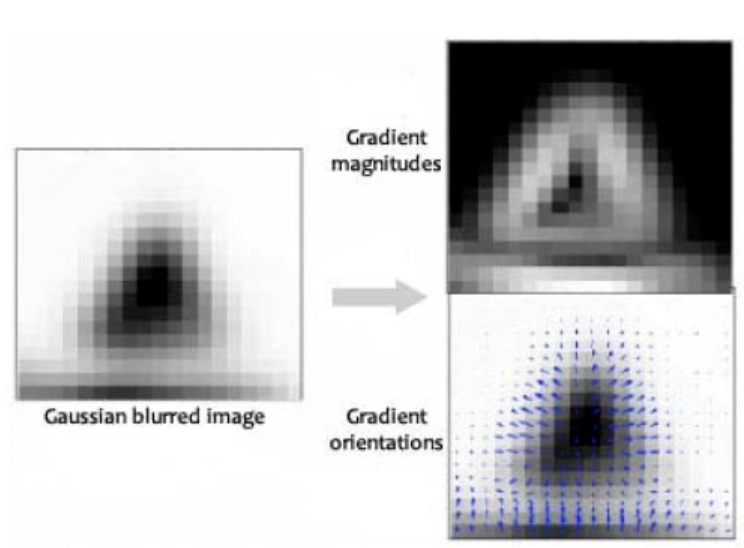
  -> 이러한 것을 동시에 할 수 있는 것이 가우시안 자체를 미분(gradient gaussian)
  -> 비대칭적인 성분인 경우에만 사용 가능
  -> LoG(라플라시안 of 가우시안)은 대칭적인 성분에서 사용 가능
- 엣지가 정말 필요하다면 엣지 부분을 바이너라이제이션 -> 비최대치 억제 알고리즘을 해서 엣지 성분만 추출 1) LOG를 통해 굵은 면처럼 생긴 선이 생김 2) 임계값을 통해 임계값보다 작으면 삭제 3) 비최대치 억제 알고리즘을 통해(finning 알고리즘) 엣지를 추출
이미지로부터 특징을 찾기
1) 엣지
2) 포인트(코너)
- SIFT, SURF, ORB(포인트에 대해서 구분이 가능하도록 해주는 구분자(디스크립터)가 필요
- 주변의 인텐시티브 값을 비교하면 포인트에 대해 정확히 구분이 가능할 수 있기 때문에)
3) 직선, 평면, 등
피처는 어디에 쓰이나?
1) 로봇 네비게이션
2) 오브젝트 인식
- 포인트 피처를 찾아서, 포이트 디스크립터로 또 다른 이미지의 디스크립터와 매칭 -> 유사도를 찾아서 두 이미지 간의 correspondence를 계산
3) 3D reconstruction
- 매칭을 통해 오버랩되는 포인트와 뎁스를 얻어 3차원 좌표계로 나타냄
4) Motion tracking
- 이동량을 계산
파라노마

1) 포인트 피처를 찾고

2) corresponding 쌍을 찾고

3) 각 페어를 이미지를 겹침
- 문제
  1) 한 영상에서는 추출이 되지만, 다른 영상에서는 추출이 안됨
  -> 어느 시점에서 어떻게 뽑히더라도 특징이 추출이 되어야만을 전제로!
2) 두 피처간의 코레스폰더스(같은지, 다른지)를 찾기 위해선 구분이 가능해야 함
-> 점만으로는 구분할 수 없기 때문에 신뢰성과 구분성이 있는 feature descriptor가 필요하다.
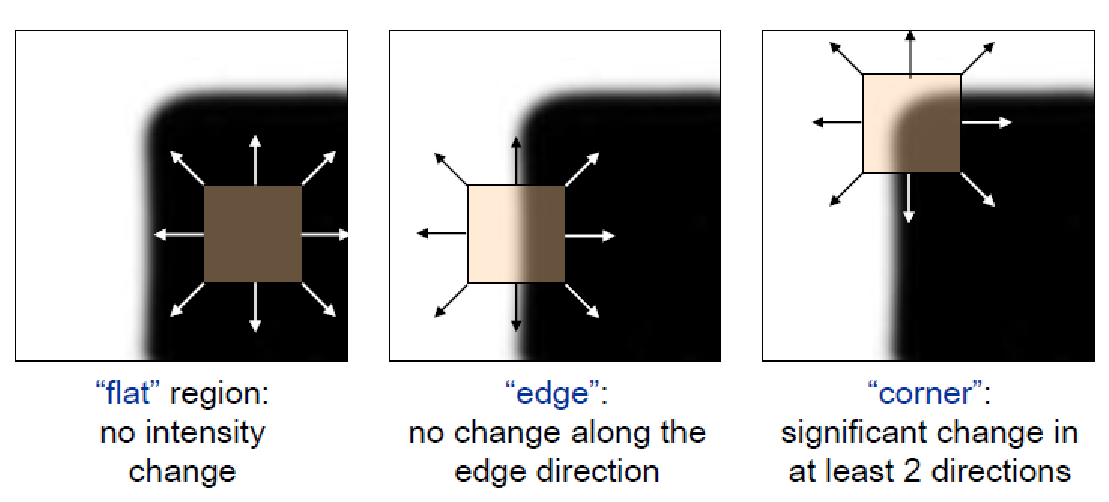
해리스 코너 검출
- 한 픽셀을 중심에 놓고 작은 윈도우(window)를 설정한 후에, 이 윈도우를 x축 방향으로 u만큼, y축 방향으로 v만큼 이동시킨다.
- 그 다음 윈도우 내의 픽셀값들의 차이의 제곱의 합을 구해준다.
- 이를 계산하여 픽셀값이 얼마나 변화했는지를 검출하여 코너점인지 아닌지를 판단한다.
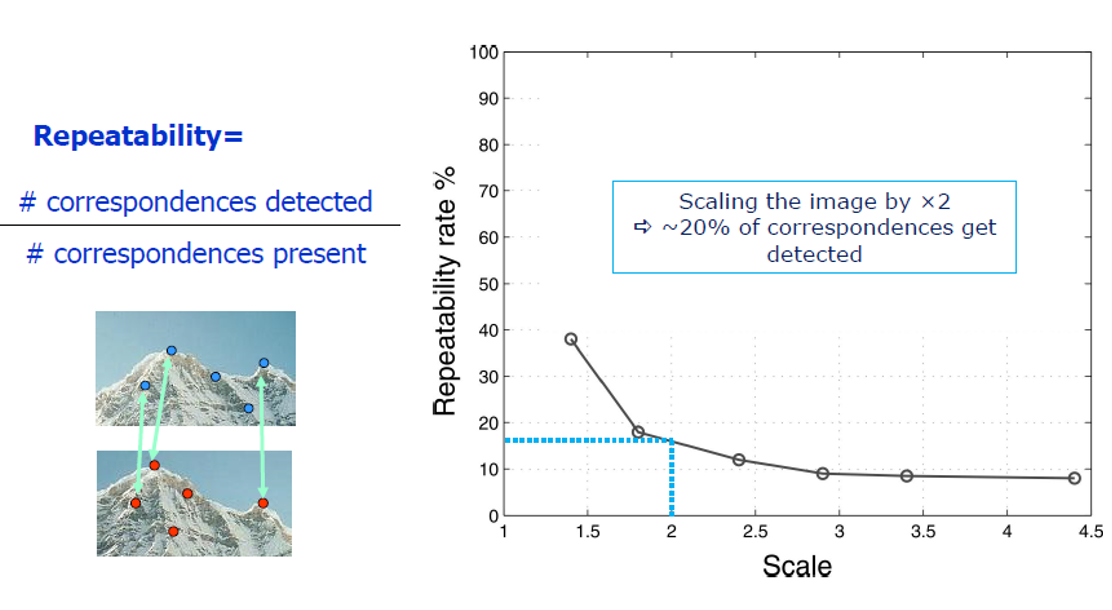
- 해리스 코너의 가장 큰 단점은 스케일이 달라지면, 코너가 달라진다. 이를 해결하기 위해 scale invariant detection을 이용하여 피처를 찾는다.
Scale Invariant Feature Transform(크기불변 이미지 특성 검출 기법)
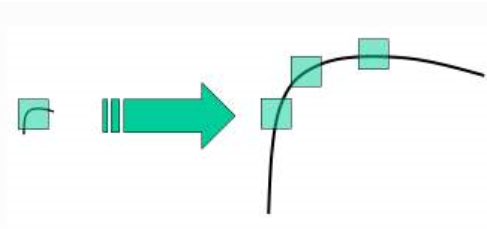
- 해리스 코너 검출은 이미지가 회전하더라도 코너를 제대로 검출할 수 있지만, 이미지의 크기가 커지면 코너를 제대로 검출하지 못한다.
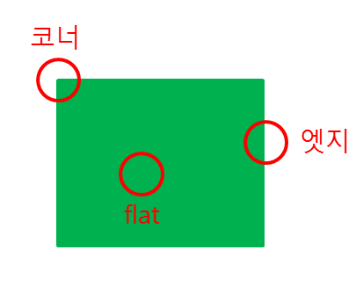
- 아래의 그림에서 이미지가 작을 때는 코너로 인식하지만, 부분을 확대하게 되면 평탄해지면서 코너로 인식하지 못하기 때문이다.
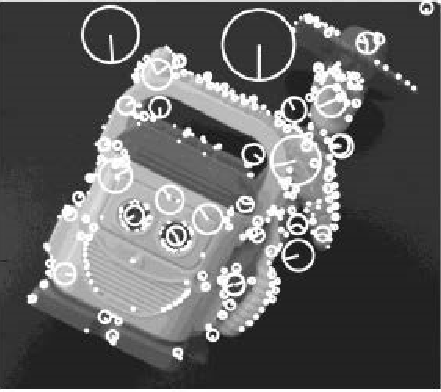
- SIFT 알고리즘은 이미지에서 스케일 불변인 키포인트를 추출하고, 추출한 키포인트들의 descriptor를 계산하는 것이다.
- 간단히 설명하자면, 이미지의 크기와 회전에 불변하는 특징을 추출하는 알고리즘으로, 서로 다른 두 이미지에서 SIFT 특징을 각각 추출한 다음에 서로 가장 비슷한 특징끼리 매칭해주면 두 이미지에서 대응되는 부분을 찾을 수 있다는 것이 기본 원리이다.
- SIFT 알고리즘의 주요 5단계 절차
  1) Scale-space Extrema Detection(스케일-공간 극값 검출)
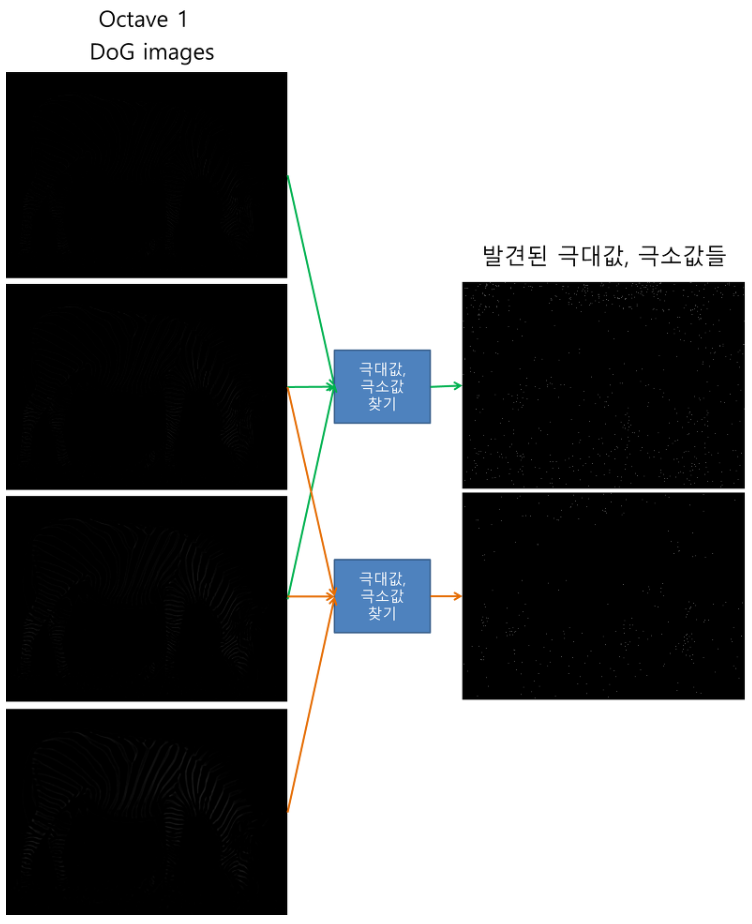
  - 가우시안 필터 후 라플라시안 필터(Laplacian of Gaussian, LoG)를 적용하면 이미지에서 다양한 크기의 이미지를 검출한다.
  - 하지만 LoG는 다소 시간이 소요되기 때문에 하나의 이미지에 서로 다른 필터를 적용한 가우시안 피라미드 이미지의 차이(Difference of Gaussian, DoG)를 이용한다.
  - DoG를 찾으면 이미지에서 스케일-공간 좌표상 극값을 찾는다. 이 극값을 잠재적 키포인트(Potential Keypoint)라고 한다.
  
  2) Keypoint Localization(키포인트 지역화)
  - 이미지에서 잠재적 키포인트들의 위치를 모두 찾았으면, 보다 정확한 결과를 위해 잠재적 키포인트들의 정제과정을 거쳐 키포인트들을 추출한다.
  - 테일러 전개를 이용해 수행한다.
  
  3) Orientation Assignment(방향 할당하기)
  - 최종적으로 추출된 키포인트들에 방향성-불변이 되도록 방향을 할당한다.
  - 즉, 이미지가 확대되거나 회전되더라도 추출된 키포인트들은 이미지의 특징을 고스란히 보존하게 된다.
  
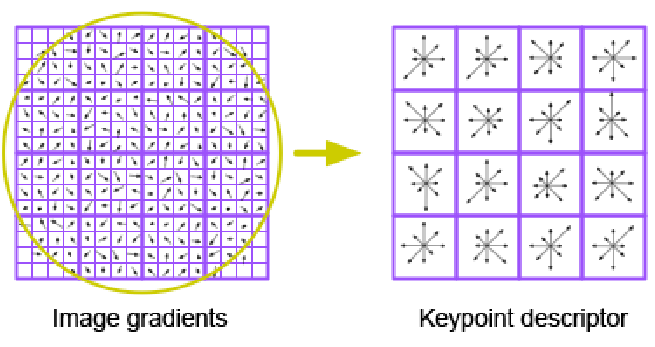
  4) Keypoint Descriptor(키포인트 디스크립터 계산하기)
  - 키포인트를 이용하여 키포인트 디스크립터를 계산한다.
  - 키포인트 디스크립터는 이미지 히스토그램을 활용하여 표현한다.
  - 이 외에 조명의 변화나 회전 등에도 키포인트들이 특징을 보존하기 위한 몇가지 측정값을 추가한다.
  
  5) Keypoint Matching(키포인트 매칭)
  - 두 개의 이미지에서 키포인트들을 매칭하여 동일한 이미지 추출이나 이미지 검색 등에 활용한다.