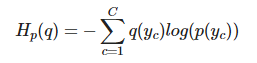Deep Learning Concept Theorem

Published On August 13, 2020

딥러닝 개념 정리

1. Parameter & Hyper Parameter

파라미터와 하이퍼 파라미터는 엄연히 차이가 있다.
Parameter
- Parameter는 매개변수로, 모델 내부에서 결정되는 변수이다.
- Neural Network에서 Perceptron 개념에서 등장하는 수식은 가중치(Weight)와 편향(bias)로 구성된다. 이때의 W와 b는 데이터를 통해 구해지며, 모델 내부적으로 결정되는 값으로 파라미터라고 한다.
- Parameter의 특징 1) 예측을 수행할 때, 모델에 의해 요구되어지는 값들이다.
  2) 모델의 능력을 결정한다.
  3) 측정되거나 데이터로부터 학습되어진다.
  4) 사용자에 의해 조정되지 않는다.
  5) 학습된 모델의 일부로 저장된다.
- Parameter의 예 1) 딥러닝에서의 Weight과 bias
  2) SVM에서의 서포트 벡터
  3) Linear Regression에서의 결정계수
Hyper Parameter
- Hyper Parameter는 모델링을 할 때, 사용자가 직접 설정해주는 값을 뜻한다.
- Neural Network에서 모델 훈련을 할 때 등장하는 다양한 개념인 learning rate가 있다.
- Hyper Parameter는 정해진 최적의 값이 없고, heuristics 방법이나 empirical하게 결정하는 경우가 많다.
- Hyper Parameter의 특징 1) 모델의 parameter값을 측정하기 위해 알고리즘 구현 과정에서 사용된다.
  2) Empirical하게 측정되기도 하며, 알고리즘을 여러 번 수행하면서 최적의 값을 구해나간다.
  3) 사용자에 의해 조정된다.
  4) 예측 알고리즘 모델링의 문제점을 위해 조절된다.
- Hyper Parameter의 예 1) 딥러닝에서의 learning rate, batch size, loss function 등
  2) SVM에서의 C
- Hyper Parameter의 최적화 방법 1) Manual Search
  + 사용자의 직감 또는 경험에 의해
  
  2) Grid Search
  + 처음부터 시작하여 모든 조합을 시행
  
  3) Random Search
  + 범위 내에서 무작위값을 반복적으로 추출
  
  4) Bayesian Optimization
  + 기존에 추출되어 평가된 결과를 바탕으로 추출 범위를 좁혀서 효율적으로 시행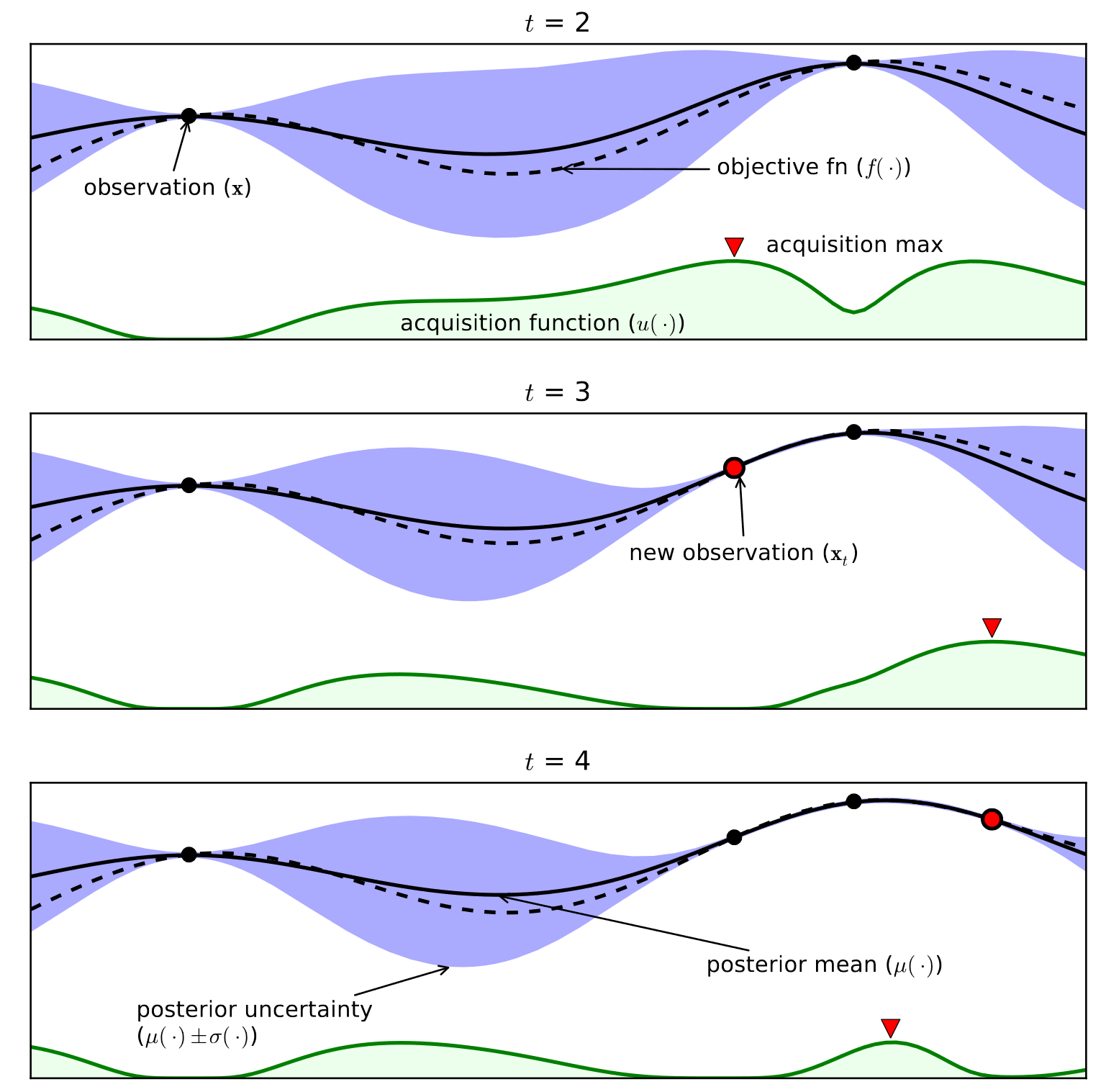

파라미터(Parameter)와 하이퍼 파라미터(Hyper parameter) Parameter vs HyperParameter 둘의 차이점은 무엇일까? Hyperparameter optimization

2. Loss Function

Loss Function은 Cost Function이라고도 한다.

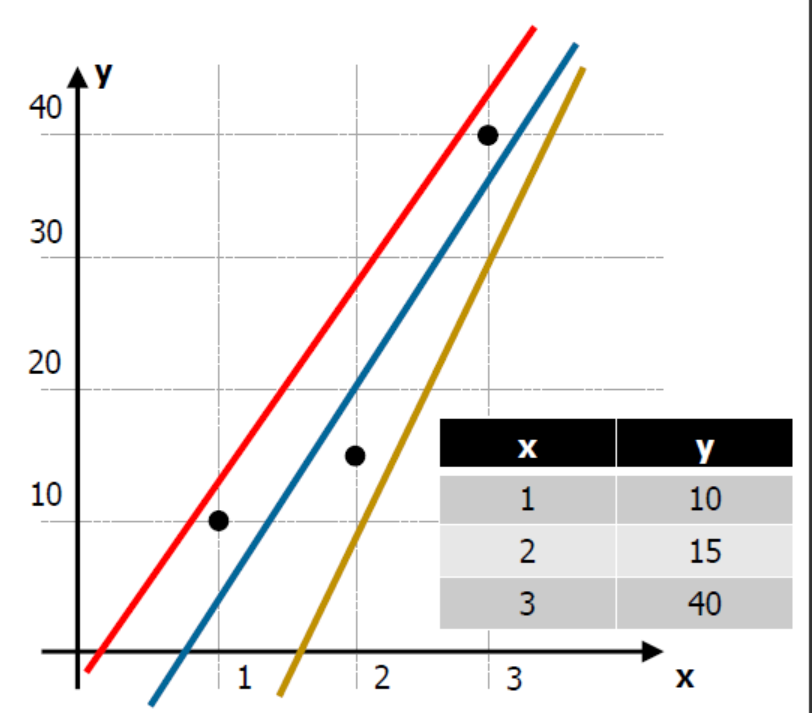
Loss Function은 어디서 사용되는 것일까? 예를 들어보자. 위의 사잔과 같이 3개의 직선 중 어느 직선이 가장 좋아보이는가? 아마도, 예측 측면이나 분류 측면 모두 가운데 파란색 선이 가장 좋아보인다고 할 수 있을 것이다. 따라서 우리는 파란색 선과 같이 점과 직선 사이의 거리가 최소한이 되는 새로운 직선을 계속해서 만들어내야 한다.

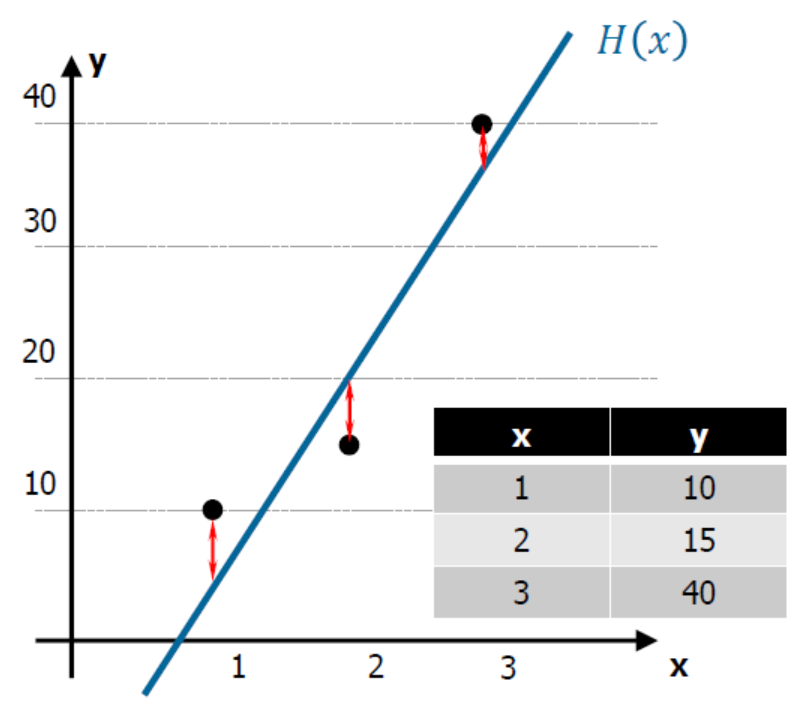
위의 사진과 같이 점과 직선 사이의 거리는 오차(cost, loss)라고 할 수 있으며, 손실 또는 비용함수를 만들 수 있다.

Loss Function의 종류 1) MSE(Mean Squared Error, 평균제곱오차) + 오차의 제곱에 대한 평균을 취한 값으로, 통계적 추정의 정확성에 대한 질적인 척도로 사용된다.

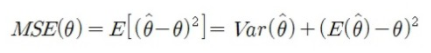
  + 예측값과 실제값의 차이가 클수록 MSE의 값도 커진다는 것은, 이 값이 작을수록 예측력이 좋다(추정의 정확성이 높아진다)고 할 수 있다.

  + 통계적으로 바라보는 MSE
      + 통계적 추정에 대한 설명

확률과 통계 챕터5. 표집분포와 통계적추론

      + 모집단에서 표본을 추출하여 각 표본 추정량의 값을 계산할 때 추정량이 바람직하기 위해서는 추정값들의 확률분포가 모수를 중심으로 밀집되어야 할 것이다.
          + 바람직한 추정량: 평균적으로 모수에 근접하고 그 밀집도가 높은 추정량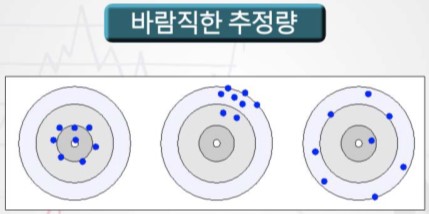

      + 이 밀집성의 정도는 MSE로 측정할 수 있다. 추정량($$\theta$$)과 추정모수($$\hat{\theta})와의 차이가 밀집성의 정도를 나타내는 지표로 사용할 수 있으며, 양의 값으로 취하기 위해서 제곱을 사용한다. 추정량은 일종의 확률변수이기 때문에 위에서 구한 차이의 제곱 역시 확률변수가 되기 때문에 이것의 평균을 구할 수 있으며, 그 결과를 평균제곱오차라고 한다.

      + MSE는 추정량 $$\hat{\theta}$$의 분산, 그리고 모수 $$theta$$와 추정량의 평균과의 편차 제곱에 의해 구성되므로, MSE값이 작은 바람직한 추정량이란 **$$\hat{\theta}$$의 평균이 가능한 한 $$\theta$$에 근접**하고 **분산도 동시에 작아야 함**을 의미한다.

      + 전자의 특성을 불편성(unbiasedness), 후자의 특성을 효율성(efficiency)이라 한다. 그리고 표본의 크기가 커질수록 MSE의 값이 감소하는 특성인 일치성(consistency)을 바람직한 추정량의 기준으로 고려한다.

2) Cross Entropy Error + entropy란 불확실성(uncertainty)에 대한 척도이다. 예측 모형으로 하려고 하는 것은 결국 불확실성을 제어하고자 하는 것이다. 만약 파란공만 들어가있는 가방에서 공을 뽑을 때의 불확실성은 0이다. 왜냐하면 결국 가방 안에는 모두 파란공만 들어있기 때문이다. 하지만 만약 빨간공과 파란공이 모두 들어가 있다면, 불확실성이 0보다 커질 수 밖에 없다. 즉, entropy는 예측하기 쉬운 일보다, 예측하기 힘든 일에서 더 높은 값을 가진다.

  + 예측 모형은 실제 분포인 q를 모르고, 모델링을 하여 q분포를 예측하고자 하는 것이다. 예측 모델링을 통해 구한 분포를 p(x)라고 하자. 실제 분포인 q를 예측하는 p분포를 만들었을 때, cross-entropy는 아래의 식과 같다.

  + 훈련 데이터를 사용한 예측 모형에서 cross-entropy는 실제값과 예측값의 차이를 계산하는데 사용할 수 있다.

추정의 이해(점추정, 평균제곱오차(MSE)) 통계학 개론 Cross-entropy 의 이해: 정보이론과의 관계

3. Optimization

5. Artificial Neural Networks(ANN)

4. Learning rate & Batch size

Learning rate
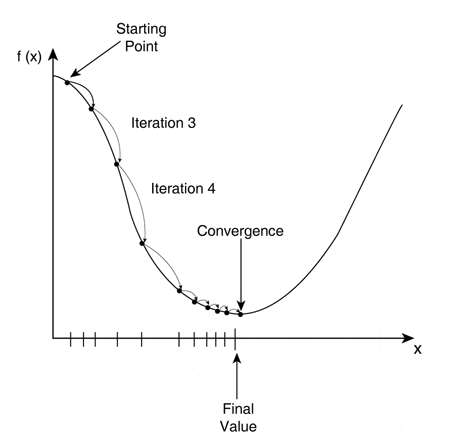
- Optimization에서 배운 GD 알고리즘에서 loss function이 최소가 되는 최적의 해를 구하는 과정에서, iteration을 수행할 때 다음 point를 어느 정도로 옮길지를 결정하는 것이 learning rate라고 한다.
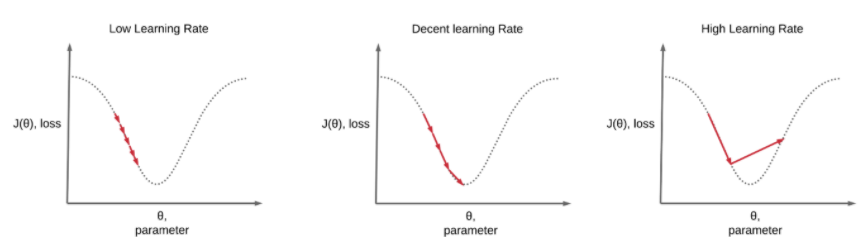
- learning rate를 설정할 때 주의해야 할 점은 1) learning rate가 너무 크게 되면, 최적의 값으로 수렴하지 않고 발산해버리는(overshooting) 경우가 발생한다.
  
  2) learning rate가 너무 작게 되면, 수렴하는 속도가 너무 느려 local minimum에 빠질 확률이 증가한다.
Learning Rate, Overfitting, Regularization Learning Rate Scheduling
Batch size
- batch size는 한 번의 batch마다 주는 데이터 샘플의 사이즈이다. 보통 mini-batch를 사용하여 데이터셋을 나누어 학습을 시켜준다.
- batch size의 양에 따라 비유를 해보자면, batch size가 작다면 조금씩 학습하기 때문에 한 번에 많이 학습하는 것보다는 메모리를 덜 잡아먹는다. 반대로 batch size가 크다면 작을 경우보다 안정적으로 학습할 수 있다. 일반적으로 batch size가 커질 수록 성능이 좋아지지만, 자신의 메모리 양에 따라 적절하게 크기를 정해줘야 한다.

5. Back Propagation

Neural Network에서 학습은 inpuy layer에서 output layer를 향해 순차적으로 학습하면서 Loss Function가 최소가 되도록 Weight을 계산하고 저장하는 것을 Forward Propagation이라고 한다. 하지만 한 번 Forward Propagation 했다고 출력값이 정확하기란 어려울 것이다.
따라서 Forward Propagation을 하면서 발생하는 오차를 줄일 필요가 있다. 이때 Loss Function이 최소값을 찾아가는 방법을 GD 알고리즘을 활용하며, 각 layer에서 가중치를 업데이트하기 위해서는 각 layer의 gradient를 계산해야 한다. gradient가 얼마나 변했는지를 계산하기 위해서는 변화량을 구해야 하는 것이므로 미분을 활용한다.
propagation이 한 번 돌리는 것을 1 epoch 주기라고 하며, epoch를 늘릴수록 가중치가 계속 업데이트되면서 점점 오차가 줄어나간다.

위의 그림을 보면 output layer에서 나온 결과값이 가진 오차가 0.6이고, 이전 노드 output layer에서 위의 노드와 아래 노드는 각각 3과 2를 전달해주고 있다. 이는 output error에 위의 노드와 아래 노드는 각각 60%, 40%의 영향을 주었다고 볼 수 있다. 균등하게 가중치를 나눠줄 수 있지만 영향을 더 준 노드가 의미가 더 있기 때문에 Back Propagation을 할 때도 영향을 준 크기만큼 비례하여 주는 것이 좋다. 이렇듯 Back Propagation은 오차를 점점 거슬러 올라가면서 다시 전파하는 것을 의미하며, 오차를 전파시키면서 각 layer의 가중치를 업데이트하고 최적의 학습 결과를 찾아가는 방법이다.
또한, Back Propagation은 chain rule을 사용하여 gradient의 계산과 업데이트를 엄청 간단하게 만들어주는 알고리즘으로, 각각의 parameter의 gradient를 계산할 때 parallelization도 용이하고, 메모리도 아낄 수 있다.
- Chain Rule
  - 1) x가 변화했을 때 함수 g가 얼마나 변하는지
  - 2) 함수 g의 변화로 인해 함수 f가 얼마나 변하는지
  - 3) 함수 f의 인자가 함수 g이면 최종값 F의 변화량에 기여하는 각 함수 f와 g의 기여도가 어떤지

순전파(forward propagation), 역전파(back propagation) 오차 역전파, 경사하강법 Machine Learning 스터디 (18) Neural Network Introduction [Deep Learning이란 무엇인가?] Backpropagation, 역전파 알아보기 What is backpropagation really doing? | Deep learning, chapter 3

Tags: DeepLearning